SECTION I (50 marks)
Answer all questions in this section in the spaces provided.
- The length and width of a rectangular piece of paper were measured as 60 cm and 12 cm respectively. Determine the relative error in the calculation of its area. (4 marks)
- Simplify
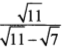 (2 marks)
(2 marks) - An arc 11 cm long, subtends an angle of 700 at the centre of a circle. Calculate the length, correct to one decimal place, of a chord that subtends an angle of 900 at the centre of the same circle. (4 marks)
- In the figure below, O is the centre of a circle. A, B, C and D are points on the circumference of the circle. Line AB is parallel to line DC and angle ADC = 550.
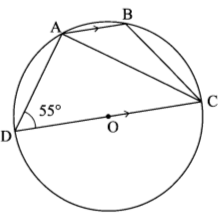
Determine the size of angle ACB. (3 marks) - Eleven people can complete ⅗ of a certain job in 24 hours. Determine time in hours, correct to 2 decimal places, that 7 people working at the same rate can take to complete the remaining job. (3 marks)
- The length and width of a rectangular signboard are (3x + 12) cm and (x - 4) cm respectively. If the diagonal of the sign post is 200 cm, determine its area. (4 marks)
- Find the value of x given that log (x - 1) + 2 = log (3x + 2) + log 25 (3 marks)
- Use the expansion of (x - y)5 to evaluate (9.8)5 correct to 4 decimal places. (3 marks)
- The diameter of a circle, centre O has its end points at M (-1, 6) and N(5, -2). Find the equation of the circle in the form x2 + y2 +ax + by = c where a, b and c are constants. (4 marks)
- Below is a line AB and a point X. Determine the locus of point P equidistant from point A and B and 4 cm from point X. (3 marks)

- In a nomination for a committee, two people were to be selected at random from a group of 3 men and 5 women. Find the probability that a man and a woman were selected. (2 marks)
- A school decided to buy at least 32 bags of maize and beans. The number of bags of maize were to be more than 20 and the number of bags of beans were to be at least 6. A bag of maize costs Ksh 2500 and a bag of beans costs Ksh 3500. The school had Ksh 100 000 to purchase the maize and beans. Write down all the inequalities that satisfy the above information. (4 marks)
- Evaluate
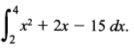 . (2 marks)
. (2 marks) - The position of two points P and Q, on the surface of the earth are P(450N, 360E) and Q(450N, 710E). Calculate the distance, in nautical miles, between P and Q, correct to one decimal place. (3 marks)
- Solve the equation sin(½x - 300) = cos x for 0 < x < 900 (2 marks)
- The position of vector points P,Q and R are OP = (-36), OQ = (-21), OP = (4-1). Show that P, Q and R are collinear. (3 marks)
SECTION II (50 marks)
Answer any five questions in this section in the spaces provided. - In a retail shop, the marked price of a cooker was Ksh 36 000. Wanandi bought the cooker on hire purchase terms. She paid Ksh 6400 as deposit followed by 20 equal monthly instalments of Ksh 1750.
- Calculate:
- The total amount of money she paid for the cooker. (2 marks)
- The extra amount of money she paid above the marked price. (1 mark)
- The total amount of money paid on hire purchase terms was calculated at a compound interest rate on the marked price for 20 months. Determine the rate, per anum, of the compound interest correct to 1 decimal place. (4 marks)
- Kaloki borrowed Ksh 36 000 from a financial institution to purchase a similar cooker. The financial institution charged a compound interest rate equal to the rate in (b) above for 24 months. Calculate the interest Kaloki paid correct to the nearest shilling. (3 marks)
- Calculate:
- Mute cycled to raise funds for a charitable organisation. On the first day, he cycled 40 km. For the first 10 days, he cycled 3 km less on each subsequent day. Thereafter he cycled 2 km less on each subsequent day.
- Calculate:
- The distance cycled on the 10th day; (2 marks)
- The distance cycled on the 16th day. (3 marks)
- If Mute raised Ksh 200 per km, calculate the amount of money he collected. (5 marks)
- Calculate:
- The equation of a curve is given by y = 1 + 3 sin x.
- Complete the table below for y = 1 + 3 sin x correct to 1 decimal place. (2 marks)

-
- On the grid provided, draw the graph of y = 1 + 3 sin x for 0 (3 marks)

- State the amplitude of the curve y = 1 + 3 sin x. (1 mark)
- On the grid provided, draw the graph of y = 1 + 3 sin x for 0 (3 marks)
- On the same grid draw the graph of y = tan x for 900 ≤ x ≤ 2700 (3 marks)
- Use the graphs to solve the equation 1 + 3 sin x = tan x for 900 ≤ x ≤ 2700(1 mark)
- Complete the table below for y = 1 + 3 sin x correct to 1 decimal place. (2 marks)
- The figure below represents a cuboid EFGHJKLM in which EF = 40 cm, FG = 9 cm and GM = 30 cm. N is the midpoint of LM.
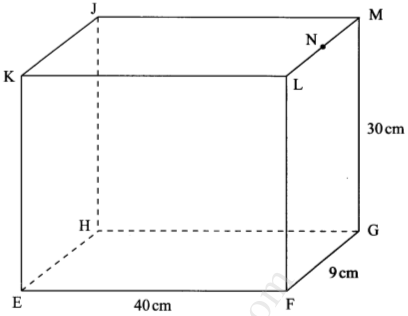
Calculate correct to 4 significant figures:- The length of GL; (1 mark)
- The length of FJ; (2 marks)
- The angle between EM and the plane EFGH; (3 marks)
- The angles between planes EFGH and ENH; ( 2 marks)
- The angle between lines EH and GL. (2 marks)
- A quantity P varies partly as the square of m and partly as n. When P = 3.8, m = 2 and n = -3. When P = -0.2, m = 3 and n = 2.
- Find:
- The equation that connects P,m and n; (4 marks)
- The value of P when m =10 and n = 4. (1 mark)
- Express m in terms of P and n. (2 marks)
- If P and n are increased by 10%, find the percentage increase in m correct to 2 decimal places. (3 marks)
- Find:
- A particle was moving along a straight line. The acceleration of the partcle after t seconds was given by (9 - 3t) ms-2. The initial velocity of the particle was 7ms-1.
Find:- The velocity (v) of the particle at any given time(t); (4 marks)
- The maximum velocity of the particle; ( 3 marks)
- The distance covered by the particle the time it attained maximum velocity. (3 marks)
- The marks scored by 40 students in a mathematics test were as shown in the table below.

- Find the lower class boundary of the modal class. (1 mark)
- Using an assumed mean of 64, calculate the mean mark. (3 marks)
-
- On the grid provided, draw the cumulative frequency curve for the data. (3 marks)

- Use the graph to estimate the semi-interquartile range. (3 marks)
- On the grid provided, draw the cumulative frequency curve for the data. (3 marks)
- A quadrilateral with vertices at K(1, 1), L(4, 1), M(2, 3) and N(1, 3) is transformed by a matrix T = (10 31)to a quadrilateral K', L', M',N'
- Determine the coordinates of the image. (3 marks)
- On the grid provided draw the object and the image. (2 marks)

-
- Describe fully the transformation which maps KLMN onto K'L'M'N'. (2 marks)
- Describe the area of the image. (1 mark)
- Find a matrix which maps K'L'M'N' onto KLMN. ( 2 marks)

MARKING SCHEME
- Actual area = 60 x 12
= 720 cm2
Absolute error
= ½[(60.5 x 12.5)-(59.5x11.5))
= 36
Relative error = 36
720
= 0.05 - √11 = √11 -√11 +√7
(√11+7) 7 (√11 - √7)(√11 +√7)
11 + √77
4
M1 Rationalizing denominator - 7 x 2 x r x 22 = 11
360 7
r = 11x 360 x 7
2 x 22 x 70
= 9
Length of chord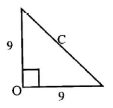
C = √92 +92
MI Or equivalent
= 12.7 - Angle ACD = 180 - (90 + 55)
= 35°
Angle ACB = 180 - (90 + 35 + 35)
= 20° - 1 person takes 24 x 11 = 264 h to do 3/5 of the job.
In 1 hour one person does 1 x 3 = 3
264 5 1320
7 persons can do 3 x 7 Bizo of the job in 1 hour
1320
Time 7 persons take to complete 2/5 of the job = 2/5 x 1320
21
= 25.14 hours - (3x + 12)2 + (x - 4)2 = 2002
9x2 + 72x + 144 + x2 - 8x + 16 = 40000
10x2 + 64x - 39840 = 0
(x - 60)(5x + 332) = 0
X = 60
Area = 56 x 192 = 10752 cm2 - Log (x - 1) + log 100 = log (3x + 2) + log 25
Log 100(x - 1) = Log 25 (3x + 2)
(x - 1)100 = (3x + 2) 25
100x - 100 = 75x + 50
25x = 150
x = 6 - (x - y)5 = x5 - 5x4y + 10x2y2 + 5xy4 - y5
9.85 = (10 -0.2)5
= 105 - 5(10)4 x 0.2 + 103 x 0.2
10 X 102 x 0.23 + 5 x 10 x 0.24 - 0.25
= 90392.0797 - Centre of circle =(-1 + 5, 6 + -2)
2 2
= (2,2)
Radius = √(-1 – 5)2+(6+2)2
2
√36 +64 = 5
2
Equation of circle =
(x - 2)2 + (y - 2)2 = 52
x2 - 4x + 4 + y2 - 4y + 4 = 25
x2 + y2 - 4x - 4y = 17 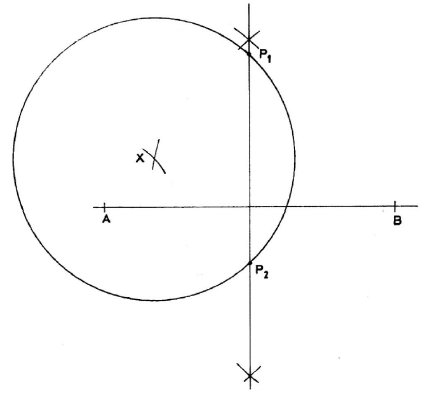
ar bisector of AB
Drawing circle centre x, radius 4 cm
Locating P1, and P2, (P1 P2 = 6 ± 0.1 cm)- 3 x 5 + 5 x 3
8 7 7 7
= 15
28 - m+b ≥ 32
m> 20
b≥6
2500 m + 3500 b ≤ 100000
5m + 76 ≤ 200 -
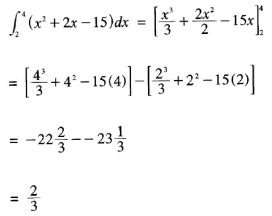
- Longitude difference = 71 - 36 = 35°
Distance in nautical miles
= 35 x 60 cos 45º
= 1484.9 nm - sin (½x-30) = sin (90 - x)
½x -30 = 90 - x
x = 80° 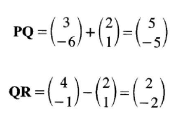
PQ = 5/2 QR and Q is a common point
P, Q and R are collinear-
-
- 6400+ 1750 x 20
= Ksh 41 400 - 41 400 - 36 000 = Ksh 5400
- 6400+ 1750 x 20
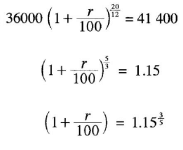
r = 0.087473554
100
r = 8.7473554
≈8.7%- 36000 x 1.0872
= 42536.484
42536.484 - 36000
= 6536.484
≈ Ksh 6536
-
-
-
- 40+ (10-1) (-3)
= 40-27 = 13 km - First term after 10 days
= 13 - 2 = 11
16th day: 11 + 5 x -2
= 1 km
- 40+ (10-1) (-3)
- S10 = 10 (2 x 40 + 9x -3)
2
= 5(80 - 27) = 265
S6 = 6 (2 x 11 + 5x - 2)
2
= 3(22 - 10) = 36
Total distance travelled
= 265+ 36 = 301
Amount of money raised
=Ksh 301 x 200
= Ksh 60 200
-
-
B2 Allow B1 for at least 57x° 0° 30° 60° 90° 120° 150° 180° 210° 240° 270° 300° 330° 360° y = 1 + 3sin x 1 2.5 3.6 4 3.6 2.5 1 -0.5 -1.6 -2 -1.6 -0.5 1 -
-
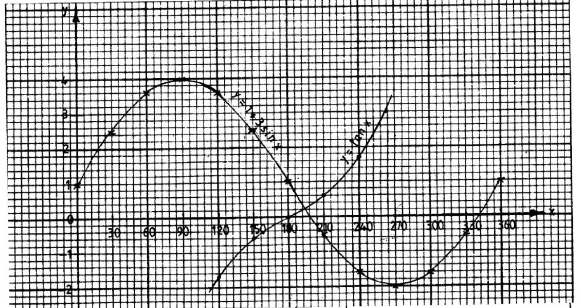
- Amplitude of curve = 3
-
- tan x values
Plotting y = tan xx 90 120 150 180 210 240 270 tan x -1.7 -0.6 0 0.6 1.7
tan r curve - 1 + 3 sin x = tan x
x = 195°
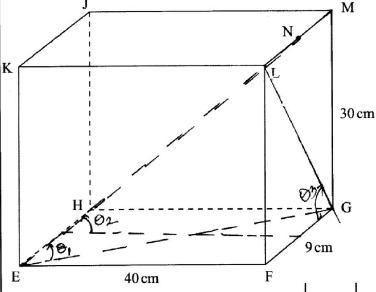
- Length GL = √30° +92 = 31.32
- Length FJ = √412 + 900
= 50.80 - angle between EM and plane EFGH
EG = √402 + 92 = 41
θ1 = tan-1 30
41
= 36.19° - angle between the plane EFGH and ENH
θ2= tan-1 30
40
= 36.87° - angle between lines EH and plane GL
= angle between lines FG and GL
θ3= tan-1 30
9
= 73.30°
-
-
- P=k1m2+ k2n
4k1 + - 3k2 = 3.8
9k1 + 2k2 = -0.2
8k1 - 6k2= 7.6
27k1 + 6k2= -0.6
35k1 = 7.0
k1 = 0.2
k1 = -1
P = 0.2m2 - n
MI Attempt to solve - P= 0.2 x 102 - 4 = 16
- P=k1m2+ k2n
- 0.2 m2 = P+n
m= √P+n
0.2 - New m = √1.1(P + n)
0.2
% increase in m = (√1.1 -1)√P+n
0.2 x 100
√P+n
0.2
= 4.88%
-
-
- V in terms of t
a = dV = 9-31 = V = ∫(9-31) dt
dt
V = 9t - 3t 2 + C
2
when t = 0, V = 7 - C=7
V = 9t – 3t 2 + 7
2 - maximum velocity
→ a = 9 - 3t = 0 t = 3
V = 9 x 3 – 3 x 9 +7
2
= 27 - 27 +7
2
= 34 - 13.5
= 20.5 ms-1 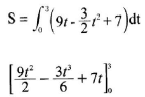
[81 - 3 x 27 + 21] – [0]
2 6
= 27+21
= 48 m
- V in terms of t
-
- Lower class boundary of modal class
62.5 - Mean mark:
Σfd = -42 +-36 +-40 + 12 +48 +33
= -25
mean = 64 - 25
40
= 63.375 -
-
BI for c.fCummulative frequency 3 7 17 29 37 40 Upper class boundary 52.5 57.5 62.5 67.5 72.5 77.5 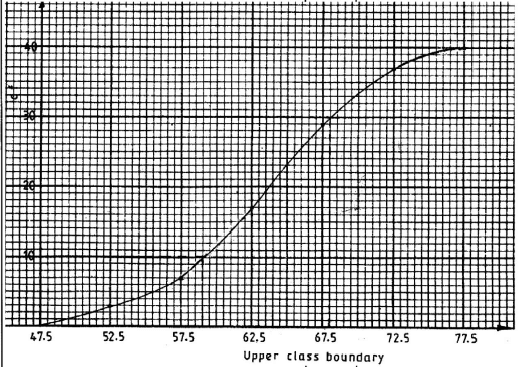
- Q3 = 68 ± 0.5
Q1 = 59 ± 0.5
Semi-interquartile range
= 68–59
2
= 4.5
-
- Lower class boundary of modal class
-
-
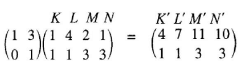
coordinates
K' (4,1), L' (7,1), M' (11,3), N' (10,3) 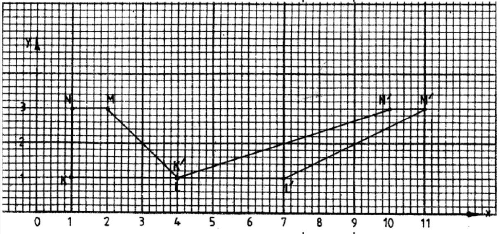
-
- shear with x axis (y = 0) invariant and point N(1,3), mapped onto N'(10,3)
any other point and its image may be used - area of image
=(3+1) x 2 =4
2
- shear with x axis (y = 0) invariant and point N(1,3), mapped onto N'(10,3)
-
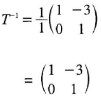
-
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download KCSE 2015 Mathematics Alt A Paper 2 with Marking Scheme.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

