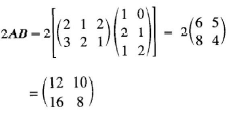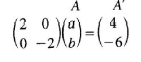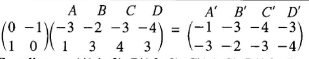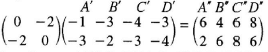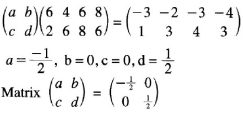SECTION I (50 marks)
Answer all the questions in this section in the spaces provided.
- Use a calculator to evaluate (3.84)2 - √110.592
0.03885 (2 marks)
- In a certain year, Ondege's annual salary was Ksh 120600. For the next seven years, his annual increment was Ksh 2 880.
Determine:
- Ondege's annual salary in the 7th year; (2 marks)
- the total salary that Ondege earned during the first six years. (2 marks)
- A curve crosses the x-axis at x = 11/3 and x = -½. Determine the equation of the curve in the form ax2 + bx + c = 0 where a, b and e are integers. (2 marks)
- Sifa invested an amount of money in a financial institution which paid a simple interest rate of 5% per annum. After 3½ years, the total amount of money in Sifa's account was Ksh 37 600. Calculate the amount of money that Sifa invested. (3 marks)
- A county allocated funds for various projects as shown in the pie-chart below.
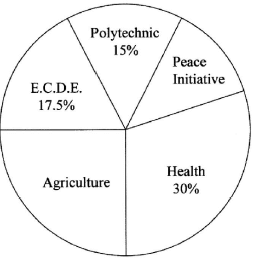
The allocation for Agriculture was twice that of Peace Initiative. Calculate the size of the angle of the sector that represents the Peace Initiative.
- Given that matrix
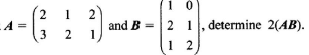 (3 marks)
(3 marks)
- The table below shows the amount of milk, in litres, delivered to a milk processing plant, on a certain day, by 80 farmers.
| Milk in litres |
10-14 |
15-19 |
20-24 |
25-29 |
30-34 |
35-39 |
40-44 |
45-49 |
| No. of farmers |
2 |
6 |
14 |
24 |
13 |
10 |
8 |
3 |
Estimate, by calculation, the median. (3 marks)
- A point A is mapped onto A'(4, -6) by a transformation whose matrix is
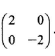
Find the co-ordinates of A. (3 marks)
- In a children's home, the amount of water in litres (L) used per month is partly constant and partly varies with the number n, of the children. In a certain month, there were 50 children and the amount of water used was 78 000 L. In another month, there were 70 children and 85 200 L of water was used.
- Form an equation connecting L and n. (1 mark)
- Determine the amount of water used in a month when the number of children was 100. (3marks)
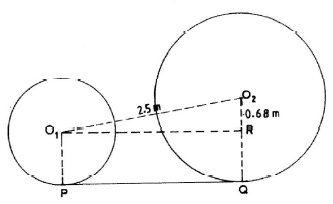
- The figure below shows two circles, centres O1 and O2. PQ is a common tangent to the circles. The radius of the smaller circle is 0.12m while the radius of the larger circle is 0.8 m. The distance between O1 and O2 is 2.5 m.
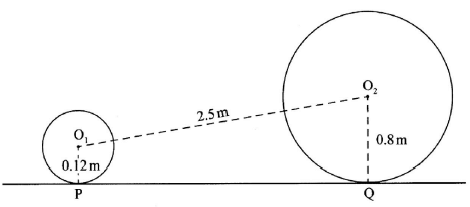
Calculate the length PQ, correct to 2 decimal places. (3 marks)
- T and R are two towns on the equator. The longitude of T is 12°E and that of R is 5°W. If the local time at T is 2245 h, find the time at R in the 12-hour clock system. (4 marks)
- Given that 4 tan x - 5 = 0, find the value of x correct to 2 decimal places for 0° ≤ x ≤ 360°. (3 marks)
- A box contains 13 balls which are identical except for the colour. Three of the balls are red while the rest are white. Two balls are picked at random from the box, one at a time, without replacement.
- Using a tree diagram, show all the possible outcomes. (2 marks)
- Find the probability that a red and a white ball are picked. (2 marks)
- The x and y values of points on a curve are as shown in the table below.
| x |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
| y |
1 |
3 |
6 |
10 |
15 |
21 |
Using the trapezium rule, estimate the area bounded by the curve, the x-axis and the lines x = 0.5 and x = 3. (3 marks)
- Points P, Q and R lie on a straight line, such that PQ = iPR. Given P(2,5) and R(6,1), express in terms of i and j:
- the position vector of P; (1 mark)
- PQ. (2 marks)
- In an experiment, water was heated and its temperature changes recorded at intervals of 2 minutes as shown in the table below.
| Time (min) |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
| Temperature (°C) |
25 |
35 |
42.5 |
50 |
60 |
67.5 |
77.5 |
85 |
92.5 |
- On the grid provided, plot the points and draw the line of best fit. (2 marks)
- Use the line of best fit to estimate the time taken for the temperature of the water to reach 75°C. (1 mark)
SECTION II (50 marks)
Answer any five questions from this section in the spaces provided.
- A factory blends three types of juice in the ratios A:B = 3:4 and B:C = 1:2.
- Determine:
- the ratio A:B:C; (1 mark)
- the amount of type A juice in a 20-litre mixture. (2 marks)
- The cost of producing one litre of A is Ksh 80, one litre of B is Ksh 84 and one litre of C is Ksh 90.
- Find the cost of producing one litre of the mixture. (2 marks)
- Calculate the selling price of one litre of the mixture if the factory makes a profit of 25%. (2 marks)
- The factory uses two types of machines P and Q to blend the juices. Machine P takes 7 hours to blend 14 000 litres and Q takes 5 hours to blend 12 000 litres. Determine the time it would take the factory to blend 550 000 litres. (3 marks)
- The diagram below represents a map of a settlement scheme. The map is drawn on a one centimetre square grid. The scale of the map is 1:50000
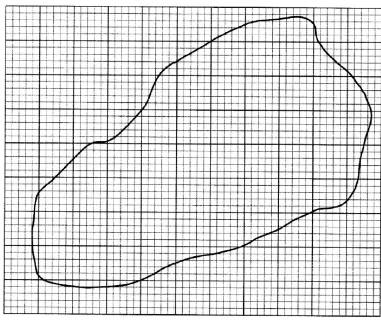
- Estimate:
- the area of the map in square centimetres; (2 marks)
- the area of the settlement scheme in square kilometres. (3 marks)
- The settlement scheme was sub-divided into parcels of land each of 5 hectares.
- Find the number of the 5 hectare parcels of land obtained. (3 marks)
- Determine the area in hectares of the settlement scheme that remained after the sub-division. (2 marks)
- In the figure below, TD is a tangent to the circle at T. Chord AC produced intersects TD at D. CD = 4.1 cm, TD = 7 cm and angle TAC = 33°.
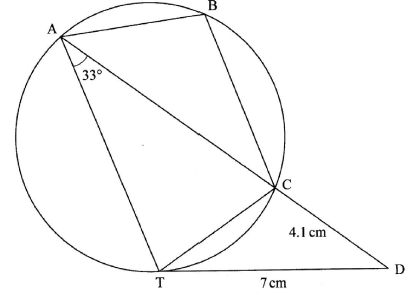
- Giving a reason, find the size of angle CTD. (2 marks)
- Calculate the length of AC correct to one decimal place. (3 marks)
- Calculate to the nearest degree the value of:
- the obtuse angle TCD; (3 marks)
- angle ABC. (2 marks)
-
- Complete the table below for values of y = x3 + 3x2 + 5 for -4 ≤ x ≤ 2, correct to 1 decimal place. (2 marks)
| x |
-4 |
-3.5 |
-3 |
-2.5 |
-2 |
-1.5 |
-1 |
-0.5 |
0 |
0.5 |
1 |
1.5 |
2 |
| y |
|
-1.1 |
5 |
|
9 |
|
|
5.6 |
|
5.9 |
|
15.1 |
|
- On the grid provided, draw the graph of y = x3 + 32 + 5 for -4 ≤ x ≤ 2. Use the scale: 2cm for 1 unit on the x-axis and 2cm for 5 units on the y axis. (3 marks)
- Using the graph, determine:
- the average rate of change between x = 0.5 and x = 1.8; (2 marks)
- the instantaneous rate of change of the curve at x = —3, correct to one decimal place. (3 marks)
- A pavement is of length (x - 1)m and width (x - 8)m. The area of the pavement is 4.56 m2.
-
- Write a quadratic equation for the area of the pavement in the form ax2 + bx + c = 0 where a, b and c are constants. (2 marks)
- Using the method of completing the square, find the actual length and width of the pavement. (6 marks)
- The pavement is covered with rectangular tiles measuring 0.4 m by 0.3 m. Determine the number of tiles used to cover the pavement completely. (2 marks)
- Omari bought a house valued for Ksh 4 000 000. The value of the house appreciated at 20% per annum for the first three years and then at 15% per annum for the next two years.
- Calculate the value of the house after:
- three years, (2 marks)
- five years. (2 marks)
- After the five years, the value of the house depreciated for the next two years. At the end of the two years, Omari sold the house through an agent. Omari received Ksh 7 125 000 after paying a 5% commission to the agent.
Calculate:
- the value of the house after the two years; (2 marks)
- the annual rate of depreciation in the two years. (4 marks)
- A quadrilateral ABCD has vertices A(-3, 1), B(-2, 3), C(-3, 4) and D(-4, 3).
-
- Find the co-ordinates of A'B'C'D', the image of ABCD, under a transformation whose matrix is
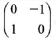 (2 marks)
(2 marks)
- On the grid provided, draw the quadrilateral ABCD and its image A'B'C'D'. (2 marks)
- A"B"C"D" is the image of A'B'C'D' under a transformation whose matrix is
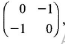 followed by an enlargement scale factor 2, centre (0,0).
followed by an enlargement scale factor 2, centre (0,0).
- Determine the co-ordinates of A"B"C"D". (2 marks)
- On the same grid as in (a) (ii) above, draw A"B"C"D". (1 mark)
- Find a single transformation matrix that maps A"B"C"D" onto ABCD. (3 marks)
- The masses, to the nearest kg, of 65 patients who attended a medical clinic are as shown in the table below:
| Mass (kg) |
26-30 |
31-35 |
36-40 |
41-45 |
46-50 |
51-55 |
| Frequency (f) |
9 |
13 |
20 |
15 |
6 |
2 |
Calculate:
- the mean mass of the patients; (4 marks)
-
- the variance mass; (5 marks)
- the standard deviation. (1 mark)

MARKING SCHEME
- 3.842 - 3√110.592
0.03885
14.7456 - 4.8
0.03885
= 256
B1 Squaring and cube roo
-
- Annual salary in the 7th year:
= 120 600 + 2880 x 6
= Ksh137 880
- Total earnings for 6 years
S6 = 6/2 {2 x 120 600 + 5(2880)}
= Ksh 766 800
- (x - 4/3)(x+½) = 0
x3 - 5/6x - 2/3 =0
6x2 - 5x -4 = 0
- P + PRT = 37600
100
P + P x 5 x 3.5 = 37600
100
P(1.175) = 37600
P = 37600
1.175
= Ksh 32 000
- 3x = 100 - (17.5 + 15 + 30)
x = 12.5%
Angle for peace initiative
= 12.5 x 360
100
= 45°
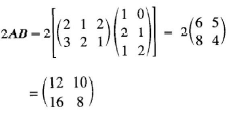
Multiplication by scalar
| Classes |
10-14 |
15-19 |
20-24 |
25-29 |
30-34 |
35-39 |
40-44 |
45-49 |
| frequency (f) |
2 |
6 |
14 |
24 |
13 |
10 |
8 |
3 |
| c.f |
2 |
8 |
22 |
46 |
59 |
69 |
77 |
80 |
cumulative frequency
Median = 24.5+ 40 - 22 x 5
24
= 24.5 +3.75
= 28.25
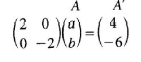
2a = 4 = a = 2
-2b = -6 b = 3
Coordinates of A=(2,3)-
- L=C+ an
- 78 000 = C + 50a
85 200 = C +70a
20a = 7200
a = 360
A1 For both C and a
C = 78 000 - 50 X 360
= 60 000
L = 60 000 + 100 x 360
= 96 000
- O2R = 0.8 -0.12 = 0.68
PQ = √2.52 -0.682
= 2.41
- Difference in longitude = 12° +5 = 17°
Time difference = 17 x 4
= 68 minutes
Time at R:
= 2245 h - 1 hr 08 min = 2137 h = 9.37 pm
- 4 tan x = 5
tan x = 5/4 = 1.25
x = tan -1 (1.25)
= 51.34°
and 231.34°
-
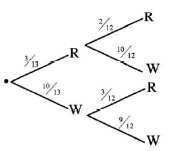
B1 for 1st branch correct
B1 for 2nd branch correct- P(R+W)
= 3 x 10 + 10 x 3
13 12 13 12
= 5
13
- Area
½ x ½[1+21+2(3+6+10+15)]
= ¼[22 +2 x 34] = 225
-
- OP = 2i + 5j
- PQ = 3/4 {(6i+j)-(21 – 5j)}
= 3/4 (4i - 4j)
=3i - 3j
-
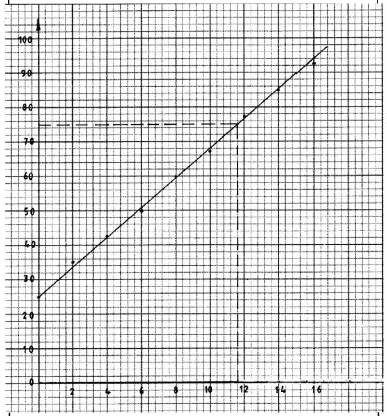
√Scale
B1 Vplotting and line of best fit- Time taken to reach = 750 C = 11.6 min
-
-
- A:B = 3:4
B:C = 1:2 B:C = 4:8
A:B:C = 3:4:8
- 3/15 x 20
= 4 litres
-
- Cost of production per litre
= 80 x 3 + 84 x 4+90 x 8
15
= Ksh 86.4
- Selling price of 1 litre for a 25% profit:
= 86.4 x125
100
= Ksh 108
- In 1h machines P and Q blend
14000 + 12000
7 5
= 2000 + 2400 - 4400 litres
Time taken to blend 550000 litres
550000
4400
= 125 hours
-
-
- Full squares = 37
Part squares = 27
Total area = 37+27
2
= 50.5 cm2
- area in km2
= 50.5 x 50000 x 50000
1000 x 1000 x 100 x 100
= 12.625 km2
M1 conversion
-
- Number of 5 ha parcels:
= 12.625 x 1000 x 1000
5 x 100 x 100
= 252.5
Number of equal parcels = 252
- Remainder in hectares:
= 0.5 x 5
= 2.5 ha
-
- Size of angle CTD = 33°
- Angle in alternate segment
- (x + 4.1) 4.1 = 72
4.1x + 4.12 = 49
4.1 x = 32.19
x = 7.851219512
≈ 7.9
-
- sin θ =sin 33
7 4.1
sinθ = 7 sin 33
4.1
= 0.9299
θ = 68°
obtuse angle = 180° - 68° = 112°
- ACT = 180° - 112° = 68°
ATC = 180° - (68 +33) = 79°
ABC - 180° - 79° - 101°
-
-
| x |
-4 |
-3.5 |
-3 |
-2.5 |
-2 |
-1.5 |
-1 |
-0.5 |
0 |
0.5 |
1 |
1.5 |
2 |
| y |
-11 |
|
|
8.1 |
|
8.4 |
7 |
|
5 |
|
9 |
|
25 |
B2 Allow B1 for 4
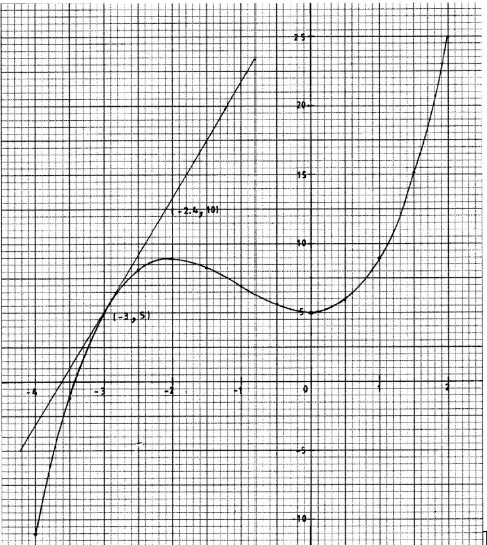
-
- 20.5 - 5.9
1.8 - 0.5
= 11.23
- tangent line at x = -3
gradient : 10 - 5
-24 - -3
= 8.3
-
-
- (x - 1)(x - 8) = 4.56
x2 - 9x + 8 = 4.56
x2 - 9x + 3.44 = 0
- x2 – 9 x +( 9 )2=( 9 )2 - 3.44
2 2 2
(x2 – 9 )2 = 81 = 3.44
2 4
(x2 – 9 ) = √16.81
2
x = 4.5 ± 4.1
= 8.6 or 0.4
x = 8.6 m
Length of pavement = 8.6 - l = 7.6 m
Width of pavement = 8.6 - 8 = 0.6 m
- No. of 0.4 m x 0.3 tiles
7.6 x 0.6
0.4 x 0.3
= 38
-
-
- Ksh. 4 000 000 x (1.2)3
= Ksh 6912 000
- 4 000 000 x (1.2)3 x (1.15)2
= Ksh 9 141 120
-
- 7125 000 x 100
95
= Ksh 7 500 000
- 9141120 × (1 - r )2 = 7500000
100
(1- r )2 = 7500000 = 0.82
100 9141120
1- r = 0.91
100
r = 1 - 0.91 = 0.09
100
r = 9%
-
-
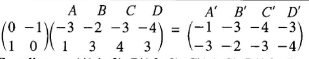
Coordinates: A'(-1,-3), B'(-3,-2), C(-4,-3), D'(-3,-4)
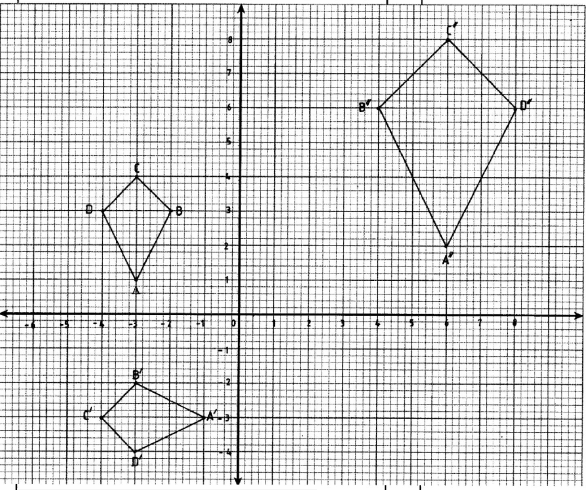
Object ABCD drawn
Image A'B'C'D' drawn
-
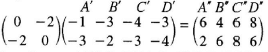
Coordinates: A"(6,2), B"(4,6), C"(6,8), D'(8,6)- image A"B"C"D" √drawn
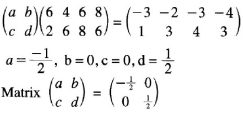
-
| Masses (kg) |
f |
Mid-point |
fx |
d=x-38 |
fd |
fd2 |
| 26 - 30 |
9 |
28 |
252 |
-10 |
-90 |
900 |
| 31 - 35 |
13 |
33 |
429 |
-5 |
-65 |
325 |
| 36 -40 |
20 |
38 |
760 |
0 |
0 |
0 |
| 41 - 45 |
15 |
43 |
645 |
5 |
75 |
375 |
| 46 - 50 |
6 |
48 |
288 |
10 |
60 |
600 |
| 51 - 5 |
2 |
53 |
106 |
15 |
30 |
450 |
| |
∑=65 |
|
∑fx=2480 |
|
∑fd=10 |
∑fd2 =2650 |
Mid points column
fx column
Mean = ∑fx = 2480
∑f 65
= 38.15
-
- variance:
∑fd 2 -(∑fd)2
∑d ∑f
= 2650 - (10)2
65 65
= 40.769 -0.02367
= 40.75
- Standard deviation
= √40.75 = 6.38

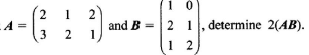 (3 marks)
(3 marks)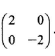



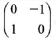 (2 marks)
(2 marks)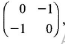 followed by an enlargement scale factor 2, centre (0,0).
followed by an enlargement scale factor 2, centre (0,0).