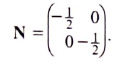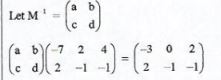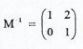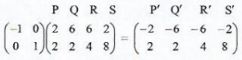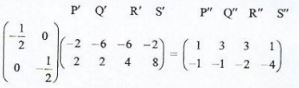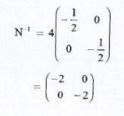KCSE 2019 Mathematics Paper 2 Questions With Marking Scheme

SECTION I (50 marks)

Answer all the questions in the spaces provided

1. Simplify .Give the answer in the form a + b√c where a, b and c are integers. (2 marks)
2. Two types of flour, X and Y, cost Ksh 60 and Ksh 72 per kilogram respectively. The two types are mixed such that the cost of a kilogram of the mixture is Ksh 70. Calculate the ratio X: Y of the mixture.(3 marks)
3. A quantity P varies inversely as the square of another quantity L. When P = 0.625, L = 4.
   Determine P when L = 0.2. (3 marks)
4. An arc of a circle subtends an angle of 150^o at the circumference of the circle. Calculate the angle subtended by the same arc at the centre of the circle. (2 marks)
5. Solve the equations:
   x + 3y = 13
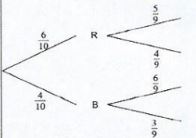
   x² + 3y² = 43   (4 marks)
6. A bag contains 6 red counters and 4 blue counters. Two counters are picked from the bag at random, without replacement.
   1. Represent the events using a tree diagram.(1 mark)
   2. Find the probability that the two counters picked are of the same colour. (2 marks)
7. Find the coordinates of the turning point of the curve y = x² - 14x + 10. (3 marks)
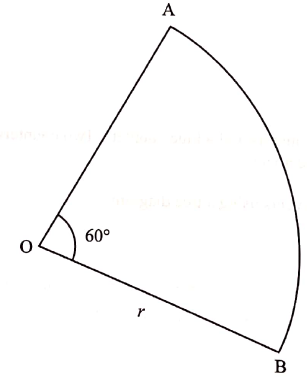
8. OAB is a sector of a circle of radius r сm. Angle AOB = 60°. Find, in its simplest form, an expression in terms of r and π for the perimeter of the sector. (2 marks)
   
9. In a mathematics test, the scores obtained by 30 students were recorded as shown in the table below.
   

   Score (x)	59	61	65	K	71	72	73	75
   No. of students	2	3	5	6	7	4	2	1

   The score K with a frequency of 6 is not given. Given that
   where d= x − 69, and using an assumed mean of 69, determine score K. (4 marks)
10. Determine the amplitude and the period of the function y = 3 sin(2x + 40°). (2 marks)
11. The figure ABCDEFGH represents a box.
    
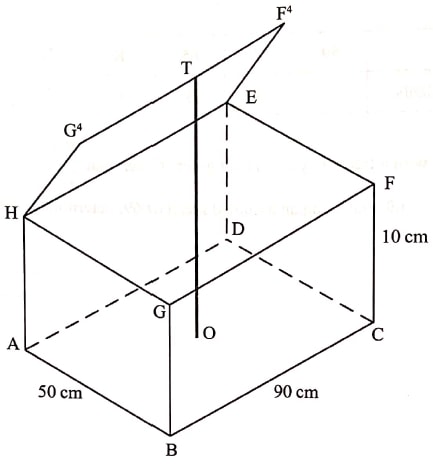
    The top lid of the box is opened such that the height OT is 35 cm. Calculate the:
    1. angle the top lid makes with the plane FGHE; (2 marks)
    2. length BE, correct to 2 decimal places. (2 marks)
12. The table below shows income tax rates in a certain year.
    

    Monthly income in Ksh.	Tax rate in each shilling (%)
    0 - 10164	10
    10165 - 19740	15
    19741 - 29316	20
    29317 - 38892	25
    38893 and above	30

    In that year, Mawira camed a salary of Ksh 41 000 per month. Calculate Mawira's income tax per month given that a monthly tax relief of Ksh 1162 was allowed. (3 marks)
13. The position vectors of points A, B and Care OA = , 0B =  and OC = .
    Show that A, B and C are collinear. (3 marks)
14. The vertices of a triangle PQR are P(-3,2), Q(0, −1) and R(2, −1). A transformation matrix M maps triangle POR onto triangle P'O'R' whose vertices are P'(−7,2), Q' (2, 1) and R (4, −1). Find M⁻¹, the transformation that maps P'Q'R' onto PQR. (4 marks)
15. Solve for x in log(7x − 3)+2 log 5 = 2 + log(x + 3). (4 marks)
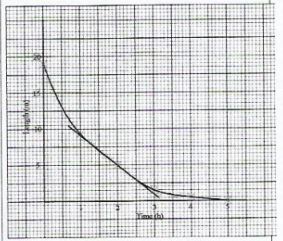
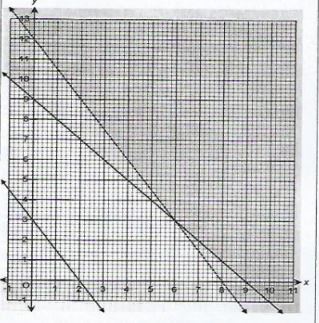
16. The length of a shadow of a mast was measured at intervals of 1 hour and recorded as shown in the table below.
    

    Time(h)	0	1	2	3	4	5
    Length (m)	18.7	8.7	5.0	2.9	1.3	0

    1. On the grid provided, draw the graph of length against time. (2 marks)
       
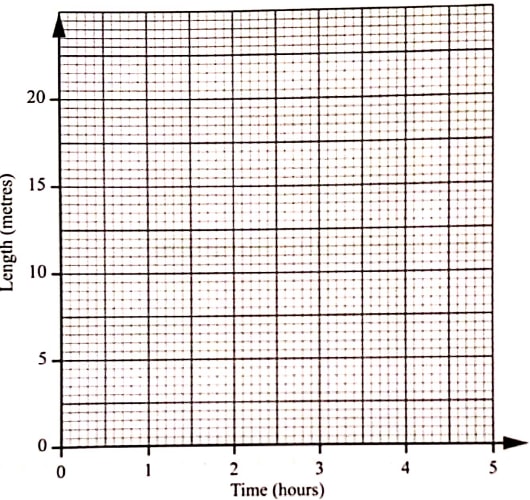
    2. Determine the rate of change of the shadow length at I = 2. (2 marks)

SECTION II (50 marks)

Answer any five questions in this section

1. The first term of an Arithmetic Progression (AP) is equal to the first term of a Geometric progression (GP). The second term of the AP is equal to the fourth term of the GP while the tenth term of the AP is equal to the seventh term of the GP.
   1. Given that a is the first term and d is the common difference of the AP while r is the common ratio of the GP, write the two equations connecting the AP and the GP. (2 marks)
   2. Find the value of r that satisfies the progressions. (4 marks)
   3. Given that the tenth term of the GP is 5120, find the values of a and d. (2 marks)
   4. Calculate the sum of the first 20 terms of the AP. (2 marks)
2. Mbaka bought some plots at Ksh 400 000 each. The value of each plot appreciated at the rate of 10% per annum.
   1. Calculate the value of a plot after 2 years. (2 marks)
   2. After some time t, the value of a plot was Ksh 558 400. Find 1, to the nearest month. (4 marks)
   3. Mbaka sold all the plots he had bought after 4 years for Ksh 2928200. Find the percentage profit Mbaka made, correct to 2 decimal places. (4 marks)
3. The figure KLMN below is a scale drawing of a rectangular piece of land of length KL = 80 m
   
   
   1. On the figure, construct:
      1. the locus of a point P which is both equidistant from points L and M and from lines KL and LM. (3 marks)
      2. the locus of a point such that 2 KQL. = 90° (3 marks)
   2.  
      1. Shade the region R bounded by the locus of Q and the Locus of points equidistant from KL and LM. (1 mark)
      2. Find the area of the region R in mo. (Take π = 3.142) (3 marks)
4. A ship left point P(10°S, 40°E) and sailed due East for 90 hours at an average speed of 24 to a point R. (Take 1 nautical mile (nm) to be 1.853 km and radius of the earth to be 6370 km)
   1. Calculate the distance between P and R in:
      1. nm; (1 mark)
      2. km. (1 mark)
   2. Determine the position of point R. (5 marks)
   3. Find the local time, to the nearest minute, at point R when the time at P is 11:00 a.m. (3 marks)
5. A workshop makes cupboards and table two artisans A and B. Every cupboard made requires 3 days of work by artisan A and 2 days of work by artisan B. Every table made requires 2 days of work by artisan A and 2 days of work by artisan B. In one month artisan A worked for less than 24 days while artisan B worked for not more than 18 days. The workshop ma cupboards and y tables in that month. The workshop made x cupboards and y tables in that month.
   1. Write all the inequalities which must be satisfied by x and y. (3 marks)
   2. Represent the inequalities in (a) on the grid provided. (3 marks)
      
   3. The workshop makes a profit of Ksh 6 000 on each cupboard and Ksh 4000 on each table. Find the number of cupboards and the number of tables that must be made for maximum profit and hence determine the maximum profit. 
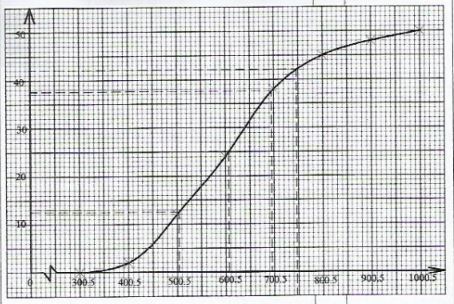
6. The amount of money contributed by a group of students during a fundraising for a needy student was as shown in the table below.
   

   Amount(Ksh)	301 - 400	401 - 500	501 - 600	601 - 700	701 - 800	801 - 900	901 - 1000
   Number of students	2	10	12	14	7	3	2

   1. On the grid provided, draw an ogive to represent the data. (4 marks)
      
   2. Use the graph to estimate: 
      1. the median; (1 mark)
      2. the quartile deviation; (3 marks)
      3. the percentage number of students who contributed at least Ksh 750.50. (2 marks)
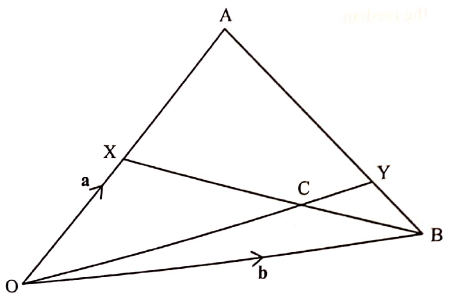
7. In the figure below, OA = a, OB = b and BX meets OY at C. OX:OA = 1:2 and BY:YA = 1:3
   
   
   1. Express in terms of a and b:
      1. BA; (1 mark)
      2. OY; (2 marks)
      3. BX. (1 mark)
   2. Given that OC = hOY and BC = kBX, determine the values of h and k. (6 marks)
8. A trapezium PQRS with vertices P(2, 2), Q(6,2). R(6, 4) and S(2, 8) is mapped onto P'Q'R'S DY a transformation matrix (2 marks)
   1. Find the coordinates of P'Q'R'S'. (2 marks)
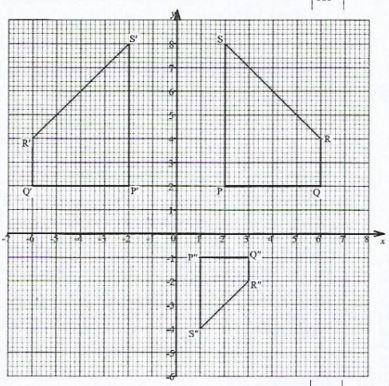
   2. On the grid provided draw PQRS and its image P'Q'R'S'.
      
   3.  
      1. Find P"Q"R"S". the image of P'O'R'S' under the transformation matrix, (1 mark)
         
      2. On the same grid draw P'Q"R"S". (1 mark)
   4.  
      1. Find a single matrix that maps P"Q"R"S" onto P'Q'R'S'. (2 marks)
      2. Describe fully the transformation that maps P'Q"R"S" onto P'Q'R'S'. (2 marks)

Marking Scheme

1. √15 + 3 = (√15 + 3)  x (√15 + 2)
   √15 - 2      (√15 - 2)     (√15 + 2)
   = 5+2√5+3√5 +6
               5-4
   = 11 + 5√5
   
   
2. Let the ratio of X to Y = x:y              Let the ratio of X to Y = 1:n
   60x + 72y = 70                                  60 + 72n = 70
      x+ y                                                   1+n
   60x + 72 y = 70x + 70y                   60 + 72n = 70 + 70n 
   10x = 2y                                           2n = 10
    x  =  2  or  1                                              n = 5
    y     10      5
   Ratio x: y = 1:5                                   Ratio x: y = 1:5
   
   
3. Pα¹/_L²
   0.625 =^K/₁₆
   K = 10
   When L = 0.2
   P = ¹⁰/_0.2²
   = 250
   
   
4. Angle at centre = 2x150° = 300°
5.   x = 13 - 3y
   (13–3y)² + 3y² = 43
   169 - 78y + 12y²= 43
   12y² - 78y + 126 = 0
   2y² - 13y + 21 = 0
   (2y-7)(y-3) = 0
   y = 3 or 3.5
   When y = 3, x = 4
   When y = 3.5, x = 2.5
6.      
   1.     
      
   2.  P(RR or BB) = ⁶/₁₀ x ⁵/₉ + ⁴/₁₀ x ³/₉
      ¹/₃ + ²/₁₅
      =⁷/₁₅
7. ^dy/_dx = 2x - 14 = 0
   at the turning point
   ^dy/_dx= 2x -14=0
   x = 7
   y = 49 - 98 + 10 = -39
   Coordinate of turning point = (7,-39)
   
   
8. Perimeter of sector = 60/360 x 2πr + 2r
   = 2r + ¹/₃πr
9.       
   Σfd = 6k - 438 =-1.2
    Σf           30
   6k = 402
   k = 67
   
   
10. Amplitude = 3
    Period = ³⁶⁰/₂ = 180º
11.      
    1. Sin θ = 25/50
       θ = Sin^-1(½)
       = 30°
       
       
    2. BE = √(90² +50² +10²)
       = √10700
       = 103.44
12. Tax before relief
    {10164 x 0.1 + 9576 x (0.15 +0.2 +0.25) +2108 x 0.3}
    = 7394.4
    Net tax = Ksh (7394.4 - 1162)
    = Ksh 6232.4
13.      
    
    k=0.4
    AB // AC and A is a common point.
    ∴Points A, B and C are collinear.
    
    
14.    
    
    
    -7a + 2h = -3              -7c + 2d = 2
    2a-b=0 or b= 2a          2c-d=-1 or d = 2c + 1
    -7a + 2x2a = -31        -7c + 2(2c + 1) = 2
      -3a = -3                    -3c = 0
    a = 1, b = 2                 C = 0, d = 1
    
    Therefore
    
15. 2 = log 100
    log (7x - 3) + log 5² = log 100 + log(x+3)
    log (25(7x - 3)) = log (100(x+3)}
    25(7x - 3) = 100(x+3)
    7x-3=4x+12
    3x=15
    x=5
16.      
    1.           
       
    2. Acceptable tangent drawn at t=2
       Tangent passes through points
       (2,5) and (2.5,3.5)
       ΔL = 3.5-5 = -1.5
       Δt     2.5-2     0.5
       =-3.0 m/s
17.          
    1. ar³= a +d
       ar⁶ = a + 9d
       
       
    2. From (a) above
       d = ar³ - a
       a +9(ar³ -a) = ar⁶
       a +9ar³ - 9a = ar⁶
       ar⁶ - 9ar³ +8a =
       r⁶ - 9r³ +8 = 0
       (r³-1)(r³-8) = 0
       r = 1 or r = 2
       r = 2
       
       
    3. ar³ = 5120
       a = 5120  = 10
                2⁹
       a+d = 10x2³ = 80
       ∴d = 80-10 = 70
       
       
    4. S₂₀= ²⁰/₂{20+19x70)
       = 13500
18.            
    1. Value of a plot after 2 years
       = 400 000x1.1²
       = Ksh. 484 000
       
       
    2. 558 400 = 400 000(1.1)^t
       1.1^t =   558 400   
                   400 000
       1.1^t = 1.396
       t log 1.1 = log 1.396
       t = log 1.396 = 3.500
                log1.1
       = 3 years 6 months (or 42 months)
       
       
    3. Let the number of plots bought be x
       x x 400 000 X (1.1)⁴ = 2928 200
       x =       2 928 200               =   2928 200   
                400 000 X (1.1)⁴              585 640
       =5
       Profit = 2928 200 - 5 x 400 000
       = 928 200
       % profit =     928 200      x100%
                         2 000 000
       = 46.41%
19.       
    1.       
       1. bisector to line LM
          Bisector to <KLM
          Position of P correctly identified
       2.  bisector to line KL
          Correct centre used
          Locus of Q correctly drawn
    2.           
       1. Correct region R shaded and labelled
       2. I=40 m
          Area of region R
          =    90   x 3.142 x 40² - ¹/₂ x 40 x 40
                360
          = 1256,8-800
          = 456.8m²
20.            
    1.           
       1. Distance in nm
          = 24x90
          = 2160 nm
          
          
       2. Distance Km
          = 2160x1.853
          = 4002.48 km
          
          
    2. Position of R
       1° = 60 cos 10nm
       θ = <PO₁R
       θ =    2160   
             60cos 10
       = 36.56°
       Position of R = (10°S, (40 + 36.56)°E)
       = (10°S, 76.56°E)
       
       
    3. Local time at R
       Longitude difference between P and R= 36.56°
       Time difference = 36.56 x 4
                                        60
       =2hrs 26mins
       Local time at R
       = 1100h + 2h 26min
       = 1326h
       = 1.26 pm
21.            
    1. x>0, y > 0
       2x + 2y < 18 or x + y < 9
       3x + 2y < 24
       
       
    2.    
       
    3. Objective function
       6000x + 4000y=P
       6000x + 4000 y = 12000 or 3x + 2y = 6
       Or two feasible points inspected
       x=5, y=4 and x = 7, y=1
       Profit =sh (6000x5 + 4000 x 4) or (6000x7 + 4000 x1) = sh 31600
22.          
        
    1. c.f. 2, 12, 24,38,45,48,50
    2.      
       1. Median = Contribution of 25th student = 605.5
       2. Quartile deviation
          Q3= Contribution of 37.5 student = 695.5
          Q1 = Contribution of 12.5 student = 505.5
          Q₃ - Q₁ = 695.5 - 505.5
              2                    2
          = 95
       3. No of people who contributed at least Ksh 750.5
          =9
          % = ⁹/₅₀ x100
          = 18%
23.          
    1.        
       1. BA=a - b
          Accept ratio thm
       2. OY = b + ¹/₄ (a - b)
          ³/₄b + ¹/₄a
       3. BX = -b + ¹/₂a
          
          
    2. OC = h(¼a + ¾b)
       OC= b+k(½a - b)
       h(¼a + ¾b)= b+k(½a - b)
       ¼ha + ¾hb= ½ka +(1-k) b
       ¼h=½k →h=2k
       ¾h=1-k
       ¾(2k)=1-k
       10k=4
       k=²/₅
       h=⁴/₅
24.          
    1.      
         
       Coordinates:
       P'(-2,2), Q'(-6,2), (R'(-6,4), S'(-2,8)
       
       
    2. Trapezium PQRS correctly drawn
       Trapezium P'Q'R'S' correctly drawn
    3.      
       1.          
          
       2. Trapezium P"Q"R"S" correctly drawn
    4.          
       1. The matrix is N'
          Det = ½ x ½ - 0 x 0 = ¼
          
       2. Enlargement centre 0(0,0)
          S.F= -2