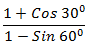SECTION 1 (50 MARKS)
Answer all questions in this section in the spaces provided.
- A positive two digit number is such that the product of the digits is 24. When the digits are reversed, the number formed is greater than the original number by 18. Find the number. (2mks)
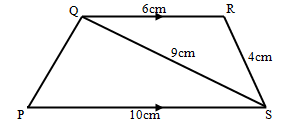
- In the figure below PQRS is a trapezium with QR parallel to PS. QR = 6cm, RS = 4cm, QS = 9cm and PS = 10cm.
Calculate to two decimal places- The size of angle SQR (2Marks)
- The area of triangle PQS (2Marks)
- The height and radius of a cone are measured as 21 cm and 14.0 cm respectively. Taking π= 3.142, find the percentage error in the volume of the cone. (4mks)
- Express the following in surd form and simplify by rationalizing the denominator without using a calculator and leave your answer in the form a + (3mks)
- Solve for x in:
Log2(x + 7) – Log2(x – 7) = 3(3mks - A businessman obtained a loan of Ksh 450,000 from a bank to buy a Matatu that was valued at the same amount. The bank charges interest at 24% per annum compounded quarterly per year. Calculate the total amount of money the businessman paid to clear the loan in 6 1/2 years to the nearest shilling. (2mks)
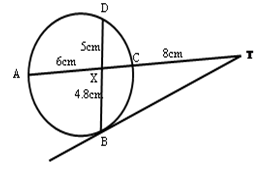
- In the diagram below, BT is a tangent to the circle at B. AXCT and BXD are straight lines. AX = 6cm, CT = 8cm, BX = 4.8cm and XD = 5cm.
Find the length of BT. (3Marks)
- Find the possible values of x given that
is a singular matrix. (3mks)
- The cost C of operating an electronic business is partly constant and partly varies as the square of labour input L. If C=25,000 when L=20 and C=45,000 when L=30. Find C when L=8. (3Mks)
- The 2nd, 4thand 7th terms of an A.P. are the first 3 consecutive terms of a G.P. Find the common ratio of the G.P if the common difference of the A.P. is 2. (3mks)
- P and Q are two points such that OP=i + 2j + 3k and OQ = 4i + 5j – 3k. M is a point that divides PQ externally in the ratio 3:2. Find the co-ordinates of M, given that O is the origin. (2mks)
- Two bags labeled A and B are on the table. Bag A contains 5 red balls and 3 white balls, while bag B contains 2 red balls and 6 white balls. A bag is chosen at random and two balls are drawn from it, one after the other without replacement. Find the probability that the two balls chosen are of different colours. (4mks)
- Tap A can fill an empty tank in 3 hours, while tap B can fill the same tank in 2 hours. When the tank is full, tap C can empty the tank in 5 hours. Tap A and C are opened for 4 hours and then closed.
- Determine the fraction of the tank that is still empty.(2mks)
- Find how long it would take to fill the remaining fraction of the tank if all the three taps are opened.(2mks)
- Determine the interquartile range for the following set of numbers.(3mks)
4, 9, 5, 4, 7, 6, 2, 1, 6, 7, 8. - Solve the equation Sin(3x – 10)0= 0.4337 for 00≤Ɵ≤1800(3mks)
- Expand and simplify (3x – y)4(2mks)
- Use the first three term of the expansion to approximate the value of (6 –0.2)4 (2mks)
SECTION 1I (50 MARKS)
Answer any five questions from this Section.
- Taking the radius of the earth, R= 6370km and π = 22/7, calculate the shortest distance between the two cities P (24oN, 29o48’W) and Q(24oN, 30o12’E) along the parallel of latitude.
- In nautical miles. (3mks)
- In Km. (2mks)
- If it is 1200hrs at P, what is the local time atQ. (2mks)
- An airplane flew due south from a point A (60oN, 45oE) to a point B. The distance covered by the airplane was 8000km. Determine the position of B. (3mks)
- Taking the radius of the earth, R= 6370km and π = 22/7, calculate the shortest distance between the two cities P (24oN, 29o48’W) and Q(24oN, 30o12’E) along the parallel of latitude.
- A particle moves along a straight line such that its displacement S metres from a given point is S= t3-5t2 + 3t + 4.
- The displacement of the particle at t=5 (2mks)
- The velocity of the particle when t=5 (3mks)
- The value of t when the particle is momentarily at rest. (3mks)
- The acceleration of the particle when t=2. (2mks)
- A solution was gently heated, its temperature readings taken at intervals of 1 minute and recorded as shown in the table below.
The points with coordinates (5,5) and (-3, -1) are the ends of a diameter of a circle center A. Determinea) Draw the time-temperature graph on the grid provided (3mks)Time (min)
0
1
2
3
4
5
Temperature(0C)
4
5.2
8.4
14.3
16.8
17.5

- Use the graph to find the average rate of change in temperature between t = 1.8 and t = 3.4 (2mks)
- The coordinates of A. (2mks)
- The equation of the circle, expressing it in form of x2 + y2 + ax + by + c = 0 (3mks)
- A solution was gently heated, its temperature readings taken at intervals of 1 minute and recorded as shown in the table below.
- Mrs.Mutua earns a basic salary of K£ 12,000 p.a. and is housed by the employer at a nominal rent of Shs 1,200 per month. She is entitled to a personal relief of K£ 1,320 p.a. and a premium relief of 10% on her insurance premium of K£ 800 p.a. The housing benefit when you are housed by the employer is 15% of the basic salary. The table of tax rate is as below.
Calculate the net tax per annum. (7mks)Calculate;Taxable income (K£ p.a.)
Rate (%)
1 – 2100
10
2101 – 4200
15
4201 – 6300
20
6301 – 8400
25
Over 8400
30
- Other deductions includes W.C.P.S Shs 600 per month, NHIF Shs. 500 per month. Calculate her net pay per month. (3mks)
- Using a ruler and a compass only, construct a triangle ABC such that AB = 6.8 cm, BC = 5.6 cm and angle ABC = 37 ½ o (3mks)
- Locate the :
- Locus P such that angle APB = angle ACB (3mks)
- Locus Q such that Q is equidistant to points A and B (2mks)
- Locus R such that R is equidistant to lines AB and AC (2mks)
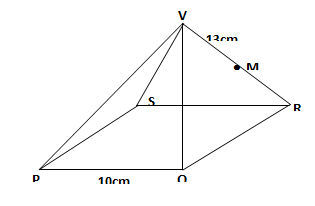
- The diagram below shows a square based pyramid V vertically above the middle of the base. PQ = 10cm and VR = 13cm. M is the midpoint of VR.
Find to 2 decimal places- the length PR. (2mks)
- The height of the pyramid. (2mks)
- the angle between VR and the base PQRS. (2mks)
- The angle between MR and the base PQRS. (2mks)
- The angle between the planes QVR and PQRS.(2mks)
- A farmer has at least 50 acres of land on which he plans to plant potatoes and cabbages. Each acre of potatoes requires 6 men and each acre of cabbages require 2 men. The farmer has 240 men available and he must plant at least 10 acres of potatoes. The profit in potatoes is Ksh 1,000 per acre and on cabbages ksh. 1,200 per acre. If he plants x acres of potatoes and y acres of cabbages:
- Write down three inequalities in x and y to describe this information.(3mks)
- Represent the above inequalities on the graph below.(5mks)

- Use your graph to find the number of acres of each crop that the farmer should plough to get maximum profit. Calculate the maximum profit.(2mks)
- On the grid provided, draw a graph of the function y= x2 – x + 3 for 0≤ x ≤ 6.(3mks)

- Determine the midordinates for 5 strips between x=1 and x=6, and hence use the mid-ordinate rule to approximate the area under the curve between x=1 and x=6 and and the x-axis.(3mks
- Assuming that the area determined by integration to be the actual area, calculate the percentage error in using the mid-ordinate rule.(4mks)
- On the grid provided, draw a graph of the function y= x2 – x + 3 for 0≤ x ≤ 6.(3mks)

MARKING SCHEME







Download MATHEMATICS PAPER 2 - 2019 LAINAKU JOINT MOCK EVALUATION EXAMINATION.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students