QUESTIONS
SECTION I: (50MKS)
ATTEMPT ALL THE QUESTIONS FROM THIS SECTION
- Without using a calculator or a mathematical table evaluate (3mks)
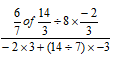
- In a disco hall, four lights signals are programmed at intervals of 8 seconds, 10 seconds, 12 seconds and 15 seconds. What is the earliest time they will give out light signals simultaneously if the last time they did this 1915 Hrs. (3mks)
- Simplify (3mks)
12x2 - 16x
20 - 11x - 3x2 - The number of sides of two regular polygons differ by one. If the sum of the interior angles of these polygons is in the ratio 3:2 calculate the number of sides of each polygon and name them. (4mks)
- Under an enlargement scale factor -4 the image of point A(4,3) is A1(-4,-5). Calculate the coordinates of the centre of enlargement. (3mks)
- Given that A+(20 03) = (20 31) find AT the transpose of matrix A. (2 mks)
- If
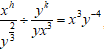 , find h +k (3mks)
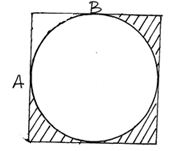
, find h +k (3mks) - The figure below shows a circle inscribed in a square. The length of the arc AB is 44/7√7cm. Calculate the area of the shaded region. π = 22/7 (4mks)
- Two students Paul and Omondi standing 10m apart on the same side of a tall building on a horizontal ground. Paul who is closer to the building sees the roof top at an angle of 70º, while Omondi at an angle of 46.8º, if the building, Paul and Omondi lies on a straight line, calculate the height of the building correct to 3 s.f. (4 mks)
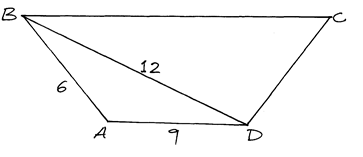
- A trapezium was created by joining two similar triangles. What is the perimeter of the quadrilateral? (3mks)
- Mr Wajakoya purchased animal feeds for his 10 cows which would last for 7 days. After feeding his cows for 4 days, he sold 4 cows. How many more days will the feeds last the remaining cows. (3mks)
- Use the tables of logarithms to evaluate. (4mks)
(6.79 x 0.391)-3/4
log5 - A pentagonal prism has each of its sides as 5cm and length 10cm. Find the volume of the prism.(3 mks)
- Solve the following inequalities and state the integral solutions. (3mks)
½(24 - 4x) > 6(3x - 4/3) ≥ -2/3(42 + 3x) - When a shirt is sold at sh 126 a loss of x% is made. If the same shirt is sold at sh 154, a profit of x% is realized. Find the buying price of the shirt. (3mks)
- Without using calculator or mathematical tables, find the value of x in sin60º = cos (3x-45)º given that 0º ≤ x ≤ πc/2 (2mks)
SECTION II : ANSWER ANY FIVE QUESTIONS
- The figure below shows a line that passes through points P, Q and R. Given that its equation is -7y/30 + x/10 = 1 and that point Q is equidistant from x and y-axis
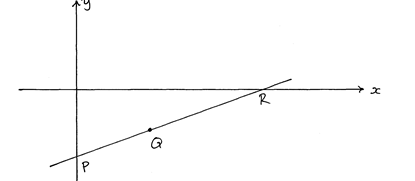
- Calculate the co-ordinates of points Q. (4mks)
- Calculate the size of angle formed by the line and y-axis. (3mks)
- Find the equation of the perpendicular to the line through Q in the form of x/a + y/b = 1 (3 mks)
- The figure below shows a histogram of a certain data.
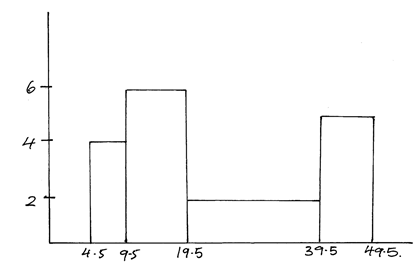
- Given that the frequency of the last class is 30, prepare frequency distribution table for the data. (3mks)
-
- State the modal class. (1 mk)
- Estimate the mean height (3mks)
- Using a vertical line show where the median lies and state the median. (3mks)
- Towns A and B are 420km apart. Two Lorries departed from A at the same time travelling towards B. Lorry X travelled at an average speed of 15km/h less than Y and reached 1 hour and 24 minutes later.
- Calculate the average speed of lorry Y. (5mks)
- How far was X from A when Y reached B. (2mks)
- A van left town B heading towards A at the time lorries X and Y left A. If the van travelled at an average speed of 90km/h, how far from A did it meet Lorry Y. (3mks)
- The vertices of a triangle PQR are P(0,0), Q(6,0) and R(2,4).
- Draw triangle PQR on the grid provided. (1mk)
- Triangle P1Q1R1 is the image of triangle PQR under an enlargement scale factor and centre (2,2), write down the co-ordinates of P1Q1R1 and plot on the same grid. (3mks)
- Draw triangle P11Q11R11 the image of triangle P1Q1R1 under a positive quarter turn about point (1,1). State the co-ordinates of P11Q11R11. (3mks)
- Draw triangle P111Q111R111 the image of P11Q11R11 under a reflection in the line y=1. (2mks)
- State the type of congruence between triangle P1Q1R1 and P111Q111R111. (1mk)
- The diagram below represents a solid consisting of a hemispherical bottom and a conical frustum at the top. O1O2 =4cm, O2B=R=4.9cm and O1A=r=2.1cm.
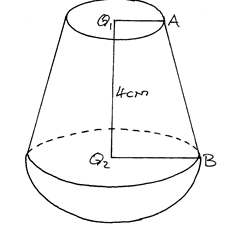
Calculate to 1 d.p,- The height of the chopped off cone and hence the height of the bigger cone. (2mks)
- The surface area of the solid. (4mks)
- Calculate the volume of the solid. (4mks)
- In the triangle below P and Q are points on OA and OB respectively such that OP:PA=3:2 and OQ:QB =1:2 AQ and PQ intersect at T. Given that OA= a and OB= b
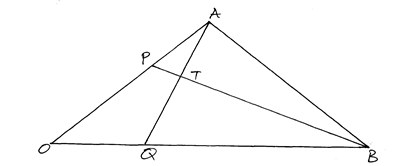
- Express AQ and PQ in terms of a and b (2mks)
- Taking BT=kBP and AT=hAQ where h and k are real numbers.
- Find two expressions for OT in terms of a and b (2mks)
- Use the expressions in b(i) above to find the values of h and k. (3mks)
- Show that B, T and P are collinear. (3mks)
- A ship leaves port M and sails on a bearing of 0500 heading towards island L. Two navy destroyers ships sail from a naval base N to intercept the ship. Destroyer A sails such that it covers the shortest distance possible. Destroyer B sails on a bearing of 010º to L. The bearing of N from M is 100º and distance NM=300km. Using a scale of 1cm represents 50km, determine;
- The position of M, N and L. (5 mks)
- The distance travelled by destroyer A. (2mks)
- The distance travelled by destroyer B. (2mks)
- The bearing of N from L. (1mks)
-
- Determine the x and y-intercepts of the curve y=(x-1) (x+3)2 (3mks)
- Find the stationary points of the curve above and state their nature. (4mks)
- Sketch the curve. (3mks)

MARKING SCHEME
- Num
6/7 x 14/3 = 4 ÷ 8 x -2/3
= ½ x -2/3 = -1/3
Den
-6 + 2 x -3
-6 + -6
= -12
-1/3 ÷ -12 = -1/3 x -1/12 = 1/36 - L.C.M = 23 × 3 × 5 =120
120/60 = 2mins
Next time = 1915
+ 2
1917 Hrs - 4x(3x - 4)
(5+x)(4-3x)
= -4x
x+5 - Let the polygons have n& n-1 sides
(n-2) 180: (n-1-2)180=3:2
180n - 360 = 3/2
180n - 540
900 -180n
n=5
Therefore n=5 → pentagon
-1=4 → Quadrilateral - -4[43 -x-y] = [-4-5 -x-y]
-16 +4x=-4-x
-12+4y = -5 - y
x=2.4 y=1.4
centre (2.4, 1.4) -
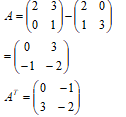
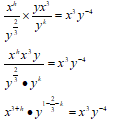
3 + h = 3
h = 0
= 1/3 - k = -4
k = 41/3
h + k = 0 + 41/3 = 41/3- 44/7√7 = 90/360 x 22/7 x r
r = 44/7√7 x 4/1 x 7/22 = 8√7
Area of square – Area of Circle
(16√7 x 16√7) - 22/7 x (8√7)2
= 1792 - 1408 = 384
Area of the shaded part
= ¾ x 384
= 288cm2 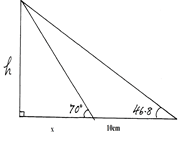
Tan70 = h/x ; h = xtan70
tan46.8 = h ; h = (x + 10)tan46.8
x + 10
xtan70 = (x + 10)tan46.8
2.7475x = 1.06589x + 10.6589
1.6826x = 10.6589
x = 6.3347
h = 6.3347tan70
= 17.4m- BC/12 = DC/6 = 12/9
DC =12 x 6 = 8
9
BC = 12 x 12 = 16
9
Perimeter = 16 + 8 + 9 + 6 = 39cm - 1 COW -70 DAYS
1cow takes 1/70 of feeds
1/70 x 10 = 1/7
1/7 x 4 = 4/7
Remaining cows 10 - 4 = 6 ⇒ 1/70 x 6 = 3/35 of feeds per day
1 day - 3/35
? - 3/7
1 x 3/7 x 35/3 = 5days - ( Log5 )¾
6.79 x 0.391
No Log 0.6990
6.79
0.391
3.675 x 10-1
0.36751.8445
0.8319
1.5922
0.4241
1.4241 x ¾ = 2.2612
4
4 + 2.2612
4
1.5653 - C.A = 5 x ¼ x 5 x 5tan54
C.A = Vol = 5 x ¼ x 5 x 5tan54 x 10
= 430.1cm3 - 12-12x>18x-8 -28-2x
12-2x>18x-8
20>20x
1>x
18x-8 -28-2x
20x -20
x -1
-1 x<1
integral values -1, 0 - Let B.P be T
%loss = (T - 126) x 100 = x%
T
%profit = (154 - T) x 100 = x%
T
(T - 126)100 = (154 - T)100
T T
T - 126 = 154 - T
2T = 280
T = sh140 - 60+3x-45=90
3x=75
x=25º
360º - 2πc
25º= ?
x = 5πº
36 -
- y - intercept = -30/7
P(0, -30/7)
x - intercept = 10
R(10,0)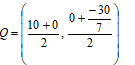
(5,-15/7) - Tanℑ = Δx/Δy
tanℑ = 10/30/7
ℑ = tan-1(70/30) = 66.80º - grade of line PQR = 3/7
Grade of ⊥r line = -7/3
y - -15/7 = -7
x - 5 3
y + 15/7 = -7/3x + 35/3
y = -7/3x + 200/21
21/200(y + 7/3 x) = 200/21 x 21/200
21y/200+ 49/200x = 1
- y - intercept = -30/7
-
-
5 = 30/10n ; n = 5/3class mid-point frequency fx 4-9
10-19
20-39
40-496.5
14.5
29.5
44.512
36
24
30
∑f = 10278
522
708
1335
∑fx = 2643
2 = f/20 x 5/3 ⇒ f = 24
f = 6 x10 x 3/5 = 36
f = 4 x 5 x 3/5 = 12
Modal class 10-9 - x = ∑fx = 2643 = 25.91
∑f 102 - Area of the bars
(4 x 5) + (10 x 6) + (20 x 2) + (10 x 5) = 170
Media = 170/2 = 85
(4 x 5) + (10 x 6) + (2 x y) = 85
2y = 85 - 80
y = 2.5
Verticallineat 19.5 + 2.5 = 22
-
-
- Time by Lorry X= 420/x hrs
Time by Lorry Y = 420/x+15
420/x - 420/x+15 = 1hr 24mins
420(x + 15)-420x = 7/5
x(x + 15)
420x + 6300 - 420x = 7/5(x2 + 15x)
7x2 +105x-31,500=0
x2+15x-4500=0
x2 +75x-60x-4500=0
x(x+75) - 60(x+75)=0
(x-60) (x+75)=0
x = 60 or x = -75 ignore - Therefore speed of lorry Y = 60+15 = 75km/h
Time by Y = 420/75 = 5.6hrs = 5hrs 36mins - Distance by X from A = 60×5.6=336km
R.S = 90+75 =165
time they took to meet = 420/165 = 2.54hrs
Distance from A = 75 × 2.54= 190.9km
- Time by Lorry X= 420/x hrs
-
-
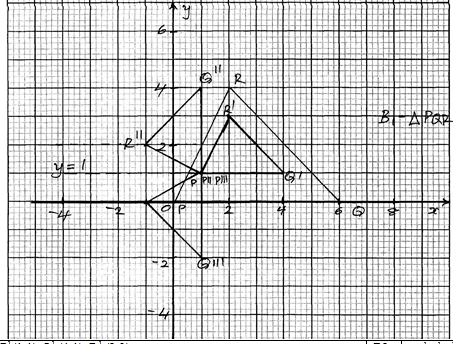
- P1(1,1) Q1 (4,1) R1 (2,3)
- P11 (1,1) Q11(1,4) R11 (-2,2)
- Indirect congruent
-
-
- L.S.F = 4.9/2.1 = 7/3
4th/h = 7/3
12 +3h = 7h
4h=12
h=3cm
H=7cm - L = √72 + 4.92 = 8.5446
l = √32 + 2.12= 3.6620
Top = 22/7 x 2.12 = 13.86cm2
C.S.A = 22/7 x 4.9 x 8.5446 - 22/7 x 2.1 x 3.6620
= 131.59 - 24.17 = 107.42cm2
TSA = 13.86 + 107.42 + 150.92 = 272.2cm2
Total Vol= 246.5+12.21 - 2/3 x 22/7 x 4.93 = 246.5cm3
1/3 x 22/7 x 4.92 x 7 - 1/3 x 22/7 x 2.13 x 3 =408.71cm3
= 176.07 - 13.86 = 162.21
Total vol = 246.5 + 12.21
= 408.71cm3
- L.S.F = 4.9/2.1 = 7/3
-
- AQ = AO + OQ
= a + 1/3b
PQ = PO + OQ
= -3/5a + 1/3b -
- OT = OA + AT
a + h (-a + 1/3b) = a - ha + 3/5hb
OT = OB + BT
= b + kBP = b + k(3/5a - b)
-b - kb + 3/5ka - 1-h = 3/5k 3/5h=1-k
5 - 5h = 3k h = 3 - 3k
5 - 5(3 - 3k) = 3k
-10 + 15k = 3k
k = 5/6; h = 3 - 3(5/6) = ½
- OT = OA + AT
- BT = kBP
BT = 5/6BP
SO BT//BP and point B common so B, T &P are collinear.
- AQ = AO + OQ
-
-
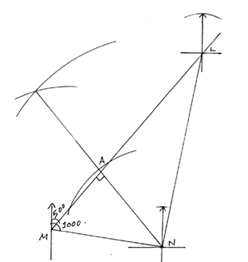
- 5.3 × 50
= 265km - 10.8×50
=540 km - 190º
-
-
- x-intercept, y=0
0=(x-1) (x+3)2
x=1,
x=-3
Y-intercept, x=0
y= (-1) (9)
=-9 - at stationary point. dy/dx = 0
(x-1) (x2 + 6x+9)
=x3 + 5x2 + 3x-9
dy/dx = 3x2+ 10x+3
3x2+10x+3=0
3x+9x+x+3=0
(3x+1) (x+3) =0
x= -1/3 or x=-3
(-1/3 , -913/27)min, (-3,0)max -
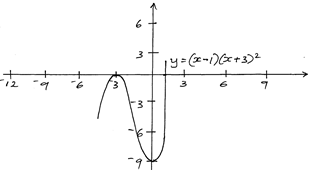
- x-intercept, y=0
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - Cekenas Mock Exams 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students
