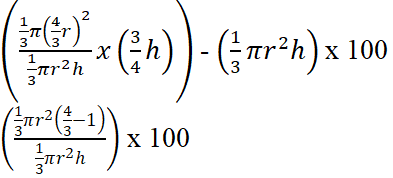Instructions to Candidates
- The paper contains TWO sections: Section I and II
- Answer ALL questions in section I and STRICTLY ANY FIVE questions from section II.
- All working and answers must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
- Marks may be awarded for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used except where stated otherwise.
SECTION I(50 Marks):
Answer ALL questions in the section in the space provided.
- Use logarithm tables correct to 4 significant figures to evaluate. (3 Marks)
∛(0.07214 x 2.037)
69.8 - Find the equation of the perpendicular bisector of line PQ where the co-ordinates of P and Q are P (-2, 8) and Q (4, 7). (3 Marks)
- The surface areas of two spheres are 36cm2 and 49cm2. If the volume of the smaller sphere is 20.2cm3, calculate the volume of the larger one. (2 Marks)
- The marked price of a shirt is Sh. 800. A customer buys the shirt after being given a discount of 13%. The seller then realizes that he made a profit of 20% on this sale. Find how much the seller had bought the shirt. (2 Marks)
- In the grid provided below, show the region R that is satisfied by the three inequalities given below.
Y≤6 – x
y<x + 4
y≥2 (4 Marks) - The radius of a cone increases in the ratio 4:3 while it’s height decreases in the ratio 3:4. Determine the percentage change in the volume of the cone. (3 Marks)
- Solve for x in the equation (3 Marks )
Log (5x + 75) – 2 Log 3 = Log (2x – 9) - Given that a = 3i – 2j + 3k and b = 2i - 4j – 3k where i, j and k are unit vectors, find |2a + 3b| (3 Marks)
- Make x the subject of the formula in
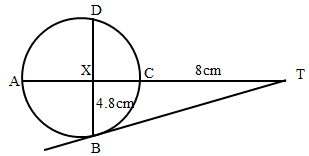
Hence find the value of x when a = 2 and b = 6. (4 Marks) - In the figure below, BT is a tangent to the circle at B. AXCT and BXD are straight lines. AX = 6cm, CT = 8cm, BX = 4.8cm and XD = 5cm. (Figure not drawn to scale)
Find the length of- XC (2 Marks)
- BT (2 Marks)
- Simplify 3 + 1 leaving your answer in the form a + b√c, where a, b and c are rational numbers.
√5-2 √5
(3 Marks) - A quantity y varies partly as another quantity x and partly as the square of x. When x = 20, y = 45 and when x = 24, y = 60.
- Express y in terms of x (3 Marks)
- Find x when y = 75 (1 Mark)
- Expand (a-x)6 upto the term in(x)3. Use your expansion to estimate the value of (2.99)6 to 3 decimal places. (4 Marks)
- A pipe 3.0m long was cut into three pieces. The first piece and the second one were measured as 1.3m and 0.94m respectively. Find the limits within which the length of the third piece lies. (3 Marks)
- A coffee blender has two brands of coffee, Tamu and Chungu. A kilogram of Tamu costs Sh. 70 while a kilogram of Chungu costs Shs. 64. In what ratio should he mix the two brands to make a blend which costs Shs. 68 per kilogram? (2 Marks)
- Find the centre and radius of a circle whose equation is x2+ y2+ 8x + y2 – 2y – 1 = 0 (3 Marks)
SECTION II (50 Marks):
Answer ANY FIVE questions in this section in the spaces provided.
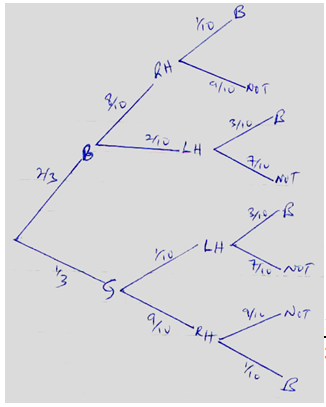
- In a Science class 2/3 of the class are boys and the rest are girls. 80% of the boys and 90% of the girls are right handed. The probability that the right handed student will break a test tube in any session is 1/10 and that for the left handed student is 3/10,regardless of whether boy or girl.
- Draw a tree diagram to represent this information. (2 Marks)
- Using the tree diagram drawn, find the probability that:
- A student chosen at random from the class is left handed (2 Marks)
- A test tube is broken by a left handed student. (2 Marks)
- A test tube is broken by a right handed student. (2 Marks)
- A test tube is not broken in any session (3 Marks)
- Matrix P is given by
- Find P-1 (2 Marks)
- Two institutions, Katulani High School and Nthia High School purchased beans at Sh. b per bag and maize at Sh. m per bag. Katulani purchased 8 bags of beans and 14 bags of maize for KSh. 47,600. Nthia purchased 10 bags of beans and 16 bags of maize for KSh. 57,400.
- Form a matrix equation to represent the information above. (2 Marks)
- Use matrix P-1 to find the prices of one bag of each item. (3 Marks)
- The price of beans later went up by 5% and that of maize remained constant. Katulani bought the same quality of beans but spent the same total of money as before on the two items. State the new ratio of beans to maize. (3 Marks)
- James’ earning are as follows:-
Basic salary Sh. 38,000 p.m
House allowance Sh. 14,000 p.m
Travelling allowance Sh. 8,500 p.m
Medical allowance Sh. 3,300
The table for the taxable income is as shown below.
Income tax in K£ p.a Tax in Sh. per pound 1-600
6001-12000
12001-18000
18001-24000
24001-30000
30001-36000
36001-42000
42001-48000
Over 480002
3
4
5
6
7
8
9
10- Calculate James’ taxable income in K£ p.a. (2 Marks)
- Calculate James’s P.A.YE if he is entitled to a tax relief of Sh. 18000 p.a. (4 Marks)
- James is also deducted the following per month:-
NHIF Sh. 320
Pension scheme Sh. 1000
Co-operative shares Sh. 2000
Loan repayment Sh. 5000
Interest on loan Sh. 500- Calculate James’ total deduction per month in KSh. (2 Marks)
- Calculate his net salary per month (2 Marks)
- Three consecutive terms of a geometric progression are 3(2x+1), 9x and 81 respectively.
- Calculate the value of x (3 Marks)
- Find the common ratio of the series. (1 Mark)
- Calculate the sum of the first 4 terms of this series. (3 Marks)
- Given that the fifth and the seventh terms of the G.P form the first two consecutive terms of an arithmetic sequence, calculate the sum of the first 20 terms of the sequence. (3 Marks)
- A tank has two inlet taps P and Q and an outlet tap R. When empty, the tank can be filled by tap P alone in 4½ hour or by tap Q alone in 3 hours. When full, the tap can be emptied in 2 hours by tap R.
- The tank is initially empty. Find how long it would take to fill up the tank
- If tap R is closed and taps P and Q are opened at the same time. (2 Marks)
- If all the three taps are opened at the same time. (2 Marks)
- The tank is initially empty and the three taps are opened as follows:-
P at 8.00 a.m.
Q at 8.45 a.m
R at 9.00 a.m- Find the fraction of the tank that would be filled by 9.00 a.m (3 Marks)
- Find the time the tank would be fully filled up (3 Marks)
- The tank is initially empty. Find how long it would take to fill up the tank
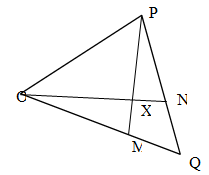
- In the figure below M and N are points on OQ and QP such that OM:MQ = 2:3 and QN : NP = 2:1. ON and PM intersect at X.
- Given that OP = p and OQ = q. Express in terms of p and q
- ON (2 Marks)
- PM (2 Marks)
- Given that OX = hON and PX = kPM where h and k are scalars,
- Determine the values of h and k. (5 Marks)
- Determine ratio in which X divides PM. (1 Mark)
- Given that OP = p and OQ = q. Express in terms of p and q
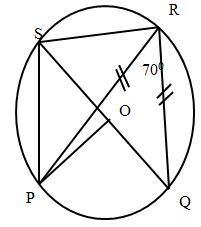
- The figure below shows a circle centre O, PQRS is a cyclic quadrilateral and QOS is a straight line.
Giving reasons for your answers, find the size of- Angle PRS (2 Marks)
- Angle POQ (2 Marks)
- Angle QSR (3 Marks)
- Reflex angle POS (3 Marks)
-
- Complete the table below for y = x3 + 4x2 – 5x – 5 (2 Marks)
x −5 −4 −3 −2 −1 0 1 2 y = x3 + 4x2 – 5x – 5 19 –5 - On the grid provided, draw the graph of y = x3 + 4x2 – 5x – 5 for –5 ≤ x ≤ 2 (3 Marks)
-
- Use the graph to solve the equation x3 + 4x2 – 5x – 5 = 0 (2 Marks)
- By drawing a suitable straight line on the graph, solve the equation (3 Marks)
x3 + 4x2 – 5x – 5 = – 4x – 1
- Complete the table below for y = x3 + 4x2 – 5x – 5 (2 Marks)

MARKING SCHEME
- No. Log
0.7214 2.8582
20.37 0.3090
1.1672 x 1/3
69.8 1.7224
1.8439
3.8785
7.560 x 10-3 - Co-ordinates of mid-point M:
OM = ½(OP + OQ)
=½(-2 8 + (4 7 )) = 1/2 (2, 1.5 ) = (1,7.5 )
Hence M (1,7.5)
Gradient of PQ = 7−8 =−1
4−−2 6
Equation of bisector of PQ at
y−7.5 = 6
x−1
y−7.5 = 6x− 6
y = 6x + 3/2 - A.S.F = 36/49, L.S.F = 6/9 = 2/3
V.S.F = 23 = 8/27
33
8/27 = 20.2/V
v = 68.175cm3 - 87/100 x 800 = 696 (selling point)
B.P x 120/100 = 696, B.P = KSh. 580 -
For ✔ y < x + 4 plotting & shading
For ✔ Plotting & shading y ≤ 6 – x
For ✔ plotting y ≥ 2
For ✔ identification of R
= 1/3x 100 = 331/3% increase- Log (5x + 75) – Log (2x – 9) = Log32
Log (5x+75) = Log32
(2x+9)
5x+75 = 9
2x+9
5x + 75 = 9(2x – 9)
156 = 13x
x = 12 - 2a = 2(3i – 2j + 3k
= 6i – 4j + 6k
3b = 3(2i – 4j – 3k)
= 6i – 12i – 9k
2a – 3b = 8j + 15k
|2a – 3b| = √(64+225)
= 17 - A3 = bx
b+x
A3b + A3x = bx
x(b – A3) = A3b
x = A3b
b-A3
Substituting for A = 2 and b = 6,
23 x 6 = 48
6−23 −2
= −24 -
- 6(XC) = 5 x 4.8
XC = 5 x 4.8 = 4cm
6 - 8 x (8 + 4 + 6) = BT2
BT = √144 = 12cm M1
- 6(XC) = 5 x 4.8
- Adding: 3√5+√5−2 = 2√5−2
√5 (√52) 5−2√5
Multiply by conjugate:-
2√5−2 ∙ 5+2√5
5−2√5 5+2√5
= 10√5+20−10−4√5
25−20
= 6√5/5 +10
2 + 6/5√5 -
- y = kx + cx2
45 = 20k + 400c
60 = 24k + 576c
270 = 120k + 2400c
300 = 120k + 2880c
c = 30/480 = 1/16
45 = 20k + 400/16, k = 1
hence
y = x + 1/16x2 - 75 = x + x2
16
x2 + 16x – 1200 = 0
x = –16√(256+4x1200)
2 x 1
x = −43.56 or 27.56
- y = kx + cx2
- (a−x)6 = a6 + 6a5(−x)1 + 15a4(−x)2 + 20a3−x)3
a6 – 6a5x + 15a4x2 – 20a3x3
(a – x)6 = 2.996 = (3-0.01)6
a = 3, x = 0.01
hence
36 – 6 x 35x (0.01) + 15 x 34 (0.01)2 – 20 x 33 x (0.01)3
729 – 14.58 + 0.1215 – 0.00054
= 714.54096
= 714.541 - Third piece
Max length: 3.05 – (1.25 + 0.935)
= 0.865m
Min length: 2.95 (1.35 + 0.945)
= 0.655m
Hence
0.655 to 0.865m B1 - 1kg of Tamu mixed with x kg of Chungu
(70 x 1) + (64 x x) = 68 x (1 + x)
70 + 64x = 68 + 68x
x = ½
Tamu: Chungu = 1: x = 1:½ - x2 + 8x + (8/1)2 + y2 −2y + ((−2/2)2
= 1 + (8/2)2 + (−2/2)
(x + 4)2 + (y – 1)2 = 18
Centre of circle (−4, 1)
Radius of circle = √18
or 4.243 -
-
- = 2/3 x 2/10 + 1/3 x 1/10
= 4/30 + 1/30 = 5/30 = 1/6 - 2/3 x 2/10 x 3/10 + 1/3 x 3/10 ×1/10
= 12 + 3
300 300
= 15
300
= 1/20 - 2/3 x 8/10 x 1/10 + 1/3 x 9/10 ×1/10
= 16 + 9
300 300
= 25
300
=1/12 - 2/3 x 8/10 x 9/10 + 2/3 x 2/10 x 7/10 +1/3 x 9/10 ×9/10 +1/3 x 1/10 ×7/10
=144 + 28 + 81 + 7
300 300 300 300
= 260
300
=13/15
- = 2/3 x 2/10 + 1/3 x 1/10
-
- Det = 32 – 35
= – 3
P–1 = –1/3 (8 –7 –5 4 ) -
- 8b + 14m = 47600
10b + 16m = 57400
(8 14 10 16 )(b m,) = (47600 57400 )
or
(4 7 5 8 )(b m ) = (23800 28700 ) - (b m ) = ((–8/2 7/3 5/3 –4/3 )(23800 28700 )
(b m ) = (–8/3 x 23800+28700x 7/3 5/3 x23800+–4/3 x 28700 )
(b m ) = (3500 1400 )
Bag of beans cost Sh. 3500
Bag of maize cost Sh. 1400
- 8b + 14m = 47600
- 115/100 x 3500 = 4025
8 x 4025 = 32400
47600 – 32400 = 15400
∴1400m = 15400
m = 11 bags
Ratio 8:11
- Det = 32 – 35
-
- = 38000 + 14000 + 8500 + 3300
= 62800
62800 x 12
20
=K£ 37680 p.a. - 1st K£ 600 = 6000 x 2 = 12000
Next £6000 = 6000 x 3 = 18000
Next £6000 = 6000 x4 = 24000
Next £6000 = 6000 x 5 = 30000
Next £6000 = 6000 x 6 = 36000
Next £6000 = 6000 x 7 = 42000
Rem. £ 1680 = 1680 x 8 = 13440
Tax due p.a. = Sh. 175440
Less relief Sh. 18000
Tax paid = Sh. 157440 -
- Tax paid per month = 157440
12
= 13,120
Total deductions
= 13120 + 320 + 1000 + 2000 + 500
= 23940 - Net salary = 62800
− 23900
38,900
- Tax paid per month = 157440
- = 38000 + 14000 + 8500 + 3300
-
- 9x = 81
3(2x+1) 9x
32x = 34
3(2x+1) 32x
3−1 = 34−2x
−1 = 4 − 2x
2x=5
x = 2.5 - Common ratio =
81
35
= 81
243
= 1/3 - a = 32(2.5)+1
= 36
= 729
= 729 x 80/81 x 3/2
= 1080 - 5th term = 729 × (1/3)4
=9
7th term = 729 × (1/3)6
=1
a=9 d=1 − 9 = −8
S20 = 20/2 (2×9 ÷(20−1))−8
=10(18−152) =−1340
- 9x = 81
-
-
- Fraction filled in 1 hr by PtQ
= 2/9 + 1/3 = 5/9
Time taken to fill tank = 9/5 = 14/5 hrs - Fraction filled in 1 hr by P, Q & r
= 5/9 − ½ = 1/18
Time taken to fill = 18/1 = 18 hours
- Fraction filled in 1 hr by PtQ
-
- Fraction filled by 9.00 a.m
P =2/9 x 1 hr = 2/9
Q = 1/3 x 1/4hrs = 1/12
Both P and Q = 2/9 + 1/12
= 11/36 - Fraction to be filled = 25/36
Time taken = 25/36 x 18
= 12½ hrs
Time for tank to fill up
= 0900
1230
2130 hrs or 9.30 p.m
- Fraction filled by 9.00 a.m
-
-
-
- ON = OP + PN
= P + 1/3PQ
= p + 1/3q− 1/3p
= 2/3p + 1/3q - PM = PO + OM
=−p + 2/3q
- ON = OP + PN
-
- OX = hON
= h(2/3 p+1/3 q)
= 2/3hp + 1/3hq
OX = OP + PX
= P + kPM
= P + k (−p + 2/3 q)
= p – kP + 2/5q
= (1 – k)p + 2/5kq
2/3hp + 1/3hq = (1 – k)p + 2/5kq
2/3 h = 1 – k………. (i)
1/3h = 2/5k …………...(ii)
From (ii) h = 6/5k
Subt in (i)
2/3 x 6/5k = 1 – k
k = 5/9
h = 1/3 - PX : XM = 5/9 : 4/9
= 5 : 4
- OX = hON
-
-
- ∠QRS = 90° (Subst. by the remainder)
∠ PRS = 90 – 70 = 20° - ∠POQ = 2 x 70° = 140°
∠at centre is twice ∠ at circumference - ∠RQP = 180-70 = 55°( Base angles of a ∆)
2
∠RQP and ∠PSE are supplementary (cyclic quadrilateral)
∴∠PSR = 180 – 55 = 125°
∠ QSR = 125 – 70
= 55° - ∠PSQ = ∠PRQ = 70°(Subst. by same arc)
∠QSP = ∠SPO = 70°(base angles of isoscles ∆)
Reflex ∠POS = 360 – 40
= 320°
- ∠QRS = 90° (Subst. by the remainder)
-
x −5 −4 −3 −2 −1 0 1 2 y = x3 + 4x2 – 5x – 5 −4 15 19 13 3 –5 −5 9 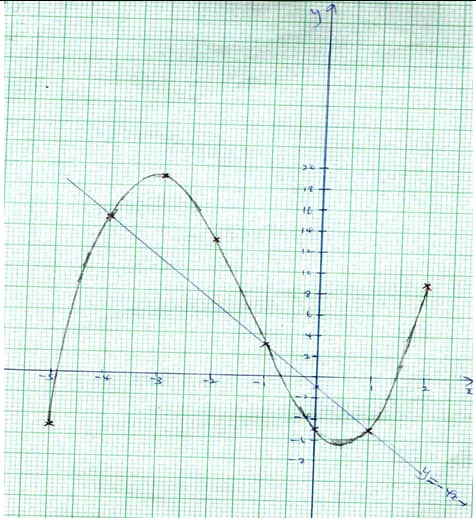
-
- x = -4.85
x = -0.7
x = 1.5 - x3 + 4x2 – 5x – 5 = –4x – 1
x3 + 4x2 – x – 4 = 0
y = x3 – 4x2 – 5x = 5
0 = x3 – 4x2 – x – 4
y = –4x – 1
x = –4x 0 1 y –1 –5
x = 1
- x = -4.85
Download Mathematics Paper 2 Kenya High Post Mock Exams 2020 - Questions and Answers.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students