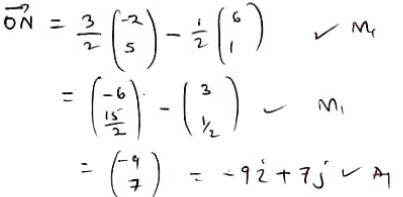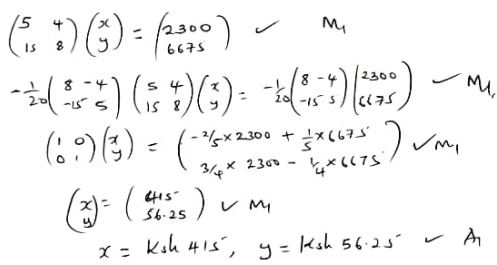- Evaluate −4−4+−15÷5+−3−4÷2 (3 marks)
84÷−7+3−−5 - Simplify completely the expression: 6x2y2−20xy+16 (3 marks)
2x2y2-8 - Given that sin (x + 60)0 = cos (2x), find tan (x + 60)0 (3 marks)
- A triangle whose vertices are P(1, 1), Q(2, 1) and R(1.5, 2) is first rotated about (0, 0) through 1800 followed by an enlargement scale factor 3 with the centre at the origin. Find the co-ordinates of the vertices of the final image. (4 marks)
- List all the integral values of x that satisfy the inequalities; (3 marks)
x−3/2≤2x+1<5 - A bus travelling at an average speed of x km/h left station at 8.15 am. A car, travelling at an average speed of 80km/h left the same station at 9.00 am and caught up with the bus at 10.45 am. Find the value of x. (3 marks)
- Find the size of angle RPQ of a triangle PQR in which PQ = 9 cm, QR = 12 cm and RP = 6 cm (3 marks)
- Use squares, square roots and reciprocals tables to evaluate, to 4 significant figures, the expression: (3 marks)
1 + 3
√27.56 (0.071)2 - From a point 20m away on a level ground the angle of elevation to the bottom of the window is 27° and the angle of elevation of the top of the window is 32°. Calculate the height of the window. (3 marks)
- Solve for x in the equation: 32x+1+4×32x+1− 45 = 0 (3 marks)
- Three spacecrafts in different orbits go around the earth at intervals of 3, 6 and 7 hours respectively. An engineer at an observatory on earth first observes the three crafts cruising above one another at 6.35 a.m. At what time in a similar configuration if the all revolve around the earth from east to west? (3 marks)
- Use the mid - ordinates rule to estimate the area enclosed by the curve y = x2, x-axis and lines x=2 and x=5 using 3 strips (3 marks)
- A piece of wire 18 cm long is to be bent to form a rectangle. If its length is x cm, obtain an expression for its area. Hence calculate the dimensions of the rectangle with maximum area from the expression (4 marks)
- The cost of providing a commodity consists of transport, labour and raw materials in the ratio 8:4:12 respectively. If the transport cost increases by 12%, labour cost by 18% and raw materials by 40%, find the percentage increase of producing the new commodity. (3 marks)
- Vector OP = 6i + j and OQ = − 2i +5j. A point N divides PQ in the ratio 3:−1. Find ON in terms of i and j. (3 marks)
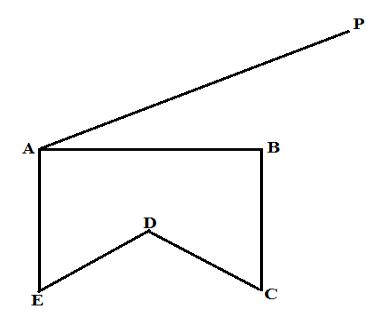
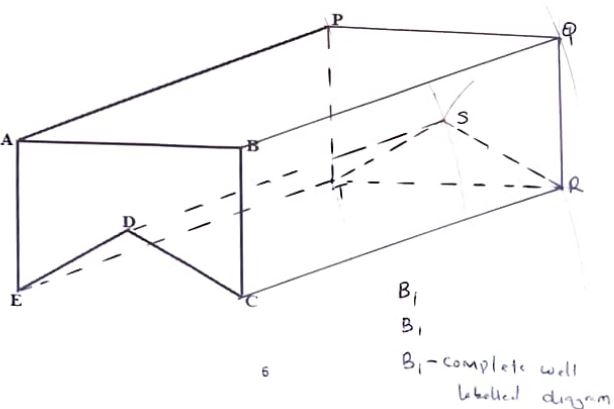
- In the figure below ABCDE is a cross-section of a solid ABCDEPQRST. The solid has a uniform cross-section. Given that AP is an edge of the solid, complete the sketch showing the hidden edges with a broken lines. (3 marks)
SECTION II (50 Marks)
Answer only five questions from this section in the spaces provided.
- A carpenter constructed a closed wooden box with internal measurements 1.5m long, 0.8m wide and 0.4m high. The wood used in constructing the box was 1.0cm thick and had a density of 0.6g/cm3.
- Determine:-
- Volume of the wood used in constructing the box in cm3. (4 marks)
- Mass of the box in kilograms. Give answer to one decimal place. (2 marks)
- Identical cylindrical tins of diameter 10cm, height 20cm with a mass of 120g each, were packed into the box.
Calculate:-- The maximum number of the tins that can be packed. (2 marks)
- The total mass of box and the tins in kg. (2 marks)
- Determine:-
- Two factories A and B produce both chocolate bars and eclairs. In factory A, it costs Kshs x and Kshs y to produce 1 kg of chocolate bars and 1 kg of eclares respectively. The cost of producing 1 kg of chocolate bars and 1 kg of eclairs in factory B increases by the ratio 6:5 and reduce by the ratio 4:5 respectively.
- Given that it costs Kshs 460 000 to produce 1 tonne of chocolate bars and 800kg of eclares in factory A and Kshs 534 000 to produce the same quantities in factory B, form two simplified simultaneous equations representing this information. (3 marks)
- Use matrix method to find the cost of producing 1 kg of chocolate bars and 1 kg of eclaires in factory A. (5 marks)
- Find the cost of producing 100 kg of chocolate bars and 50 kg of eclaires in factory B. (2 marks)
- Two friends Jane and Bob live 40 km apart. One day Jane left her house at 9.00 a.m. and cycled towards Bob’s house at an average speed of 15 km/h. Bob left his house at 10.30 a.m. on the same day and cycled towards Jane’s at an average speed of 25 km/h.
- Determine :
- The distance from Jane’s house to where the two friends met. (4 marks)
- The time they met. (2 marks)
- How far from Jane’s house when they met. (2 marks)
- The two friends took 10 minutes at the meeting point and then cycled to Bob’s house at an average speed of 12 km/h. Find the time they arrived at Bob’s house. (2 marks )
- Determine :
- The masses to the nearest kilogram of some students were recorded in table below.
Mass(kg) 41-50 51-55 56-65 66-70 71-85 Frequency 8 12 16 10 6 0.2 - Complete the table above to 1 decimal place. (2 marks)
- On the grid provided below, draw a histogram to represent the above information. (3 marks)
- Use the histogram to:
- State the class in which the median mark lies. (1 mark)
- Estimate the median mark (2 marks)
- The percentage number of students with masses of at least 74kg. (2 marks)
-
- straight line L1 whose equation is 9y−6x = −6 meets the x-axis at Z. Determine the coordinates of Z (2 marks)
- A second line L2 is perpendicular to L1 at Z. Find the equation of L2 in the form ax + by = c, where ,b and c are integers. (3marks)
- A third line L3 passes through the point (2,5) and is parallel to L1. Find:
- The equation of L3 in the form ax+by=c, where a, b and c are integers. (2 marks)
- The coordinate of point R at which L2 intersects L3. (3 marks)
-
- Complete the table below for the equation y = 2x2 + 3x − 11 (2 Marks)
x −5 −3 −2 −1 0 1 2 3 2x2 32 3x −12 − 11 −11 −11 −11 −11 −11 −11 −11 −11 y - On the grid paper provided draw the graph of y = 2x2 + 3x − 11 (3 Marks)
- On the same axes draw the graph of y = 2x + 1 (1 Marks)
- Use your graph to solve the quadratic
- 2x2 + 3x −11 = 0 (2 Mark)
- 2x2 + x − 12 = 0 (2 Marks)
- Complete the table below for the equation y = 2x2 + 3x − 11 (2 Marks)
- Five points, P, Q, R, V and T lie on the same plane. Point Q is 53km on the bearing of 055° of P. Point R lies 162° of Q at a distance of 58km. Given that point T is west of P and 114km from R and V is directly south of P and S40°E from T.
- Using a scale of 1:1,000,000, show the above information in a scale drawing. (3 marks)
- From the scale drawing determine:
- The distance in km of point V from R. (2 marks)
- The bearing of V from Q. (2 marks)
- Calculate the area enclosed by the points PQRVT in squares kilometers. (3 marks)
- The displacement S of a particle after t seconds is given by S = 4t3 − 5/2t2 − 3t + 3.
Determine the:- velocity of the particle when t = 3 (3 marks)
- value of t when the particle is instantaneously at rest (3 marks)
- displacement when the particle is instantaneously at rest. (2 marks)
- acceleration of the particle when t=2 seconds (2 marks)
- Evaluate −4−4+−15÷5+−3−4÷2 (3 marks)
84÷−7+3−−5
Numerator = −4(−7 −3 −2)
= −4 x −12 = 48
Denominator = −12 + 3 + 5 = −4
= 48
−4 = −12 - Simplify completely the expression: 6x2y2−20xy+16 (3 marks)
2x2y2−8
Numerator = 6x2y2−20xy+16 = (6xy − 8)(xy − 2)
= 6x2y2−12xy−8xy+16 2(xy + 2)(xy − 2)
= 6xy(xy − 2)−8(xy−2) = 3xy − 4
= (6xy − 8)(xy − 2) xy + 2
Denominator = 2x2y2−8
= 2(xy + 2)(xy −2) - Given that sin (x + 60)0 = cos (2x), find tan (x + 60)0 (3 marks)
x + 60 + 2x = 90
3x = 30
x = 10
Tan(10 + 60) = 2.7475 - A triangle whose vertices are P(1, 1), Q(2, 1) and R(1.5, 2) is first rotated about (0, 0) through 1800 followed by an enlargement scale factor 3 with the centre at the origin. Find the co-ordinates of the vertices of the final image. (4 marks)
P1(−1, −1), Q1(2, −1) R1(−1.5, −2) B1B1
P11(−3, −3), Q11(−6, −3) R11(−4.5, −6) B1B1 - List all the integral values of x that satisfy the inequalities; (3 marks)
x−3/2≤2x+1<5
−3/2 ≤ x + 1
_5/2 ≤ x
2x < 4
x < 2
−2½ ≤ x < 2
= −2, −1, 0, 1 all intergral values - A bus travelling at an average speed of x km/h left station at 8.15 am. A car, travelling at an average speed of 80km/h left the same station at 9.00 am and caught up with the bus at 10.45 am. Find the value of x. (3 marks)
Distance covered by gas at 9.00am 45/60 X x = ¾x km
Relative speed = (80 − x)km/h
Catch up time = 10.45
9.00
1¾hrs
Distance = s x t
¾x = 7/4 ( 80 − x)
10/4x = 140
x = 56 - Find the size of angle RPQ of a triangle PQR in which PQ = 9 cm, QR = 12 cm and RP = 6 cm (3 marks)
122 = 92 + 62 − 2 x 9 x 6 Cos P
144 = 117 − 108Cos P
< RPQ = Cos −1 27/−108
= 104.48° - Use squares, square roots and reciprocals tables to evaluate, to 4 significant figures, the expression: (3 marks)
1 + 3
√27.56 (0.071)2
√27.56 = 5.2497
(0.071)2 = (7.1 x 10−2)2 = 50.41 x 10−4
= 1/5.2497 + 3/5.041 x 10−3
= 0.1908 + 3 x 0.1984 x 10
= 595.2 - From a point 20m away on a level ground the angle of elevation to the bottom of the window is 27° and the angle of elevation of the top of the window is 32°. Calculate the height of the window. (3 marks)
Height of the window = 20 tan 32 − 20 tan 27
= 2.30689 - Solve for x in the equation: 32x+1+4×32x+1− 45 = 0 (3 marks)
3.32x + 4.3.32x = 45
15.32x = 45
15 15
32x = 3
2x = 1
x = ½ - Three spacecrafts in different orbits go around the earth at intervals of 3, 6 and 7 hours respectively. An engineer at an observatory on earth first observes the three crafts cruising above one another at 6.35 a.m. At what time in a similar configuration if the all revolve around the earth from east to west? (3 marks)
L.C.M = 2 x 2 x 7
= 42hrs
6.35
42.00
48.35
−24
24.35 = 12.35am on the third day - Use the mid - ordinates rule to estimate the area enclosed by the curve y = x2, x-axis and lines x=2 and x=5 using 3 strips (3 marks)
h = 5 − 1 = 1
3
x 2.5 3.5 4.5 y 6.25 12.25 20.25
A = 1(6.25 + 12.25 + 20.25)
= 38.75sq units - A piece of wire 18 cm long is to be bent to form a rectangle. If its length is x cm, obtain an expression for its area. Hence calculate the dimensions of the rectangle with maximum area from the expression (4 marks)
Width = 18 − 2x
2
= 9 − x
A = x(9 − x)
= 9x − x2
dy/dx = 9 − 2x = 0
x = 4.5cm
width = 9 − 4.5 = 4.5cm - The cost of providing a commodity consists of transport, labour and raw materials in the ratio 8:4:12 respectively. If the transport cost increases by 12%, labour cost by 18% and raw materials by 40%, find the percentage increase of producing the new commodity. (3 marks)
Let the total cost be x
new cost = 8/24x X 112/100 + 4/24x X 118/100 + 12/24x X140/100
= 127x
100
% Increase = 127/100x − x x 100% = 27% Increase
x - Vector OP = 6i + j and OQ = − 2i +5j. A point N divides PQ in the ratio 3:−1. Find ON in terms of i and j. (3 marks)
- In the figure below ABCDE is a cross-section of a solid ABCDEPQRST. The solid has a uniform cross-section. Given that AP is an edge of the solid, complete the sketch showing the hidden edges with a broken lines. (3 marks)
SECTION II (50 Marks)
Answer only five questions from this section in the spaces provided.
- A carpenter constructed a closed wooden box with internal measurements 1.5m long, 0.8m wide and 0.4m high. The wood used in constructing the box was 1.0cm thick and had a density of 0.6g/cm3.
- Determine:-
- Volume of the wood used in constructing the box in cm3. (4 marks)
Internal volume = 150 x 80 x 40 = 480,000cm3
External volume = 152 x 82 x 42 = 523,488cm3
Volume of the wood = 523,488 − 480,000
= 43,488cm3 - Mass of the box in kilograms. Give answer to one decimal place. (2 marks)
M = V X D
= 43,488 X 0.6 = 26092.8g
= 26.1kg
- Volume of the wood used in constructing the box in cm3. (4 marks)
- Identical cylindrical tins of diameter 10cm, height 20cm with a mass of 120g each, were packed into the box.
Calculate:-- The maximum number of the tins that can be packed. (2 marks)
150/10 x 80/10 x 40/20
= 480 tins - The total mass of box and the tins in kg. (2 marks)
= 120 x 480 + 26.0928
1000
= 83.6928kg
- The maximum number of the tins that can be packed. (2 marks)
- Determine:-
- Two factories A and B produce both chocolate bars and eclairs. In factory A, it costs Kshs x and Kshs y to produce 1 kg of chocolate bars and 1 kg of eclares respectively. The cost of producing 1 kg of chocolate bars and 1 kg of eclairs in factory B increases by the ratio 6:5 and reduce by the ratio 4:5 respectively.
- Given that it costs Kshs 460 000 to produce 1 tonne of chocolate bars and 800kg of eclares in factory A and Kshs 534 000 to produce the same quantities in factory B, form two simplified simultaneous equations representing this information. (3 marks)
1000x + 800y = 460,000
5x + 4y = 2300
In factor B
Cost of 1kg of chocolate = 6/5x
Cost of 1kg of eclairs = 4/5y
1000 x 6/5x + 800 x 4/5y = 534000
15x + 8y = 6675 - Use matrix method to find the cost of producing 1 kg of chocolate bars and 1 kg of eclaires in factory A. (5 marks)
- Find the cost of producing 100 kg of chocolate bars and 50 kg of eclaires in factory B. (2 marks)
6/5 x 415 x 100 + 4/5 x 50 x 56.25
= ksh 52,050
- Given that it costs Kshs 460 000 to produce 1 tonne of chocolate bars and 800kg of eclares in factory A and Kshs 534 000 to produce the same quantities in factory B, form two simplified simultaneous equations representing this information. (3 marks)
- Two friends Jane and Bob live 40 km apart. One day Jane left her house at 9.00 a.m. and cycled towards Bob’s house at an average speed of 15 km/h. Bob left his house at 10.30 a.m. on the same day and cycled towards Jane’s at an average speed of 25 km/h.
- Determine :
- The distance from Jane’s house to where the two friends met. (4 marks)
Distance covered by Jane at 10.30 am = 15 x 1.5 = 22.5hk
Distance between them at 10.30 am = 40 − 22.5 = 17.5km
Relative speed = 15 + 25 = 40km/hr
Time taken before the met = 17.5/40 = 7/16 hrs
Distance from Jane's house = 22.5 + 7/16 x 15 = 29.0625km - The time they met. (2 marks)
= 10.30
26.15
10.56.15 am - How far from Bob's house when they met. (2 marks)
40 − 29.062 = 10.938
- The distance from Jane’s house to where the two friends met. (4 marks)
- The two friends took 10 minutes at the meeting point and then cycled to Bob’s house at an average speed of 12 km/h. Find the time they arrived at Bob’s house. (2 marks )
T = D/S = 10.938/12 = 54min 41 seconds
= 10.56.15
10
54.41
12.00.56 am
- Determine :
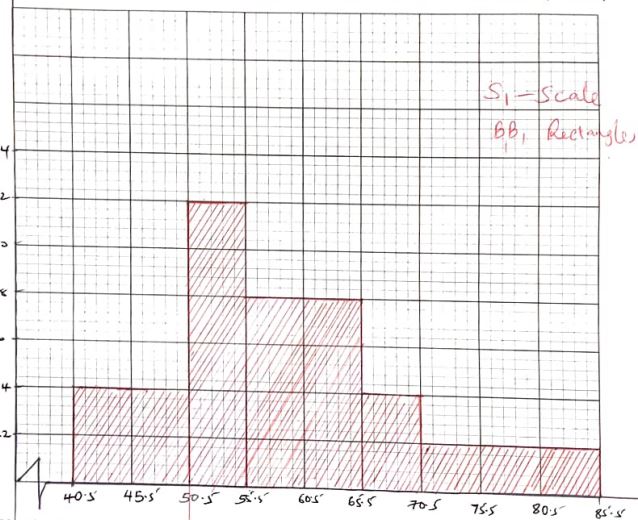
- The masses to the nearest kilogram of some students were recorded in table below.
Mass(kg) 41-50 51-55 56-65 66-70 71-85 Frequency 8 12 16 10 6 0.4 1.2 0.8 1.0 0.2 - Complete the table above to 1 decimal place. (2 marks)
- On the grid provided below, draw a histogram to represent the above information. (3 marks)
- Use the histogram to:
- State the class in which the median mark lies. (1 mark)
56 - 65 - Estimate the median mark (2 marks)
55.5 + 6 = 59.25
2 x 0.8 - The percentage number of students with masses of at least 74kg. (2 marks)
5/26 x 100% = 8.929%
- State the class in which the median mark lies. (1 mark)
-
- straight line L1 whose equation is 9y−6x = −6 meets the x-axis at Z. Determine the coordinates of Z (2 marks)
− 6x = − 6
x = 1
Z(1, 0) - A second line L2 is perpendicular to L1 at Z. Find the equation of L2 in the form ax + by = c, where ,b and c are integers. (3marks)
L1 y = 2/3x − 6
L2 y − 0 = −3
x − 1 2
y = −3/2x + 3/2
3x + 2y = 3 - A third line L3 passes through the point (2,5) and is parallel to L1. Find:
- The equation of L3 in the form ax+by=c, where a, b and c are integers. (2 marks)
y − 5 = 2
x − 2 3
y − 5 = 2/3x − 4/3
2x − 3y = −11 - The coordinate of point R at which L2 intersects L3. (3 marks)
3x + 2y = 3
2x − 3y = −11
6x + 4y = 6
6x − 9y = −33
13y = 39
y = 3
x = −1
R(−1, 3)
- The equation of L3 in the form ax+by=c, where a, b and c are integers. (2 marks)
- straight line L1 whose equation is 9y−6x = −6 meets the x-axis at Z. Determine the coordinates of Z (2 marks)
-
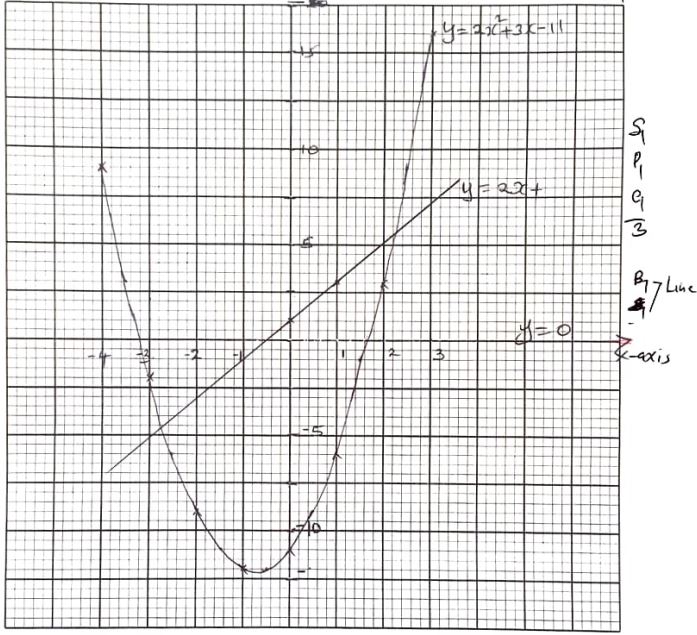
- Complete the table below for the equation y = 2x2 + 3x − 11 (2 Marks)
x −5 −3 −2 −1 0 1 2 3 2x2 32 18 8 2 0 2 8 18 3x −12 −9 −6 −3 0 3 6 9 − 11 −11 −11 −11 −11 −11 −11 −11 −11 y −9 −2 −9 −12 − 11 − 6 3 16 - On the grid paper provided draw the graph of y = 2x2 + 3x − 11 (3 Marks)
- On the same axes draw the graph of y = 2x + 1 (1 Marks)
- Use your graph to solve the quadratic
- 2x2 + 3x −11 = 0 (2 Mark)
X = −3.2 OR X =1.7 - 2x2 + x − 12 = 0 (2 Marks)
Y = 2x2 + 3x − 11
0 = 2x2 + x − 12
y = 2x + 1 x = −2.7 or 2.3
- 2x2 + 3x −11 = 0 (2 Mark)
- Complete the table below for the equation y = 2x2 + 3x − 11 (2 Marks)
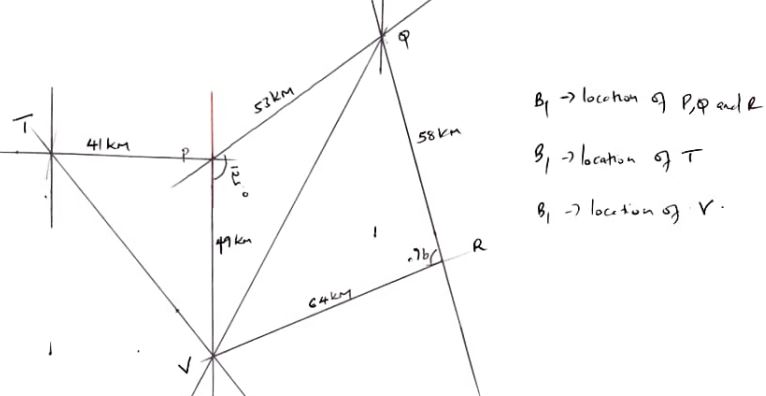
- Five points, P, Q, R, V and T lie on the same plane. Point Q is 53km on the bearing of 055° of P. Point R lies 162° of Q at a distance of 58km. Given that point T is west of P and 114km from R and V is directly south of P and S40°E from T.
- Using a scale of 1:1,000,000, show the above information in a scale drawing. (3 marks)
- From the scale drawing determine:
- The distance in km of point V from R. (2 marks)
6.4 x 10 = 64km - The bearing of V from Q. (2 marks)
029° + 180 = 209° - Calculate the area enclosed by the points PQRVT in squares kilometers. (3 marks)
= ½ x 41 x 49 + ½ x 53 x 49Sin125 + ½ x 64 x 58Sin96
= 3914 km
- The distance in km of point V from R. (2 marks)
- Using a scale of 1:1,000,000, show the above information in a scale drawing. (3 marks)
- The displacement S of a particle after t seconds is given by S = 4t3 − 5/2t2 − 3t + 3.
Determine the:- velocity of the particle when t = 3 (3 marks)
V = 12t2 − st − 3
at t = 3
V = 12(3)2 − 5(3) − 3
= 90 m/s - value of t when the particle is instantaneously at rest (3 marks)
12t2 − st − 3 = 0
12t2 − 9t + 4t − 3 = 0
3t(4t − 3) + (4t − 3) = 0
(3t + 1)(4t − 3) = 0
3t + 1 = 0
t = − 1/3 or
4t − 3 = 0
t = ¾ seconds - displacement when the particle is instantaneously at rest. (2 marks)
s = 4(¾)3 − 5/2(¾)2 − 3 x (¾) + 3
= 11/3 - acceleration of the particle when t=2 seconds (2 marks)
a = 24t − 5
= 24(2) − 5
= 43m/s2
- velocity of the particle when t = 3 (3 marks)
Download Mathematics Paper 1 Questions and Answers - Lugari Constituency Joint Pre Mock Exams 2023.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students