Mathematics Paper 2 Questions and Answers - Lugari Constituency Joint Pre Mock Exams 2023

1. Use logarithm tables to evaluate to 4 significant figures  (4mks)
   (90.35 +         1    )^1/3 
                  0.03506             
2. Simplify  3    +  4 −√2.  Write your answer in the form a+ b√C (3mks) 
               2+√2     2−√2
3. The following are ages of students in a class 7,9,8,9,11,12,10 9,8,6,7,10,11,12,6,9,7, and 11.
   1. Complete the frequency distribution table below (1 mark)
      
      

      Ages	6	7	8	9	10	11	12
      No of students

   2. Calculate the variance  of their ages in five years’ time.    (2 marks)
4. Expand (p - 3q )⁵               (1mks)
   hence state
   1. Coefficient of p⁴q        (1mks)
   2. Fourth term in the expansion    (1mk)
5. Make c the subject of the formula  b = √k − ac ,   hence find the value of c when k= 1, a=4 and b= 2           (3mks)
6. Given that A= (3x x − 36 − 62x −2)   Find value of x such that A is a singular matrix.    (3mks)
7. The points O, A and B have the coordinates (0, 0), (4, 0) and (3, 2) respectively. Under a shear represented by the matrix , triangle OAB maps onto triangle OAB’.
   1. Determine in terms of k, the x coordinates  of point B’. {1 mark}
   2. If OAB’ is a right angled triangle in which angle OB’A is acute, find two possible values of k. {2 marks}
8. Find the value of t if the gradient of the graphs of the functions y = x² − x³ and y = x − tx² are equal at  x = ¹/₃. (3marks)
9. The  cash price of a TV set is Ksh 13800.  A customer opts to buy the set on hire purchase   terms by paying a deposit of Ksh. 2280.  If the simple interest of 20% p.a is charged on the   balance and customer is required to pay 24 equal monthly instalments calculate the amount of each instalment. (  3mks)
10. Solve the equation
    Log² (2 +3x) + 3log₂ 2 = 2+log₂ (2x+6) (3mks)
                                                                                                                AB   
11. Given that 2 ≤ A ≤ 4 and 0.1 ≤ B ≤ 0.2.  Find the minimum value of A − B.(3 marks)
12. Chords PQ and RS intersect internally at point T.  Given that PT = 3.2 cm, TQ= 4.7cm and TS = 5.2cm, find the length of chord RS.     (3mks)
13. Two taps A and B can fill a water bath in 8 minutes and 10 minutes respectively. Tap A is opened for 2 minutes then closed. Tap B is later opened for one minute then closed. How long will the two taps take running together to fill the remaining part of the water bath?  (3marks)
14. On the line AB below show by shading the region R above the line such that
    1. R is nearer A than B                                                 
    2. R is not more than 3.0 cm from A        (4mks)
    3. < ARB 90° 
       A __________________________ B
15. Determine the radius and centre of a circle whose equation is
    3x² +3y²–18x+12y−9=0 (3mks)
16. Solve the equations for values of θ from 0° to 360°. {4 marks}
                       7   
    3tan2θ − Cosθ + 5 = 0

SECTION II (50 MARKS)

ANSWER ONLY FIVE QUESTIONS IN THIS SECTION

17.  
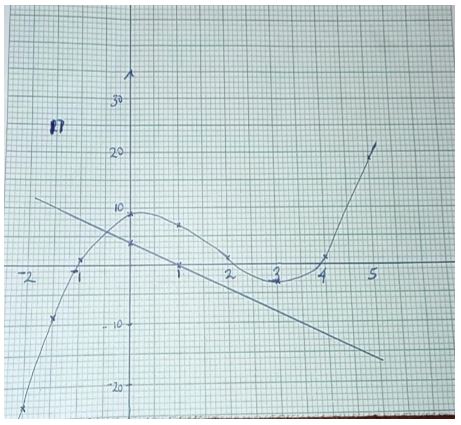
    1. Complete the table below for values of y for the curve   (2mks)
       Y= x³−5x²+2x+9 for −2≤ x ≤5
       

       x	−2	−1.5	−1	0	1	2	3	4	5
       y

    2. Draw a graph of y= x³−5x²+2x+9 for −2 ≤ x ≤ 5 (3mk)
       
    3. Use your graph to solve the equations
       1. X³−5x²+2x+9 = 0   (2mks)
       2. X³−5x²+6x = −5           (3 mks)
18. The cost Y of producing a number of items varies partly as X and partly inversely as X.  To  produce 2   items it costs sh. 135 and to produce 3 items it costs sh.140.
    1. Find the  Law connecting Y and X. (5mks)
    2. Cost of producing 10 items. (2mks)
    3. Number of items produced at  a cost of sh.180 (3mks)
19. The first, fourth and thirteenth terms of an AP correspond to the first three consecutive terms of an increasing Geometric progression.
    Given that the first term of the AP is a and common difference is d
    1. Write down the first three terms of the GP in terms of a and d. (1mk)
    2. The sum of the third and eleventh terms of the AP is 30.
            Calculate;
       1. The first term and common difference of the AP (5mks)
       2. Common ratio of the GP (2mks)
       3. Sum of the first 10 terms of the GP (2mks)
20.  
    1. Two towns on latitude 30° N are 3000km apart. Find the longitude difference of the two Towns. (Take π  = ²²/₇ and radius of earth to be 6370km) (2mks)
    2. The position of the airport P and Q are P (60°N, 45°W)  and Q (60°N, K°E)
       It takes a plane 5 hrs to travel due East from P to Q at an average speed of 600 knots.
       1. Calculate the value of K (3mks)
       2. The local time at P is 10.45 am when is the local time at Q when the plane reached there? (3mks)
    3. Calculate the shortest distance between A(30°S, 36°E) and B (30°S, 144°W) (2mks)
21. The probability that Andrew goes to bed on time is ²/₃.  If he goes to bed on time the probability that he wakes up early is ³/₅ otherwise it is ¹/₇. If Andrew wakes up late, the probability that he will be punctual for class is ¹/₄ otherwise its is ²/₇. 
    1. Draw  a tree diagram to represent above the information. (2mks)
    2. Determine the probability that;
       1. He will wake up late (2mks)
       2. He will wake up early and arrive in class late (2mks)
       3. He will go to bed late but arrive class early (2mks)
       4. He will be late for class. (2mks)
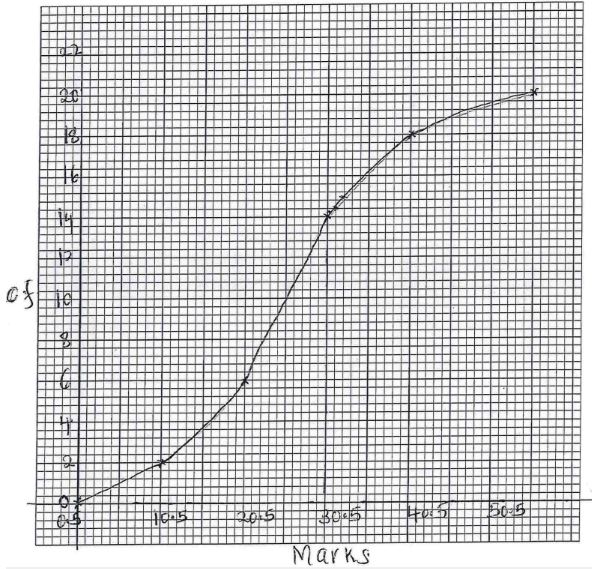
22. The table below shows the frequency distribution of marks scored by students  in a  test.
    

    MARKS	1-10	11-20	21-30	31-40	41-50
    FREQUENCY

    
    
    1. On the grid provided, draw a cumulative frequency curve for the data. (3 marks)
       
    2. Use your graph to determine;
       1. The pass mark if only 6 students passed the exam.            (2 marks)
       2. The upper quartile mark          (1 mark)
    3. Find the percentage change if the upper quartile in b(ii) above was found by calculation.  (3 marks)                                                   
23. A transport company runs a fleet of two types of busses operating between Meru and Nairobi.Coach buses and Minibuses.   A coach bus carries 52 passengers and 200kg of luggage while a minibus carries 32 passengers  and 300kg of luggage. On one Saturday, there were 500 passengers with 3500 kg of luggage to be transported, the company could only use a maximum of 15 buses all together.
    1. if the company uses x coach buses and y minibuses write down all  inequalities that satisfy the given conditions. (4mks)
    2. Represent the inequalities graphically in the grid provide (use a scale of 1cm to represent 1 unit) (3mks)
                                                   
    3. if the cost of running one coach bus is sh.7200 and that of running one minibus is sh. 6000. use the graph above to determine the minimum cost of running the vehicles  (3 mks)
24. The velocity of a particle after t seconds is given by V= t² – 4t+4.
    1. Find displacement of the particles during the third second (4mks)
    2. Determine the time when the particle is momentarily at rest (3mks)
    3. The acceleration of the particle after 2 seconds (3mks)                                                                                         

	MARKING  SCHEME
	WORKING	MARKS
1	No.                 Log              1.000------    0.0000   0.03506---    2.5448   28.5 -------    1.4552          +   90.35   118.87------  2.0751÷3   4.917×10°   0.6917   4.917	M1   M1     M1 A1 4MKS
2	3 + 4 + 4−√2   2+√2    2-√2   = 3(2−√2)+(4-√2)(2+√2)            (2+√2)(2−√2)  = 63√2+8+4√2−2√2−2                 4−2  = 12-√2         2	M1     M1   A1 3MKS
3	(p-3q)5 = p5+5p4(−3q)−10p3(−3q)2+10p2(−3q)3  = p5  +−15p4q +90p3q2 -270p2q3  (i)  Coefficient =-15  (ii) 4th term =– 270p2q3	B1 B1 B1       3 MKS
4	b = √k – ac  b2 = k − c  c = k − b2           a  c = 12−22  = − 3            4           4	M1 M1 A1   3 MKS
5	(3x x−6 )   −6 2x−2  D = 3x(2x-2) −6(x-6) = 0     = 6x2−6x−6x+6 = 0     = 6x2−12x+6 = 0     = 6x2−6x−6x+6 = 0        6x(x−1)−6(x−1) = 0      = x−1(6x−6)=0       X = 1	M1 M1 A1          3MKS
6	x (x+3) −12 = 0  x2 + 3x−12 = 0  x2+ 4x−x −12 = 0  x(x+4)−1(x+4) = 0  (x-1)(x+4) = 0  X = 1 x = −4	M1 M1   A1  3MKS
7	(a) When a shear transformation is applied to a point (x, y) using the matrix (1, k, 0, 1), the resulting coordinates are:         x' = x + ky         y' = y       In this case, we have point B with coordinates (3, 2). After applying the shear transformation, the coordinates of B' will be:      x' = 3 + k * 2      y' = 2      Simplifying the x-coordinate in terms of k:       x' = 3 + 2k       So, in terms of k, the x-coordinate of point B' is 3 + 2k
8		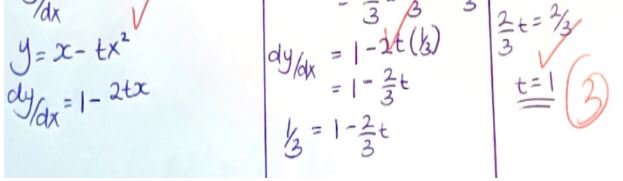M1 M1     A1  3MKS
9	147  >> 105%  Cp  = 100105 x 147 = sh 140  Let the ratio b 1: n  =  100x1+150n  140           1+n  100 +105n = 140 + 140n  10n = 40  n =4  ratio 1⋮4	M1 M1 M1 A1
10	Log2 (2+3x) + 3log22 = 2+ log2 (2x +6)  Log (  2 +3x)23 )  = log ( 22 (2x +6)  4+6x = 2x +6   4x = 2  X = 0.5          or  Log28(2+3x)  = log24(2x+6)  16 +24x = 8x + 24  16x = 8  X= ½	B1    B1 B1 B1
11	2(0.1) = 0.2   4 − 0.1   3.9   0.2 = 2   3.9   39	B1     M1     A1       3MKS
12	5.2(RT) = 3.2x4.7  RT = 3.2 x 4.7              5.2            = 2.59     RS = 5.2 + 2.89           = 8.09	M1   M1 A1 3MKS
13	A - 8 minutes,  B  =  10 minutes  In one minute  A 1/8, in one minute B 1/10, Fraction filled up  1/4+1/10 = 7/20  Tap A and B combined 1/8  +1/10 = 9/40  13/20 − 40/9 = 26/9   2, 8/9	B1   M1 A1   3MKS
14	Seeing the factions For perpendicular bisector Circle centre ASemicircle Shaded region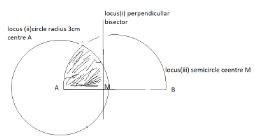	B1       B1 B1 B1
15	3X2 + 3Y2 –  18X + 12Y – 9 =0  X2 + Y2 -6X +4Y = 0  X2 − 6X + 9 + Y2 + 4Y + 4 = 3 + 9 + 4  (X - 3)2 + (Y + 2)2 = 16  Centre (3,-2)   Radius = 4	B1 B1 B1         3mks
16	240   =    b       sin45   sin105  b = 240 x sin105       sin45  327.8461	B1   M1 A1        3mks
	SECTION II
17	x       −2    −1.5       −1         0          1            2            3            4           5  y	B2           S1     P1   A1
18	(i) Y = nX + m/X      Y = nX + m/X     135 = 2n + m/2    140 = 3n + m/3    4m + n = 270    9m + n = 420    5m   = 150  (ii) M = 30      n = 270−120 =150  (iii) y = 30x + 150/x           = 315    y = 30x10 +  150/10      = 315    30x +  150/x = 180   30 x2 +150 =180x   30 x2 – 180x +150 = 0   (x-5)(x-1)= 0   X=5 or x=1	M1     M1 A1 B1 B1    M1 A1   M1       M1 A1  10mks
19	(a) a  a+3d  a+ 12d  (b) (i)     a+ 2d + a+ 10d =30      2a + 12a =30     a+3d   =   a+12d        a            a+3d     (a+3d )2    = a2  + 12ad    9d2 -6ad + 9d2 = a2 +12ad    9d2 – 6ad =0    9d2- 90d(15-6d) = 0      9d2 -90d +36d2 = 0    45 d2 + 90d = 0    9d (5d - 10)= 0    d = 0 or d= 2    a =  15-6d      = 15-12    (ii) = 3    (iii) r  = a+ 3d  =  3+6                   a            3                         =  3         S10 = 3(310 −1) / 2  =  888572	B1     M1           M1   M1 A1   A1   M1 A1 M1A1 10mks
20	(a)  Dist AB = α/360  x  2πR Cos        3000 = α/360  x  2 R Cos30          Α  =  31.15°   (b) 60α cos  = 5x600      α =  50/cos60         = 1000      K   =  100 – 45          = 55°        Long diff = 450 + 550 =900    Time diff = 100  x4 / 60                 = 6hrs 40mins   Time at Q = 10.45am + 6hrs 40 mins                   17 25 HRS   Time when the plane reached  17 25hrs + 5 hrs                                 22 25 HRS	M1  A1                                     10mks
21	(i) P(wakes up early) = p(BE’ or B’ E’)                                   = 2/3  x  2/5 + 1/3 x 6/7                                     = 11/14 (ii) P(wakes up early but late for class)= P(BEC’ or B’ EC’)                                   = 2/3 x 2/5 x 5/7 + 1/3 x 1/7 x 5/7                                   = 26/147 (ii) P(bed late but early for class) = P(B’EC or B’ E’C)                                      = 1/3  x 1/7 x 2/7 + 1/3 x 6/7 x 1/4                                   =  25/294      P(late) =   P(BEC ‘or B E’C’ or B’EC’ or B’E’C’)       =   23   x 35 x 5 7   +   13   x  17  x   57  +  23   x 25 x 3 4   +    13   x  67  x   34        =12891470	M1 A1     M1   A1   M1 A1     M1 A1   10mks
22	(a)  (b) (i) The pass mark if 6th                  20−6 = 14th                   30.5 marks       (ii) Upper quartile  marks                 0.75 x50 = 31.5 Marks                   15th value (c) 30.5 + (15−14 )10 = 30.5+2.5 = 33                       4                 33−31.5 = 4.76                   31.5	B1          S1   P1 C1                     M1   A1     B1   M1 M1   A1   10mks
23	(a) 52x + 32y ≥ 500       13x + 8y ≥ 125………………………………………1        200x + 300y ≥ 3500        2x + 3y ≥ 35…………………………………………..2        x + y ≤ 15 ………………………………………………3        x ≥ 0 , y ≥ 0	B1 B1 B1 B1 GRAPH 3 MKS   B1B1B1 10mks
24	(a) 3∫2 (t2 – 2t + 4) dt       [t3/3 – t2 + 4t]3      (27/3 – 9+12) – (8/3 −4 +8)       12 – 4 − 8/3        8 – 8/3       (24−8)            3     16/3 or 5 1/3  (b) t2 – 4t + 4 = 0       t = 4 ± √(16−4(4)                     2            4 ± 0 = 2               2  (c) a = dv/dt          = 2t – t (at t = 2)        a = 2(2) – 2         a= 2 m/s2	M 1 M1   M1     A1 M1   M1 A1   M1 M1 A1