Mathematics Form 1 Questions and Answers - End Term 2 Exams 2021

Share via Whatsapp
English Form 1 Questions and Answers - End Term 2 Exams 2021 - Next »
Download PDF for future reference Get on Whatsapp for 50/-

Mathematics Form 1 End Term 2 Exams 2021 with Marking Schemes

  1. Write in words 437 308 041. (2mks)
  2. Test whether the number 24831 is divisible by 3. (3mks)
  3. Three tanks are capable of holding 361, 841 and 901 of milk. Determine the capacity of the greatest vessel which can be used to fill each one of them on exact number of times. (3mks)
  4. Write the following in standard form. (2mks)
    1. 0.001576
    2. 325.87
  5. Use tables to find the:
    1. Square of 36.21 (2mks)
    2. Square root of 0.0293 (2mks)
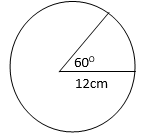
  6. Find the perimeter of the figure below. (3mks)
    math6
  7. If x = -2, y =-6 and z=4, find the value of: (2mks)
    3YZ
      X
  8. Express the following numbers as a product of prime factors.
    1. 472 (2mks)
    2. 1078 (2mks)
  9. Arrange the following fractions in ascending order. (2mks)
    11/12, 5/6, 2/3, 5/6
  10. The sum of three consecutive whole numbers is 84. Find the numbers. (3mks)
  11. Express the following as a fraction.
    0.67˙ (3mks)
    2.8˙3˙ (3mks)
  12. Maureen spent sh. 207 to buy 7 exercise books and 4 pens while Sharon spent sh. 165 to buy 5 exercise books and 5 pens of same type. Find the cost of each item. (3mks)
  13. The sum of interior angles of a regular polygon is 720O. Find the number of sides of the polygon and give its name. (3mks)
  14. A lady bought US £ 5000. From this, she spent US£ 1000 on a return ticket and US£ 1750 while in USA. Upon her return, she sold the remaining dollars. Using the following exchange rate:
    Currency buying selling
    1US Dollar (£) 78.4133 78.4744

    1. How much did she pay to the bank in Kenya shillings to yet the US £ 5000? (2mks)
    2. How much in Kenya shilling did she get after selling the remaining amount to the bank? (2mks)
  15. Solve the following pair of simultaneous equations graphically. (6mks)
    2x – y = 3
    X + 2y = 14


SECTION II (20MKS)
Answer all questions.

  1. The travel timetable below shows the departure and arrival times for a bus plying between two towns M and R, 300km apart.
    Town  Arrival  Departure 
    M   0830h
    N 1000h 1020h
    P 1310h 1340h
    Q 1510h 1520h
    R 1600h  

    1. How long does the bus take to travel from town M to N? (2mks)
    2. What time does it take at town P? (2mks)
    3. At what time does it arrive at town R in 12hr clock system? (2mks)
    4. What is its average speed for the whole journey? (4mks)

  2. Daniela spent ¼ of her net January salary on school fees. She spent ¼ of the remainder on electricity and water bills. She then spent 1/9 of what was left on transport. If she finally had sh. 3400.
    1. What fraction of her January salary was spent on electricity and water bill? (2mks)
    2. What fraction remained after she spent on fees, electricity and water bills? (2mks)
    3. What fraction was spent on transport? (2mks)
    4. Calculate her net January salary. (4mks)

Marking Scheme

 

  1. Write in words 437 308 041.   (2mks)
    Four hundred and thirty seven million three hundred and eight thousand and fourty one.
  2. Test whether the number 24831 is divisible by 3.           (3mks)
    24831
    2+4+8+3+1= 18/3 = 6 it is divisible by 3
  3. Three tanks are capable of holding 361, 841 and 901 of milk. Determine the capacity of the greatest vessel which can be used to fill each one of them on exact number of times.                     (3mks)
    2  36 84 90
    3 18 42 45
      6 14 15
  4.  Write the following in standard form.           (2mks)
    1. 001576
      1.576 x 10-3
    2. 325.87
      3.2587 x 102
  5. Use tables to find the:
    1. Square of 36.21                     (2mks)
      36.212 = (3.621 x 101)2
       3.6212 x 102
      13.111 x 102 = 1311.1
    2. Square root of 0.0293    (2mks)
      0.0293 ½ = (2.93 x 10-2) ½
                       2.93 ½ x 10-1
                       1.7117 x 10-1
                       0.17117
  6. Find the perimeter of the figure below.                     (3mks)
    300/360 x 2 x 22/7 x 12 = 62.8571
    Perimeter = 62.8571 + 12 + 12 = 86.8571 cm
  7. If x = -2, y =-6 and z=4, find the value of:           (2mks)
    3YZ
       X
    3YZ = 3X – 6 X 4 = -72 = 36
       X              -2           -2
  8. Express the following numbers as a product of prime factors.
    1. 472           (2mks)
      2[472
      2[236
      2[118
       [59
      472 = 23 x 59
    2.  1078                     (2mks)
      2[1078
      7[539
      7[77
      1[11
      1078= 2 X 72 x 11
  9. Arrange the following fractions in ascending order.           (2mks)
    11/12, 5/6, 2/3, 5/6
    11/12 x 2, 5/6 x12, 2/3 x 12, 5/6 x 12
    11, 10, 8,10
    Ascending order: 2/3,5/6,5/6,11/12
  10. The sum of three consecutive whole numbers is 84. Find the numbers.     (3mks)
    x + x + 1 + x + 2 = 84
    3x + 3 = 84
    3x /3 = 81/3
    X= 27, the numbers are : 27, 28 and 29
  11. Express the following as a fraction.
    1. 0.67˙           (3mks)
      Let r = 0.6777
      10r = 6.777
      100r = 67.777
      100r – 10r = 67.777 – 6.777
      90r = 61/90
      90r
      r = 61/90
    2. 2.8˙3˙           (3mks)
      Let r = 2.838383
           10r = 28.383838
           100r = 283.838383
      100r – r = 283.838383 – 2.838383
      99/99r = 281/99
      R= 281/99 or 2 83/99
  12. Maureen spent sh. 207 to buy 7 exercise books and 4 pens while Sharon spent sh. 165 to buy 5 exercise books and 5 pens of same type. Find the cost of each item.   (3mks)
    7e + 4p = 207 …. X 5
    5e + 5p = 165 …. X 4
    35e + 20p = 1035
    20e + 20p = 660
    15/15e            375/15
    e = 25
    7 (25) + 4p = 207
    175 + 4p = 207
    4/4p = 32/4
    P = 8
    The cost of 1 exercise book = shs. 25 and the cost of a pen sh. 8.
  13. The sum of interior angles of a regular polygon is 720O. Find the number of sides of the polygon and give its name. (3mks)
    (22n – 4) 90 = 720/90
            90
    2n – 4 = 8
    2/2n = 12/2
    n = 6
    number of sides = 6. hexagon
  14. A lady bought US £ 5000. From this, she spent US£ 1000 on a return ticket and US£ 1750 while in USA. Upon her return, she sold the remaining dollars. Using the following exchange rate:
    Currency                        buying                            selling
    1US Dollar (£)                78.4133                          78.4744
    1. How much did she pay to the bank in Kenya shillings to yet the US 5000?   (2mks)
      1 US dollar = sh. 78.4744
      5000 dollar = 5000 x 78.4744
                                       1
                         = sh. 392 372
    2. How much in Kenya shilling did she get after selling the remaining amount to the bank?         (2mks)
      5000 – 1000 – 1750 = 2250 dollars
      1 US dollar = sh. 78.4133
      2250 dollars = 2250 x 78.4133
                                        1
                         = sh. 176 429.90
  1. Solve the following pair of simultaneous equations graphically. (6mks)
    2x – y = 3
    2x – y = 3
    x       0   3
    y     -3   3

    X + 2y = 14
    x + 2y = 14
    x     0   4
    y     7   5

SECTION II (20MKS)

Answer all questions.

  1. The travel timetable below shows the departure and arrival times for a bus plying between two towns M and R, 300km apart.
    1. How long does the bus take to travel from town M to N? (2mks)
      1000
      0830
      130                  = 1hr 30mins
    2. What time does it take at town P? (2mks)
      1340
      1310
           30               = 30 mins
    3. At what time does it arrive at town R in 12hr clock system? (2mks)
      1600
      1200
      400                = 4.00 pm
    4. What is its average speed for the whole journey? (4mks)
      1600
      0830
      7 30               = 7 ½ hrs or 15/2 hrs
      Average speed = total distance covered
                                 Total time taken
                              = 300/15/2
                              = 40km/h
  2. Daniela spent ¼ of her net January salary on school fees. She spent ¼ of the remainder on electricity and water bills. She then spent 1/9 of what was left on transport. If she finally had sh. 3400.
    1. What fraction of her January salary was spent on electricity and water bill?   (2mks)
      ¼ x ¾ = 3/16
    2. What fraction remained after she spent on fees, electricity and water bills?    (2mks)
      ¼ + 3/16 = 7/16
      Remaining = 16/16 – 7/16 = 9/16
    3. What fraction was spent on transport? (2mks)
      1/9 x 9/16 = 1/16
    4. Calculate her net January salary. (4mks)
      7/16 + 1 /16 = ½
      ½    -->   3400
      1     -->    1 x 3400
                           ½
                          = sh. 6800

Download Mathematics Form 1 Questions and Answers - End Term 2 Exams 2021.


Tap Here to Download for 50/-



Join our whatsapp group for latest updates
Read 4758 times Last modified on Tuesday, 09 February 2021 07:35
English Form 1 Questions and Answers - End Term 2 Exams 2021 - Next »
Print PDF for future reference
Published in Form 1 End Term 2 Exams 2021 with Answers
Tagged under

Related items

back to top