Mathematics Paper 1 Questions and Answers - Form 4 End Term 1 Exams 2022

Share via Whatsapp

Next Topic »
Mathematics Paper 2 Questions and Answers - Form 4 End Term 1 Exams 2022

Download PDF for future reference Get on Whatsapp for 50/-

Questions

INSTRUCTIONS TO CANDIDATES

Write your name and Index number in the spaces above.
Sign and write the date of the examination in the spaces provided above.
This paper contains two sections. Section I and II.
Answer all questions in section I and ONLY five in section II.
All answers and working must be written on the question paper in the spaces provided below each question.
Show all the steps in your calculations giving your answer at each stage in the spaces provided below each question.
Marks may be awarded for correct working even if the answer is wrong.
Non-programmable silent calculators may be used and KNEC Mathematical tables may be used, ex- cept where stated otherwise.

Section I

Evaluate: (3marks)
(1 ³/₇ - ⁵/₈) × ²/₃
¾ + 1⁵/₇ ÷ ⁴₇ of 2 ¹/₃
A line passing through points P (4, a) and Q (3, 2) is perpendicular to the line 3y + x + 3 = 0. Find the value of a and write down equation of line PQ. (4 marks)
Use reciprocal tables to find the value of (0.325)^-1 hence evaluate (^{3√0.0000125}/_0.325 ), give answer to 4 s.f. (3marks)
Solve for x in the equation (3marks)
x-3 - x+3 = x
4 6 3
Using the three quadratic identities only factorize and simplify: (4marks)
(x-y)² -(x+y)²
(x²+y²)² - (x²-y²)²
In a regular polygon, the exterior angle is ¹/₃ of its supplement. Find the number of sides of this polygon. (3marks)
Find the area of a segment of a circle whose arc subtends an angle of 22¹/₂ on the circumference of a circle, radius 10cm. (3marks)
Mr. Onyangos piece of land is in a form of triangle whose dimensions are 1200m, 1800m and 1500m respectively. Find the area of this land in ha.(give your answer to the nearest whole number) (3marks)
Two men each working for 8hours a day can cultivate an acre of land in 4 days. How long would 6men, each working 4hours a day take to cultivate 4 acres? (3marks)
From a viewing tower 30metres above the ground, the angle of depression of an object on the ground is 30⁰ and the angle of elevation of an aircraft vertically above the object is 42⁰.Calculate the height of the aircraft above the ground. (3marks)
Solve the following inequality and show your solution on a number line. (3marks)
4x – 3 ≤ ½ (x + 8) < x + 5
Using a ruler, a pair of compasses only and (proportional) a set square, construct on the upper side division of line BC is 6cm, a line BD such that DBC = 37.5^o. Use the line BD to divide BC into 4 equal portions. (3marks)
A Kenyan bank buys and sells foreign currency as shown below.

Buying Ksh Selling Ksh

1 US dollar ($) 103.00 106.20

1 UK pound (£) 145.00 149.95

A tourist arrived in Kenya with £9600 which he converted into Kshs at a commission of 5%. He later used ¾ of the money before changing the balance of dollars at no commission calculate; to the nearest dollar, the amount he received. (3marks)
A map is drawn to scale of 1:50,000. Find the area in cm2 on the map of a field with an actual area of 60,000m2. (3marks).
Two similar solids have surface areas of 48cm2 and 108cm2 respectively. Find the volume of the smaller solid if the bigger one has a volume of 162cm3. (3marks).
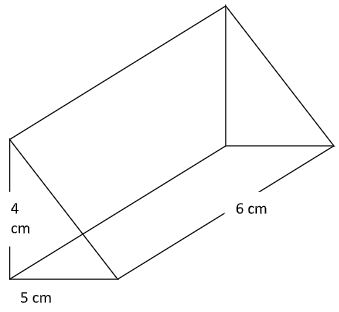
The diagram below represents a prism whose cross section is a right angled triangle. Draw a labeled sketch of the net of the prism. (3marks).

Section II. Answer any five questions.

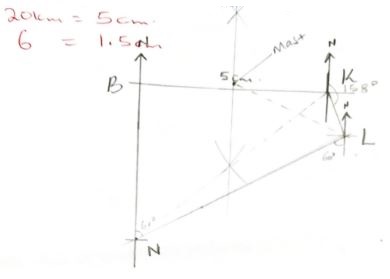
Four schools: Lihanda, Kagito, Bar-Sari and Ndori are such that Lihanda is 6km from Kagilo on a bearing of 158°, Bar-Sauri is to the west of Kagilo and 20km away while Ndori is to the South of Bar-sauri on a bearing of 240° from Lihanda.
1. Using a scale of 1:400,000 draw a scale diagram showing the relative positions of the four schools (5mark)
2. Using your diagram determine the distance and bearing of Ndori from Kagilo. (2 marks)
3. A mast is to be erected so that it is equidistant from Kagilo and Bar-sauri and 20km from Ndori. On the same diagram show the position of the mast and find its distance from Lihanda. (3marks)
A commemorative stone is sculptured in a shape of a frustum of a cone with the diameters of the top and bottom faces being 28cm and 49cm respectively. If the vertical distance between the faces is 45cm, find:
1. Find the cones vertical height. (2marks)
2. Find the volume of the stone. (3 marks)
3. Surface area of the stone. (5 marks)
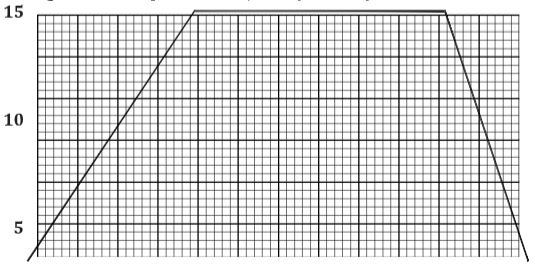
The graph in figure below represents the journey made by a matatu between two bus stops.
1. What is the acceleration of the matatu? (2 marks)
2. Calculate the deceleration of the matatu? (2 marks)
3. What distance does the matatu cover while accelerating? (2 marks)
4. Calculate the distance covered by matatu while decelerating (2marks)
5. Calculate the distance between the two bus stops. (2 marks
An amount of money was shared among five boys Ali, Juma, Musa, Khalid and Mustafa. Ali got 3/8 of the total amount while Juma got 2/5 of the remainder. The remaining amount was shared equally among Musa, Khalid and Mustafa, each of which received Kshs 600.
1. How much did Juma get? (3 marks)
2. How much was shared among the five boys. (2 marks)
3. Ali, Juma and Mustafa invested their money and earned a profit of Kshs 1200. A third of the profit was left to maintain the business and the rest shared according to their investments. Calculate how much each got. (5 marks)
In the diagram below, two circles centres A and C have radii 70cm and 102cm respectively, intersects at B and D . BD = 96cm
1. Find the length AC (3 marks)
2. Calculate
  1. Angle BAD (2 marks)
  2. Angle BCD (2 marks)
  3. The area of the shaded part. (3 marks)
A particle P moves in a straight line such that t seconds after passing a fixed point Q. its velocity is given by the equation
2t² -10t + 12 find:
1. The values of t when p is instantaneously at rest. (2 marks)
2. An expression for the distance moved by P after t seconds. (2 marks)
3. The total distance traveled by P in the first 3 seconds after passing point O. (3 marks)
4. The maximum velocity attained by the body. (3 marks)
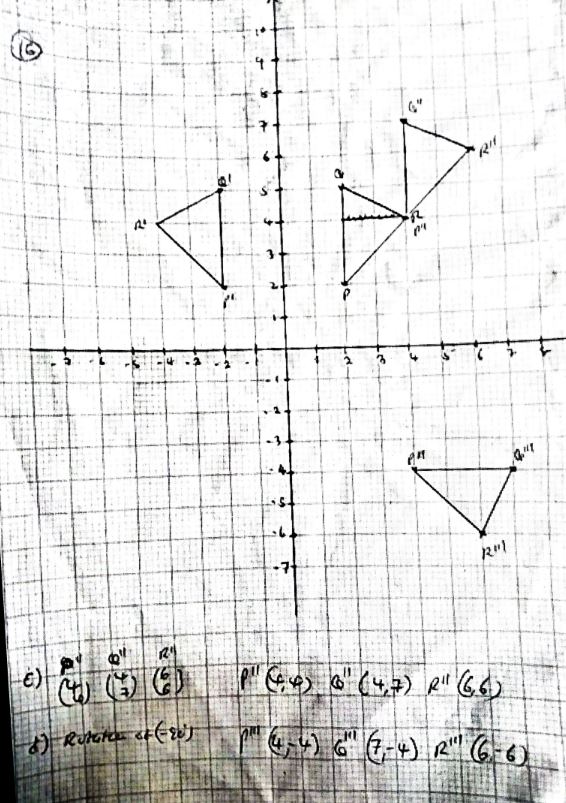
On the graph paper provided plot the points P(2,2) Q(2,5) and R(4,4)
1. Join them to form a triangle PQR (1mk)
2. Reflect the triangle PQR in the line x=0 and label the image s P1Q1R1. (2mks)
3. Triangle PQR is given translation by vector T () to P11Q11R11.plot the triangle P11Q11R11. (3mks)
4. Rotate triangle P11Q11R11 about the origin through -900.state the coordinates of P111Q111R111. (3mks)
5. Identify two pairs of triangle that are direct congruence (1mk)
A bus and a matatu left voi for Mombasa 240km away at 8:00 am travelled at 90km/h and 120km/h respectively. After 20 minutes the matatu had a puncture which took 30 minutes to mend. It then continued with the journey.
1. How far from voi did the matatu catch up with the bus(6 mks)
2. At what time did the matatu catch up with the bus?(2mks)
3. At what time did the bus reach Mombasa?(2mks)

Marking Scheme

Numerator
10/7 - 5/8 = 45/56
45/56 x 2/3 = 15/28

Denominator
4/7 x 7/3 = 4/3
12/7 ÷ 4/3 = 12/7 x 3/4 = 9/7
3/4 + 9/7 = 57/28
15/28 ÷ 57/28=
15/28 x 28/57 = 15/57
5/19
3y = -x-3
y= -1/3x -1
m1m2 = -1
m2 = -1x-3
3= a-2/4-3
3= a-2
a=5
3 = 5-y/4-x
12-3x= 5-y
y= 3x + 5 -12
y= 3x -7
0.325^-1=
1/ 3.25 x 102 = 3.0769
³√0.0000125
=(12.5 x 10^-6)^¹/₃ = 5/100
= 3.0769 x 5/100 = 0.1538
3x -9 -2x -6 = 4x
x-15 = 4x
3x=-15
x=-5
(x-y)² = (x+y)(x-y)
x² - 2xy + y² - x² - 2xy - y²
Num - -4xy
Denom - x² + 2x²y² + y⁴ - x² + 2x²y² + y⁴ = 4x²y²
- 4xy/ 4x²y² = ^-1/_xy
1/3 + x = 180
4/3x = 180
x = 180 x 3/4= 135
exterior= 135 x 1/3 = 45
n= 360/45
8 sides
^θ/₃₆₀ πr²
^22.5/₃₆₀ x ²²/₇ x 10²
= 19.63cm²
√s(s-a)(s-b)(s-c)
s= 1500 + 1800 +1200
2
s= 2250
A=√2250(2250-1500)(2250-1200)(2250-1800)
=√2250.750.450.1050
= 892941.3675m2
(892941.20/10,000)ha
= 9ha
m hrs A Days
2 8 1 4
4 4
= (2 x 8 x 1 x 4)4
6 x 4
= 10.6 days
= 11 days
x = 30 = 51.96
Tan 30°
y = 51.96 x tan42 = 46.79
= 79.79
4x - 3 < 1/2(x+ 8)
3 1/2x > 7
x < 2
1/2x + 4 < x + 5
-1 < 1/2x
-2 < x
-2 < x < 2
95/100 x 9600 x 145 = 1,322,400
money left = 1-3/4 = 1/4
1/4 x 1,322,400 = 330, 600
into $ = 330,600 = $3112.99
106.20
= $3113
12cm = (50,000 x 50,000)
100 100
= 250,000
60,000 = 0.24cm²
250,000
L.S.F = √48/108 = ³√x/162
= (²/₃)³ = ^x/₁₆₂x = (²/₃)³ x 162
= 48cm³
2. N.K = 7.8cm ± 0.1cm = 4000cm = 4km
  = 7.8 x 4
  = 31.2 km
3. 3.9cm ± 0.1
  3.9 x 4
  = 15.6km
1. R = H
  r h
  = 24.5 = 45 + h
  14 h
  24.5h = 14h + 630
  10.5h = 630
  h= 60cm
  H= 60 + 45
  = 105cm
2. 1/3πr²h
  = 1/3π(24.5² x 105 - 14² x 60)
  = 53, 685.89cm³
3. 1/3πrl
  142 + 602 = l2
  l2 = 61.61
  l = 10.5
  61.61 60
  l = 105 x 61.61
  60
  = 107.8
  = 1/3 π (107.8 x 24.5 - 14 x 61.61)= 1862.50
  area c1 = 14 x14 x 22/7 = 615.75
  C2 = 24.52 x 22/7 = 1885.74
  = 4363.99cm2
1. a = 15-0 = 0.75m/s²
  20-0
  = 0.75 m/s2
2. a = 15 - 0
  50 -60
  15 / -10 = -1.5m/s2
3. A = 1/2 x 20 x 15= 150
4. Area = 1/2 x 10 x 15 = 75
5. Area = 1/2h(a+b)
  = 1/2 x 15(60 + 30)
  = 7.5 x 90
  = 675M
1. Ali - 3/8 x
  Juma = 2/5 of (1-3/8)x = 1/4x
  Remaining = (1 - (3/8 + 1/4))x = 3/8x
  3/8 x 1/3 = 600
  x = 600 x 8
  = 4800
2. 3/8x = 4800
  x = 4800 x 8
  3
  = 12,800
3. Ali = 3/8 x 12,800 = 4,800
  Juma = 1/4 x 12, 800 = 3200
  Mustafa = 600
  8600
  Ali = 4800   x 1200 = 670
  8600
  Juma = 3200   x 1200 = 446.50
  8600
  Mustafa = 600   x 1200
  8600
  = 84
1. Ax² = 70² - 48²
  Ax = 50.95
  Cx² = 102² - 48²
  Cx = 90
  AC = Ax + Cx = 90 + 50.95 = 140.95cm
2. 1. <BAD = 2<BAX
    Sin <BAX = 48/70
    <BAX = Sin-1 (48/70)
    = 43.29°
    <BCD = 56.14°
1. V = 2t² - 10t + 12
  ²/₂t² - ^10t/₂ +¹²/₂ = 0
  t² - 5t + 6=0
  t=3 or t=2
2. ds/dt = 2t² - 10t + 12
  s= ∫2t³ - 10t + 12dt = 2/5t³ - 5t² + 12t + c
3. ∫_₀^³2t² - 10t + 12dt
  = 2/3t³ - 5t² + 12t
  = 2/3(3)³ - 5(3)² + 12(3)
  18-45 + 36
4. a = dv/dt = 4t -10
  4t - 10 = 0
  s= 2.5s
  V = 2 x 2.52 - 10 x 2.5 + 12 = 0.5m/s2
1. D= S xT
  20 x 20/60
  = 40km
  D= S xT
  90 x 50/60
  = 75km
  RD = 35km
  R. Speed
  (120 - 90)= 30 km/hr
  R.T = ³⁵/₃₀ = 1¹/₆hr
  =⁷/₆hrs
  D= SxT
  = 120 x⁷/₆= 140km
  D from voi = 40 + 140 = 180km
2. (8.00am + 20 mins + 30 mins)
  8:50 + 1 hrs 10 mins
  = 10.00 am
3. T= D/S
  240/90 = 2 2/3hrs or 8/3hrs
  8:00 am + 2hrs 40 mins
  10:40am