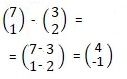Mathematics Paper 2 Questions and Answers - Form 4 End Term 1 Exams 2022

Questions

INSTRUCTIONS TO CANDIDATES

1. Write your name and Index number in the spaces above.
2. Sign and write the date of the examination in the spaces provided above.
3. This paper contains two sections. Section I and II.
4. Answer all questions in section I and ONLY five in section II.
5. All answers and working must be written on the question paper in the spaces provided below each question.
6. Show all the steps in your calculations giving your answer at each stage in the spaces provided below each question.
7.  Marks may be awarded for correct working even if the answer is wrong.
8. Non-programmable silent calculators may be used and KNEC Mathematical tables may be used, ex- cept where stated otherwise.

SECTION I ( 50 MARKS)

1. Use logarithm table to evaluate (4mks)
   
2. Three sisters, Ann, Beatrice and Caroline together harvested Ksh 48,000 as capital & started as small business. If the share of profit is Kshs 2,300, Kshs 1,700 & Kshs 800 respectively, share proportionally.
   Find the capital invested by each of them; (3mks)
3. Make t the subject of the formula in (3mks)
   x( ^{p + t}/_t) 1/3
4. Simplify the expression (3mks)
   3x² – 4xy + y²
      9x² – y²
5. A (-6, -2) and B (2, -4) are end points of a diameter of a circle. Find the co-ordinates of the center and the radius of the circle. (3mks)
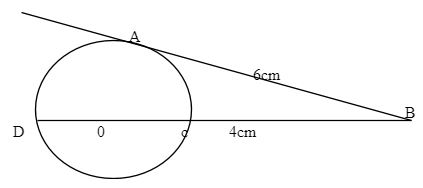
6. In the figure below AB is a tangent to the circle and BCD is a straight line passing through the center of the circle. AB =6cm and BC= 4cm. Calculate the radius of the circle. (3mks)
   
7. Solve the equation below in the range 00x 1800 25 in (3x + 10) = -1.674 (3mks)
8. Expand and simplify (3x - y)4 hence use the first three terms of the expansion to approximate the value of (6 – 0.2)4 (3mks)
9. Find x without using table if (3mks)
   3 + log ₂2 + log₂x = log ₂5 + 2
10. Without using mathematical table or calculator simplify (3mks)
      3√2 - √ 3  
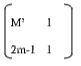
    2√3 - √2
11. Find the value of m for which the matrix transforms an object into a straight line (3mks)
    
12. A right angled triangle has a base of 15.3cm and height 7.2cm, each measured to the nearest 3mm. Determine the percentage error in finding the area of the triangle giving your answer to 2 dp (4kms)
13. The point B(3,2) maps onto B (7,1) under a transformation T1. Find T1 (2mks)
14. Solve for x 8 y in the simultaneous equation using matrices method. (4mks)
    2x + 3y = 7
    y – x = 2
15. The sum of the first ten terms of an arithmetic progression in 400. If the sum of the first 6 terms of the same series is 120, find the 15th term. (3mks)
16. Two grade of tea A & B, costing sh100 and 150 per kg respectively are mixed in the ratio 3.5 by mass. The mixture is then sold at sh 160 per kg. Find the percentage profit on the cost price. (3mks)

SECTION B
Attempt five questions in this section.

17. The frequency distribution table below represents the number of kilograms of meat sold in a butchery
    

    Mass in kg	1-15	6-10	11-15	16-20	21-25	26-30	31-35
    Frequency	2	3	6	8	3	2	1

    Export graph
    1. State the modal frequency (1mk)
    2. Calculate the mean mass using assumed mean of 18kg (5mks)
    3. Calculate the median mass (4mks)
18. A plane leaves an airport A(41.50 N, 36.40W) at 9.00AM and flies due north to Airport B on latitude 53. 20. Taking ∏ as 227 and the radius of the earth as 6370km.
    1. Calculate the distance covered by the plane in km (4mks)
    2. The plane stopped for 30minutes to refuel at b and flew east to C 2500km from B. Calculate
       1. Position of C (3mks)
       2. The time the plane land at C if its speed is 500km/h
19.             
    1. Draw a rectangle ABCD of legth AB = 7.5cm and width 4.8cm and construct the locus of point P with the rectangle such that P is equidistant from BC & CD (4mks)
    2. If the locus of P meets AB at N, measure AN (1mk)
    3. Construct the locus of point Q with the rectangle and in the same side as D such that angle NQC = 600 (3mks)
    4. Determine the area of the trapezium (2mks)
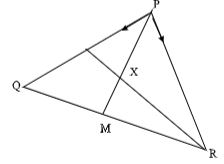
20. In the triangle PQR below L & M are points of PQ & QR respectively such that PL:LQ = 1:3 and QM :MR = 1:2. PM & PL intersect at X. Given that PQ = b and PR = c
    
    
    1. Express the following vectors in terms of b & c
       1. QR (1mk)
       2. PM (1mk)
       3. RL (1mk)
    2. By taking PX = KPM and RX = hRL where K and h are constants. Find two expressions for PX in terms of K, b, h and c. Hence determine the values of the constants k and h (6mks)
    3. Determine the ratio LX:XR (1mk)
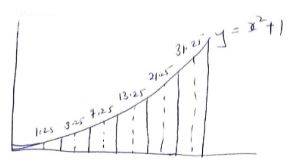
21. The curve given by the equation y = x2 +1 is defined by the values in the table below.
    1. Complete the table by filling in the missing values.
       

       X	0	0.5	1.0	1.5	2.0	2.5	3.0	3.5	4.0	4.5	5.0	5.5	6.0
       Y	1.0		2.0		5.0		10.0		17.0		26.0		37.0

    2. Sketch the curve for y = x2 + 1 for 0 ≤ x ≤ 6
    3. Use the mid-ordinate rule with 5 ordinates to the area of the region bounded by the curve y = x2 + 1, the axis the lines x = 0 and x = 6 (2mk)
    4. Use method of integration to find the exact value of the area of the region in (C) above. (2mk
    5. Calculate the percentage eror involved in using the mid- ordinate rule to find the area. (2mk)
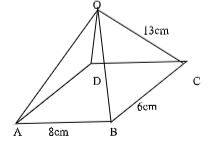
22. OABCD is a right pyramid on a rectangular base with AB = 8cm, BC = 6cm, OA = OB = OC = OD =13cm. Calculate:
    
    
    1. The height of the pyramid
    2. The inclination of OBC to the horizontal (2mks)
    3. The angle between
       1. OB & DC
       2. The planes OBC & OAD
23. A particle moves such that t seconds after passing a given point O, its distance 5 metres from O is given as 5 = t (t-2)(t-1)
    1. Find its velocity where t = 2 seconds (3mks)
    2. Find its minimum velocity (2mks)
    3. Find the time when the particle is momentarily at rest (3mks)
    4. Find the acceleration when t = 3 seconds (3mks)
24. The headmaster wishes to hire two matatus for a trip. The operators have a Toyota which carries 10 passengers and a Kombi which carries 20 passengers. Altogether 120 people have to travel. The operators have only 20 litres of fuel and the Toyota consumes 4 litres on each round trip and the Kombi 1 litre on each round trip. If the Toyota makes x round trips and the Kombi y round trips:
    1. Write down four inequalities in x & y which must be satisfied (2mks)
    2. Represent the inequalities graphically on the grid provided (3mks)
    3. The operators charge shs 100 for each round trip in the Toyota and shs 300 for round trip in the kombi
       1. Determine the number of trips made by each vehicle so as to make total cost 9 minimum (4mks)
       2. Find the minimum cost (1mk)

Marking Scheme

1. 
   

   No	STD Form	Log Table
   27 0.0293	2.7 x 101 2.93 x 10-2	1.4314 2.4669 1.8783           2
   731 0.2861	7.31 x 102 2.861 x 10-1	2.9639 1.4566 4.2893 x 1/4

2. Ann : Beatrice : Caroline
     23      17              8
   23 :17 :8
   48  48  48
   Ann : 23/48 x 48000 = 23000
   Beatrice: 17/48 x 48000= 17000
   Caroline 8/48 x 48000= 8000
   
   
3. (x)³ = ((^p+t/_t)^¹/₃)³
   x³ = ^p+t/_t
   
   x³t= p+t
   x³t-t=p
   t(x³-1) =    p   
   (x³-1)      x³-1
   t= ^P/_x³-1
                
4. 3x²  - 3xy - xy + y²
     (3x+y)(3x-y)
   3x(x-y)-y(x-y)
   (3x+y)(3x-y)
    x+y 
   3x+y
   
   
5. (-6 + 2     -2-4)
       2            2
   Centre(-2, -3)
   
   
   
6. (x+4)4 = 36
   4x=20
   x=5
   radius = 2.5cm
   
   
7. Sin (3x+10)= 0.837
   Sin 0.837 = 56.82
   3x+10 = 236.82, 303.18
   r= 75.61 , 97.93°
   
   
8. 81x⁴ + 108x³y + 54x²y² - 12xy³ + y⁴ 
   3x=6, x=2
   -y=-0.2 , y= 0.2|
   81(2)⁴ + 108(2)³(0.2) + 54(2)²(0.2)² 
   = 324 - 172.8 + 8.64 = 159.84
   
   
9. 3(Log ₂2 )+ Log ₂3 + Log₂x = Log ₂5 + 2(Log ₂2)
   Log ₂8 + Log₂3 + Log₂x = Log ₂5+ Log ₂4
   Log ₂(8 x 3 x x)= Log ₂(5 x 4)
   24x = 20 
   x = 5/6
   
   
10.   √2 - √3    x  2√3 + √2  
    2√3 - √2         2√3 + √2
    3√2(2√3 + √2) - √3(2√3 + √2)
                           10
    6√6 + 6 - 6 - √6
           10
    ¹/₂√6
    
    
11. (m² x 1) - (2m -1)1 = 0
    m² - (2m -1)=0
    m² - 2m + 1= 0
    m(m-1)-1(m-1)=0
    m-1=0
    
    
12. Actual area = 15.3 x 7.2 = 110.16
    Max area = 15.35 x 7.25 = 113.5575
    Min Area = 15.15 x 7.05 = 106.8075
    106.8075 - 113.5573   =  6.75
                 2                           2
    = 3.375
     3.375   x 100
      110.16
    = 2.06
    
    
13. T1 = T' -T
    
14.   
    
    
    
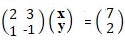
15. S₁₀ = ⁿ/₂ (2a + (n-1)d)
    400 = 5(2a + 9d)
    120 = 3 (2a + 5d)
    
    
16. 3/8(100) + 5/8(150)= cost price
    32.5 + 93.75 = sh 131.25
    profit = 160 - 131.25
    sh = 29.75
    28.75 x 100
      131.25
    = 21.9047619
    = 21.9040%
    
    
17.         
    1. 
       

       Mass in Kg	f	x	d=x-A	fd
       1-5 6-10 11-15 16-20 21-25 26-30 31-35	2 3 6 8 3 2 1	3 8 13 18 23 25 33	-15 -10 -5 0 5 16 15	-30 -30 -30 0 15 20 15

    2. _
       x = A + Σfd = 18 + ^-40/₂₅
                 Σf
       = 16.4
       
       
    3. M = L + (n/2 - c)
                         f
       15.5 + (25/2 - 11)
                        8
       15.5 + (^1.5/₈)5
       15.5 + ¹⁵/₁₆ = 16.4375
       
       
18.                 
    1. distance = ^11.7/₃₆₀ x 2 x ²²/₇ x 6370 = 1301.3km    
    2.            
       1. θ/360 x 2 x22/7 x 6370 Cos52.2 = 2500
          66.6247  =     2500     = 37.53°
           66.6247     66.6247
          
          
       2. t= d/s  1301.3 + 2500
                       500         500
          (2hrs 36min) + 5hrs
          7hrs 36min
          37.52 x 4 = 150.0 = 2hrs
          09:00hrs
          0236     
          1136hrs
          
          1636
            230
          1906
          
          0900h
          0736     
          1636hrs
          7.06
          
          
19.                     
    1. Angle bisector loci
       
       
    2. 2.7cm ± 0.1
       
       
    3. Constant angle loci
       
       
    4. 1/2x(2.7 + 7.5)48 = 24.48cm²
       
       
20.                 
    1.      
       1. QR - c - b
       2. ¹/₃c + ²/₅ b
          
          
    2. PX = ¹/₄hb + 1 - hc
       PX= K(²/₃b + ¹/₃c)
       = ²/₃kb + ¹/₃kc
       ²/₃= ¹/₄h → 8k - 3h =0
       ¹/₃k= 1-h →k + 3h =3
       ak=3
       k=¹/₃
       3h = ⁸/₃
       h=⁸/₉
       
       
    3. 1:8
       
       
21.                
    1.    
       

       X	0	0.5	1.0	1.5	2.0	2.5	3.0	3.5	4.0	4.5	5.0	5.5	6.0
       Y	1.0	1.25	2.0	2.25	5.0	7.25	10.0	13.25	17.0	21.25	26.0	31.25	37.0

    2.       
    3.          
       
       A= 1(1.25 + 3.25 + 7.25 + 13.25 + 21.25 + 31.25)
       1(77.6)
       = 77.5 square units
       
       
    4. _₀∫^⁶ (x2 + 1)dx
       [x³/3 + x + c]_₀^⁶ 
       [216/3 + 6 + c] - (0 + c)
       72 + 6 + c -c
       78sqr units
       
       
    5. 77.5 - 78 = 0.5sqr units
       0.5 x 100
       78
       0.64102564102
       = 0.6410%
       
       
22.                        
    1. √13² - 5²
       =√169 - 25
       =√144 = 12cm
       
       
    2. Tan θ= 12/4
       θ= Tan^-1 3= 71.57°
       
       
    3.          
       1. OB & DC = Cos B = 4/13
          Tyhe planes OBC and OAD 
          B= Cos^-1 = 4/13 = 72.08°
          
          
23.                
    1. s=(t² - 2t)(t-1)
       s=t³ - t² - 2t² + 2t
       s= t³ - 3t² + 2t
       ds/dt 
       v=3t² - 6t + 2
       When t= 2 sec
       v=12 - 12 + 2 = 2m/s
       
       
    2. 6t- 6=0
       When t = 
       3(1)2 - 6(i)+ 2
       = -1m/s
       
       
    3. 0=3t² - 6t + 2
       
       
    4. a = dv/dt = 6t-6
       6(3)-6 = 12m/s²
       
       
24.                       
    1. 10x + 20y > 120
       4x + y < 20
       x > 0
       y > 0