Integers - Mathematics Form 1 Notes

• Introduction
  • The Number Line
• Operations on Integers
  • Addition of Integers
  • Subtraction of Integers.
  • Multiplication
  • Division
  • Order of Operations
• Past KCSE Questions on the Topic

Introduction

The Number Line

• Integers are whole numbers, negative whole numbers and zero.
• Integers are always represented on the number line at equal intervals which are equal to one unit.

Operations on Integers

Addition of Integers

• Addition of integers can be represented on a number line .
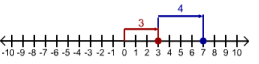
• For example, to add +3 to 0 , we begin at 0 and move 3 units to the right as shown below in red to get +3,
• Also to add + 4 to +3 we move 4 units to the right as shown in blue to get +7.
  
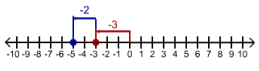
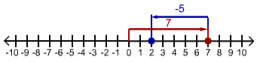
• To add -3 to zero we move 3 units to the left as shown in red below to get -3 while to add -2 to -3 we move 2 steps to the left as shown in blue to get -5.
  
  
  Note;
• When adding positive numbers we move to the right.
• When dealing with negative we move to the left.

Subtraction of Integers.

Example

(+7) – (0) = (+7)

To subtract +7 from 0 ,we find a number n which when added to get 0 we get +7 and in this case n = +7 as shown above in red.

Example

(+2) – (+7) = (-5)

Start at +7 and move to +2. 5 steps will be made towards the left. The answer is therefore -5.

Example

-3 – (+6) = -9

|__|_←|__|__|__|__|__|    |←|__|__|__|__|__|
-4 -3 -2   -1   0   1   2  3    4   5  6   7   8   9   10

We start at +6 and moves to -3. 9 steps to the left, the answer is -9.

Note:

• In general positives signs can be ignored when writing positive numbers i.e. +2 can be written as 2 but negative signs cannot be ignored when writing negative numbers -4 can only be written s -4.
  4 – (+3) = 4 -3
  = 1
  -3- (+6) =3 – 6
  = -3
• Positive integers are also referred to as natural numbers. The result of subtracting the negative of a number is the same as adding that number.
  2 – (- 4) = 2 + 4
  = 6
  (-5) – (- 1 ) = -5 + 2
  = -3
• In mathematics it is assumed that that the number with no sign before it has appositive sign.

Multiplication

- In general

1. (a negative number) x (appositive number ) = (a negative number)
2. (a positive number) x (a negative number ) = (a negative number)
3. (a negative number) x (a negative number ) = (a positive number)

Examples

-6 x 5 = -30
7 x -4 = - 28
-3 x -3 = 9
-2 x -9 = 18

Division

- Division is the inverse of multiplication. In general

1. (a positive number ) ÷ (a positive number ) = (a positive number)
2. (a positive number ) ÷ (a negative number ) = (a negative number)
3. (a negative number ) ÷ (a negative number ) = (a positive number)
4. (a negative number ) ÷ (appositive number ) = (a negative number)

- For multiplication and division of integer:

• Two like signs gives positive sign.
• Two unlike signs gives negative sign
• Multiplication by zero is always zero and division by zero is always zero.

Order of Operations

• BODMAS is always used to show as the order of operations.
  B – Bracket first.
  O – Of is second.
  D – Division is third.
  M – Multiplication is fourth.
  A – Addition is fifth.
  S – Subtraction is considered last.
  
  Example
  6 x 3 – 4 ÷ 2 + 5 + (2-1) =
  
  Solution
  
  Use BODMAS
  
  (2 – 1 ) = 1 we solve brackets first
  (4÷ 2) = 2 we then solve division
  (6 x 3) = 1 8 next is multiplication
  Bring them together
  18 – 2 +5 +1 = 22 we solve addition first and lastly subtraction
  18 + 6 – 2 = 22

Past KCSE Questions on the Topic

1. The sum of two numbers exceeds their product by one. Their difference is equal to their product less five.Find the two numbers. (3mks)
2. 3x – 1 > -4
   2x + 1 ≤ 7
3. Evaluate
   -12 ÷ (-3) x 4 – (-15)
   -5 x 6 ÷ 2 + (-5)
4. Without using a calculator/mathematical tables, evaluate leaving your answer as a simple fraction
   (-4)(-2) + (-12) ÷ (+3) + -20 + (+4) + -6)
              -9 – (15)                  46- (8+2)-3
5. Evaluate -8 ÷ 2 + 12 x 9 – 4 x 6
                           56 ÷7 x 2
6. Evaluate without using mathematical tables or the calculator
   1.9 x 0.032
   20 x 0.0038