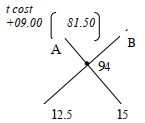Compound Proportions, Mixtures and Rates of Work Questions and Answers - Form 3 Topical Mathematics

Questions

1. Three business partners Georgina, Gilbert and Akumu decided to buy a plot worth shs.510,000. They contributed shs.30000; as a deposit in the ratio 2:3:5 respectively.
   They paid the balance in two months by contributing equal amounts. After one year, they sold the plot for a profit of 20% and invested the initial capital in another business.
   The profit was shared in the ratio 1:2:3; respectively. Find how much each partner
   1. contributed towards the deposit
   2. paid to clear the balance
   3. received as a profit
2. Twelve men take 20 days to complete a piece of work. How long would 16 men take to do the same piece of work?
3. Mr. Kitur bought grades of tea ; Grade A costs shs.109 per kg and a kg of Grade B costs shs.81.50. In what ratio must he mix the two grades in order to make a profit of 20% by selling the mixture at Kshs.112.80per kg?
4. Mogutu and Onacha working together can do a piece of work in 6days. Mogutu working
   alone takes 5days longer than Onacha. How many days does it take Onacha to do the work alone?
5. Given the curve y = 2x3 + ½x2 – 4x + 1, find the equation of the normal to the curve at (1, -½)
6. A and B are connected by the equation B = KA + M where K and M are constants.
   The table below shows the values of A and corresponding values of B
   

   A	1.5	3.0	4.5	6.0	7.5
   B	8	11	14	17	20

   1. Draw a suitable straight line on the grid provided
   2. State the values of K and M, hence express B in terms of A
7. The latitude and longitude of two stations P and Q are (47^oN, 25^oW) and (47^oN, 70^oW) respectively. Calculate the distance in nautical miles between P and Q along the latitude 47^oN
8. A coffee blender mixes 6 parts of types A with 4 parts of type B. If type A costs Kshs. 72 and type B costs him Ksh.66 per kg respectively at what price should he sell the mixture in order to make a profit of 5%. Give your answer to the nearest ten cent.
9. 1. 1. Paint A costs shs.150 per litre while B costs shs.160 per litre. In what proportion must A be mixed with B to produce a mixture costing shs.156 per litre
      2. What must be the selling price of the mixture if a profit of 12% is to be realized?
   2. A cylindrical water tank can be filled to a depth of 2.1m by a pipe P in 2 hours. Pipe Q takes 7 hours to fill the tank to the same level. Pipe R can empty this
      amount of water in 6hours. Initially, the tank is empty. Pipes P and Q are turned on at 8.45a.m and pipe R at 9.45a.m. Find the depth of water in the tank at 11.45a.m
10. Two grades of tea leaves one costing sh.420 per kilogram and the other costing sh. 470 per kilogram are to be mixed in order to produce a blend worth sh.455 per kilogram. In what proportion should they be mixed?
11. The internal radius of a pipe is 0.35m. Water flows through the pipe at the rate of 45cm per second. Calculate the amount of water that passes through the pipe in 2 ¼ hours in litres
12. In 2000 the total cost of manufacturing an item was ksh1250 and this was divided among the costs of material, labour and transport in the ratio of 8:14:13. In 2003 the cost of material
    was doubled, labour cost increased by30% and transport costs increased by 20%
    1. Calculate the cost of manufacturing this item in 2003
    2. In 2004 the cost of manufacturing the same item was ksh1981 as a result of increase in labour costs only. Find the percentage increase in labour costs of 2004
13. Brand A tea costing Kshs.80 per kg is mixed with Brand B tea costing Kshs.100 per kg such that the mixture is sold at Kshs.114 making a profit of 20%. Find the ratio of A:B
14. In what proportion must teas of Kshs.76 and Kshs.84 per kg be mixed to produce a tea costing Kshs.81 per kg
15. Onyango bought 3 brands of tea P, Q and R. the cost price of the three brands were shs.25, shs.30 and shs.45 per kilogram respectively. He mixed the three brands in the
    ratio 5:2:1 respectively After selling the mixture, he made a profit of 20%
    
    1. How much, profit did he make per kilogram of the mixture?
    2. After one year, the cost price each brand was increased by 12%.
       
       1. For how much did he sell one kilogram of the mixture to maintain 20% profit. Give your answers to the nearest 5cts.
       2. What would have been his percentage profit if he sold one kilogram of the mixture at shs.40.25?
16. A mixture contains two powders X and Y with masses in the ratio 3:11. If the mixtures Cost Shs.6.70 per kg and powder x costs Shs.5.60 per kg. Find the cost of 1kg of powder Y

Answers

1. 1. Deposit: Total ratio 2 + 3 + 5 = 10
      Georgina: ²/₁₀ x 30000 = 6000
      Gilbert: ³/₁₀ x 30000 = 9000
      Akumu: ⁵/₁₀ x 30000 = 15000
   2. Balance to be paid
      = 510000 – 30000  = 480000
      Each pays = 480000 = 160000
                             3
   3. Profit = ²⁰/₁₀₀ x 510000 = 102000
      Georgina received: ¹/₆x 102000= 17000
      Gilbert received: ²/₆x 102000 = 34000
      Akumu received: ³/₆ x 102000 = 51000
2. Men    Days
   12        20
   16        ?
   = (12 x 20) days
   16 = 15 days
3.  
   
   Cost of mixture
   Sh 112.8 x 100 = 94 per kg
                    120
   Ratio         A : B
   (81.50 – 94) : (109 – 94)
               12.5 : 15
                 2.5 : 3
                    5 : 6
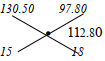
   Alt. At selling Price
   
   A sales at 109 x 120
                           100
   = 130.50/=
   B sales at 81.50 x 120
                              100
   = 97.80/=
   A & B mixed sells at
   94 x 120 = sh 112.80 per kg
       100
   Ratio A : B
   (112.80 – 97.8) : (130 – 112.8)
                       15: 18
                        5 : 6
4. Let Onacha take x days.
   Mogutu takes x + 5 days.
   1   +   1    =  1
   x     x + 5      6 
   x² (x + 5) + 6x = x(x – 5)
   x²–x – 30 = 0
   (x – 10) (x + 3)
   x = 10, 3 Onacha takes 10 days.
5. ^dy/_dx = 6x² + x – 4
   When x = 1,
   ^dy/_dx = 6+1 -4 = 3
   Grad of normal = -¹/₃
   y + ½ = -¹/₃ (x - 1)
   y=-¹/₃ x – ¹/₆
6. Gradient = 11 – 8
                   3 – 1.5
   = 2
   K = 2, M = 5 B = 2A + 5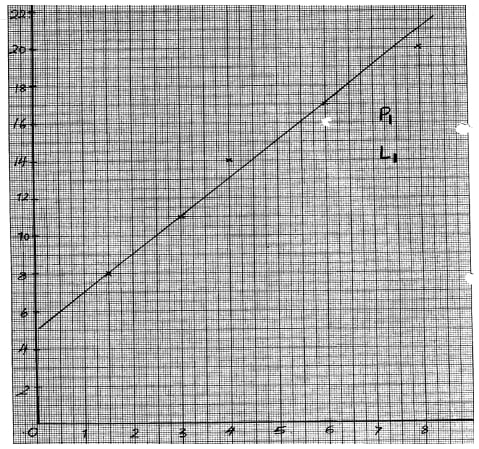
   
   
7. (70 – 25 x 60 = 2700
   2700 Cos 47
   = 2700 x 0.68 = 1841.4nm
8. 6 x 72 + 66 x 4 = 69.6
            10
   100% = 69.6
   ∴ 105 = 73.10
9. 1. 1. A         B     Mixture
         150    160     156
         1          n      1+n
         150    160n   (n+1)156
         
         150 + 160n = 156(n+1)
         N = ⁶/₄ = ³/₂
         = 112 x 156  = shs. 174.72
                 100
   2. At 11.45 a.m
      Depth filled by P in 2hrs = 2.1m
      3hrs = 3hr x 2.1m
                 2hr
      = 3.15m
      Depth filled by q in 7hrs = 2.1m
      3hrs = 3hrs x 2.1m
                 7hrs
      = 0.9m
      Depth emptied by R in 6hrs = 2.1m
      2hrs = 2hr x 2.1
                 6hrs
      ∴ Depth at 11.45a.m = (3.15 + 0.9) – 0.7 = 3.35m
10. Let the amount to be mixed be x kg of the lower, priced grade and y kg for higher price grade
    X kg of the lower priced grade cost Sh. 420x
    Y kg of the higher priced grade cost Sh.470y
    Total cost of (x+y) kg of mixture
    = Shs. 420 x + 470y
                   x + y
    equating 420x + 470y = 455
                     x + y
    420 x + 470y = 455x + 455y
    470y – 455y = 455x – 420y
    15y = 35x
    X: y = 3:7
11. Cross sectional area = r²
    = (22 x 35 x 35)cm²
         7
    Flow per second = (22 x 35 x 35 x 45)cm²
                                 7
    After 2¼ hrs = (22 x 35 x 35 x 45 x 3 x 60 x 69)liters
                            7
    = 233887.5litres
12. 1. In 2000,       Costs              Shs
       Material = 8/25 x 1250 =    400
       Labour = 14/25 x 1250 = 700
       Transport = 3/25 x 1250 = 150
       
       In 2003
       Material = 400 x 2 = 800
       Labour = 130/100 x 700 = 910
       Transport =120/100 x 150 = 180
    2. In 2004 Costs
       Material = 800
       Transport = 180
       ∴ labour = 1981 – (800 + 180)= Shs.1001
       ∴ Increase in labour = 1001 – 910 = 91
       % increase = ⁹¹/₉₁₀ x 100
       = 10%
13. Cost price = 100 x 114 = shs. 95
                           120
    Let A: B = n :1
    95 = 80n + 100
    1          n + 1
    95n + 95 = 80n + 100
    15 n = 5
    n =¹/₃
    n:1 =1:3
    A:B = 1:3
14. Let the ratio be x: y
    76x + 84y = 81(x + y)
    84y – 81y = 81x – 76x
    3y = 5x
    3 = x
    5    y
    x : y = 3 : 5
15. 1. Cost of 8kg = 5 x 25 + 2 x 30 + 1 x 45 = 230
       Cost of 1 kg= 230/8 = 28.75
       Profit/ kg= 28.75 X 20/100
       = 5.75
    2. 1. Selling price
          = 28.75 x ¹¹²/₁₀₀ = 32.20
          32.20 x ¹²⁰/₁₀₀ = 38.64
          38.64
       2. New cost/ kg
          = 1.12 x 28.75 = 32.20
          % Profit = 40.25 – 32.20 X 100
                          32.20
          = 25%
16.  = 3(5.60) + 11y = 6.70
                 14
    = 16.8 + 11y = 93.8
    11y = 77
    y = 7
    1Kg costs Shs. 7.00