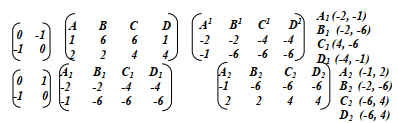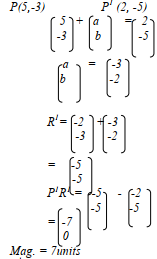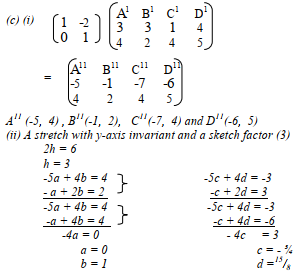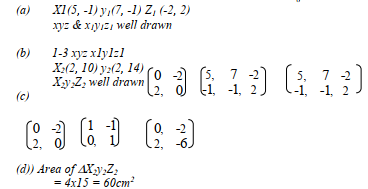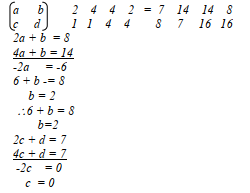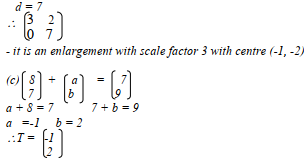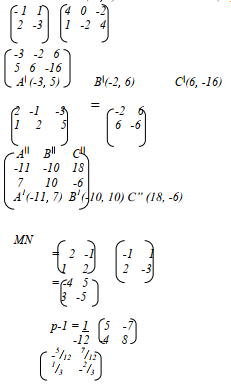Matrices and Transformations Questions and Answers - Form 4 Topical Mathematics

Questions

1. 1. Given triangle ABC with vertices A (-6, 5), B(-4, 1) and C(3, 2) and that A(-6, 5) is mapped onto A¹(-6, -4) by a shear with y-axis in variant. On the grid provided below;
      1. draw triangle ABC
      2. draw triangle A¹B¹C¹, the image of triangle ABC, under the shear
      3. determine the matrix representing the shear
   2. Triangle A¹B¹C¹ is mapped onto A¹¹B¹¹C¹¹ by a transformation defined by the matrix 
      1. Draw triangle A¹¹B¹¹C¹¹ on the same grid as ABC and A¹B¹C¹
      2. Describe fully a single transformation that maps A¹¹B¹¹C¹¹
2.  
   
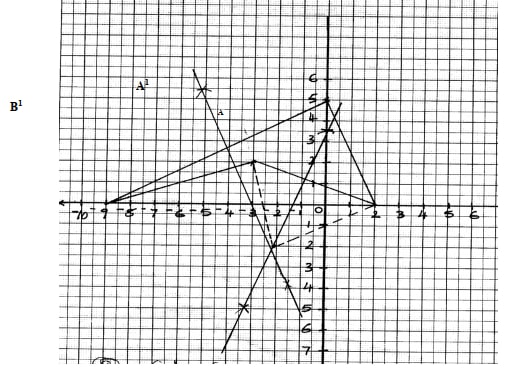
   1. Under a certain rotation A( 2,0) is mapped onto A¹(-4, 2) and B(0,5) is mapped onto B¹(-9, 0)
      1. On the grid provided plot the lines AB and A¹B¹ on the same axes
      2. Hence determine by construction the co-ordinates of the centre and angle of rotation
   2. Under a quarter positive turn about the origin O, A¹ is mapped onto A¹¹ and B1 is mapped onto B¹¹. Determine the co-ordinates of A¹¹ and B¹¹
   3. Describe fully a single transformation which would map A to A¹¹ and B to B¹¹
3. A transformation T is represented by the matrix  and transformation U by  the matrix. Given that a rectangle has co-ordinates at A (1,2) B(6, 2), C(6, 4) and D (1, 4) and that under T the image of ABCD is A¹B¹C¹D¹ and under U the image of A₁B₁C₁D₁ is A₂B₂C₂D₂:
   1. Find the co-ordinates of A₁B₁C₁D₁ and A₂B₂C₂D₂
   2. On the grid provided, plot ABCD, A₁B₁C₁D₁ and A₂B₂C₂D₂
   3. Describe the transformation represented by:-
      1. U
      2.  UT
   4. If A₂B₂C₂D₂ were to be transformed by a transformation represented by the matrix to map onto A₃B₃C₃D₃ . What would be the area of A₃B₃C₃D₃
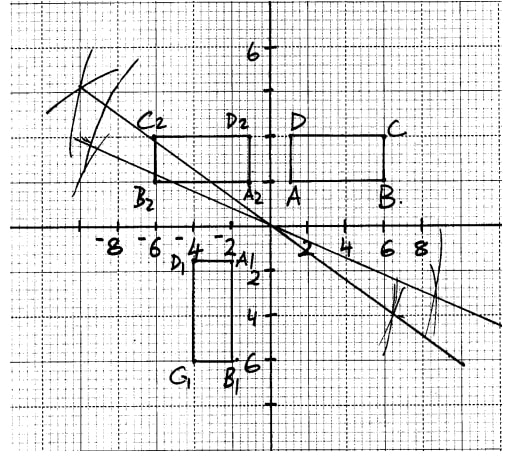
4. The vertices of a quadrilateral are A(2,2) B(8,2), C (8,6) and D(6,4) under a rotation the images of vertices A and D are A(0,8) and D¹(-2, 12).
   1. On the grid provided and using the same axes draw the quadrilateral ABCD and the points A¹ and D¹
   2. Determine the centre and angle of rotation
   3. Locate the points B¹ and C¹ under the rotation and complete the quadrilateral
5. A translation maps the point P(5, -3) onto P¹(2, -5)
   1. Determine the translation vector T
   2. A Point R¹ is the image of R(-2, -3) under the same translation in (a) above, find the magnitude of P¹R¹
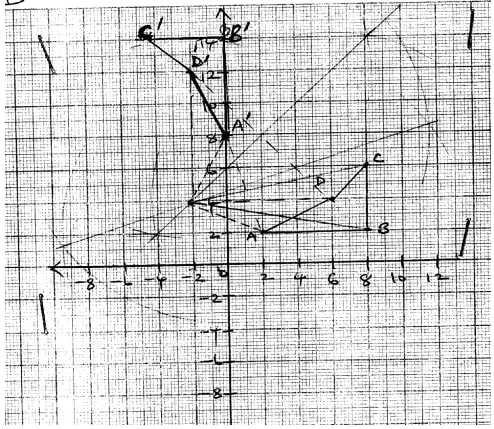
6. Triangle ABC has vertices at A(0, -1), B(4, 3)and C(2,2).
   1. Find the coordinates of image triangle A¹B¹C¹ of triangle ABC under translation 
   2. Given that triangle A¹¹B¹¹C¹¹ is the image of triangle A¹B¹C¹ under an enlargement scale factor 3, centre O(0,0) , find the coordinates of A¹¹, B¹¹and C¹¹
   3. If the area of triangle A¹B¹C¹ is 24 cm², calculate the area of triangle A¹¹B¹¹C¹¹
   4. Find the matrix that maps triangle A¹¹B¹¹C¹¹ onto triangle ABC
7.  
   
   1. The triangle ABC where A (2,-1) B (1, 2) and C (4, 4) is reflected in the line X = 4 to give triangle A¹B¹C¹. Draw the two triangles on the graph provided and state the co-ordinates of A¹B¹C¹
   2. Draw the triangle A² (5,6), B² (2,7) and C² (0,4). Given that triangle A²B²C² is the image of triangle A¹B¹C¹ under rotation, determine the centre and angle of this rotation
   3. Show the image of triangle A²B²C², under an enlargement centre (0, 6) scale factor -1
8.  
   
   1. Find the co-ordinates for the image of point P(6, -2) under the transformation defined by :-
      x¹= x – 3y
      y¹= 2x
   2. 1. A quadrilateral ABCD has vertices A(4, -3), B(2, -3), C(4, -1) and D(5, -4). On the grid provided, draw the quadrilateral ABCD
      2. A¹B¹C¹D¹ is the image of ABCD under a rotation through +90^o about the origin. On the same axes, draw A¹B¹C¹D¹ under the transformation
   3. A²B²C²D²is the image of under A¹B¹C¹D¹ under another transformation by the matrix 
      1. Determine the co-ordinates of A²B²C²D² and plot it on the same axes
      2. Describe the transformation that maps A¹B¹C¹D¹ onto A²B²C²D²
   4. Find a single matrix of transformation that would map A²B²C²D² onto ABCD
9.  
   
   1. Triangle XYZ has vertices X(2, -1) Y(4, -1) and Z (4,2). Triangle XYZ maps onto triangle X¹Y¹Z¹ under transformation T1 =  . Draw triangles XYZ and its image X¹Y¹Z¹ on the grid provided
   2.  Another triangle X¹¹Y¹¹Z¹¹ is the image of X¹Y¹Z¹ after transformation T₂  
      Draw triangle X¹¹Y¹¹Z¹¹ on the same set of axes
   3. Find the single transformation matrix T that maps triangle XYZ on to the final image X¹¹Y¹¹Z¹¹
   4. Given that the area of triangle XYZ is 15cm², find the area of the triangle X¹¹Y¹¹Z¹¹
10. The quadrilateral A (2,1), B (4,1), C (4,4) and D (2,4) is mapped onto A’B’C’D’ by a matrix M₁ such that A¹(8,7), B¹(14,7), C¹(14,16) and D¹(8,16) .
    1. Draw both ABCD and A¹B¹C¹D¹ on the same plane
    2. Find the matrix of transformation that mapped ABCD onto A’B’C’D’ and describe it fully
    3. A¹B¹C¹D¹ underwent another matrix transformation at N which is a translation that gave the image A¹¹B¹¹C¹¹D¹¹, Where A¹¹(7,9), B¹¹(13,9), C¹¹(13,18) and D¹¹(7,18). The transformation N is a translation . Find the translation
    4. Draw A¹¹B¹¹C¹¹D¹¹ on the same axes where ABCD and A¹B¹ C¹D¹ were drawn
11.  
    
    1. On the grid provided. Plot the points A(2, -1) B (0, -3) C(2, -4) and D (4, -2) and join them to form a quadrilateral ABCD. What is the name of this quadrilateral?
    2. The points A¹(1, 2) B¹(3, 0) C¹(4, 2) and D¹(2, 4) are the images of ABC and D under a certain transformation T₁. On the same grid draw quadrilateral A¹B¹C¹D¹ and describe transformation T₁ fully.
    3. The points A¹¹(-2, -4) B¹¹(-6, 0) C1¹(-8, -4) and D¹¹(-4, -8) are the images of A¹B¹C¹D¹ under transformation T2. On the same grid draw quadrilateral A¹¹B¹¹C¹¹D¹¹ and describe the transformation T₂ fully.
    4. On the same grid draw quadrilateral A¹¹¹B¹¹¹C¹¹¹D¹¹¹, the image of A¹¹B¹¹C¹¹D¹¹ under a reflection in the x-axis. State the co-ordinates of A¹¹¹B¹¹¹C¹¹¹D¹¹¹.
12. The Points A¹B¹ and C¹ are the images of A(4, 1), B( 0, -2) and C( -2, 4) respectively under a transformation represented by the matrix;
    M= 
    
    1. Write down the coordinates of A¹B¹ and C¹
    2. A¹¹B¹¹ and C¹¹ are the images of A¹B¹ and C¹ under another transformation whose matrix is:
       N = 
       Write down the coordinates of A¹¹B¹¹ and C¹¹
    3. Transformation M followed by N can be represented by a single transformation P.
       Determine the matrix for
    4. A matrix P is given by 
       Find P^-1
13. Triangle A¹B¹C¹ is the image of triangle ABC under a transformation represented by matrix T =  If the area of triangle A¹B¹C¹ is 25.6cm², find the area of the object
14. A point P(2, -4) is mapped into P¹(4, 0) under a translation.
    Determine the image of point Q(-1, 2) under the same translation
15. The points A (2, 6), B (1, 1), C (2, 3) and D (4,0) are the vertices of quadrilateral ABCD.
    1. On graph paper plot the points A, B, C, and D and join them to form quadrilateral ABCD.
    2. The points A, B, C and D are the images of A¹, B¹, C¹ and D¹ respectively under an enlargement centre the origin and scale factor -2. On the same grid draw the image quadrilateral A¹B¹C¹D¹.
    3. The points A¹¹B¹¹C¹¹ and D11 are the images of ABCD respectively under reflection in the x – axis. On the same grid, locate the pints A¹¹B¹¹C¹¹ and D¹¹ and draw the second image quadrilateral A¹¹B¹¹C¹¹D¹¹.
    4. Quadrilateral A¹¹¹B¹¹¹C¹¹¹D¹¹¹ is the image of ABCD under a certain transformation T.
       Describe transformation T fully.
16. T is a transformation represented by the matrix . Under T, a square of area 10cm² is mapped onto a square 110cm². Find the values of x

Answers

1.  
   1.  
      1. B (4,-5), C (3,6 ½ )
         ∆ ABC drawn
         ∆ ABC drawn
      2. Shear maps
         I (1, 1½ )
         Matrix = 1  0
                      1  1½
   2.  
      1.  
         
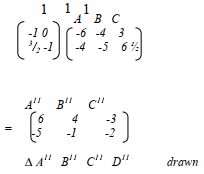
      2. Half turn about (0,0)
2.  
   1. Centre (-2, -2) 90^o
   2. A¹¹ (-2 , -4) , B¹¹ (0, 9)
   3. Half-turn about the centre (0, 2)
      
      
3.  
   1.  
      
   2.  
      
   3. 1. U - - positive three-quarter turn about the origin
      2. UT – Reflection I the line x = 0
         
   4. IdetI = I2.5 x -2 – 1x 0 I= 5
      ∴ Area = 5x(5x2) = 20sq. units
4.  
   1.  
      
   2. Centre (-2, 4)
      Angle +90°
5.  
   
6. A¹ = (0+1, -1-2) = (1, -3)
   B¹ = (4 + 1) , 3-2) = (4, 1)
   C¹ = ( 2 +1, 2-2) = (3-0)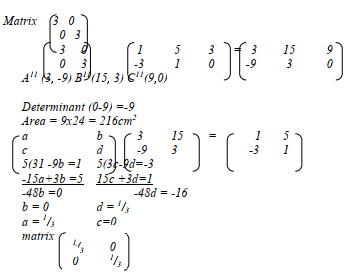
   
   
7. Scale used S₁
   ΔABC drawn B₁
   ΔA₁B₁C₁ drawn B₁
   A(6, -1), B(7, 2), C(4, 4) B₁
   Line x = 4L₁
   ΔA₂ B₂ C₂ drawn B₁
   Two seen B₁
   Centre of rotation
   Angle of centre of rotation B₁
   A₃B₃C₃ drawn B₁
   
   Scale used S₁
   ΔABC drawn B₁
   ΔA₁B₁C₁ drawn B₁
   A, (6, -1), B(7, 2), C(4, 4) B₁
   Line x = 4 L1
   ΔA₂B₂C₂ drawn B₁
   Two seen B₁
   Centre of rotation
   Angle of centre of rotation B₁
   ΔA₃B₃C₃ drawn B₁
8.  
   1. P(6, -2)
      X¹ = 6 -3 (-2) = 12
      Y¹ = 2(6) = 12
      (X¹, Y¹) = (12, 12)
   2. 1. A¹(3, 4)
      2. B¹ (3, 2)
         C¹ (1, 4)
         D¹(4, 3)
   3.  
      
9.  
   
10.  
    
    
11.  
    1. ABCD drawn B₁
       Name – Parallelogram B₁
       
    2. A¹B¹C¹D¹ drawn B₁
       Attempt to joining any two points and bisecting. B¹
       Description – Rotation + 900. B¹ or quarter turn about (0,0)
    3. A¹¹B¹¹C¹¹D¹¹ drawn. B₁
       Description – Enlargement centre (0, 0) Scale factor –Z. B₁
    4. A¹¹¹B¹¹¹C¹¹¹D¹¹¹ – drawn. B₁
       Attempt to reflect. B₁
       Coordinates
       A¹¹¹ = 9-2, 4) C¹¹¹ = (-8, 4) B₁ All correct
       B¹¹¹ = (-6, 0) D¹¹¹ (-4, 8)
12.  
    
13. Det = 2 – 6
    = - 4
    A.S.F = 4
    25.6 = 4
    x
    x = 6.4cm²
    Area of ΔABC = 6.4cm²
14. T + (2) = (4)
          -4       0
    T = (4)  - (2) = (2)
          (0)    (+4)     (4)
    ∴ (2) + (-1) = (1)
       (4)    (2)     (6)
    Q (1,6)
15. 5x² + 6 = ¹¹⁰/₁₀
    5x² + 6 = 11
    x²= 1
    x = ±1