Longitudes and Latitudes Questions and Answers - Form 4 Topical Mathematics

Share via Whatsapp

« Previous Topic
Three Dimensional Geometry Questions and Answers - Form 4 Topical Mathematics

Next Topic »
Linear Programming Questions and Answers - Form 4 Topical Mathematics

Download PDF for future reference Get on Whatsapp for 50/-

Questions

The latitude and longitude of two stations P and Q are (47^oN, 25^oW) and (47^oN, 70^oW) respectively. Calculate the distance in nautical miles between P and Q along the latitude 47^oN
A pane leaves an airport P (10^oS, 60^oE) and flies due north at 800km/hr. By taking radius of the earth to be 6370-km and 1 nautical mile to be 1.853km,
1. Find its position after 2hrs
2. The plane turns and flies at the same speed due West to reach Q longitude 12^oW.
  Find the distance it has traveled due in West nautical miles
3. Find the time it has taken
4. If the local time at P was 1300hrs when it reached Q. Find the local time at Q when it landed at Q
Bot juice company has two types of machines, A and B, for juice production. Type A machine can produce 800 litres per day while type B machine produces 1600 litres per day. Type A machine needs 4 operators and type B machine needs 7 operators. At least 8000 litres must be produced daily and the total number of operators should not exceed 41. There should be 2 or more machines of each type. Let x be the number of machines of type A and y the number of machines for type B,
1. Form all inequalities in x and y to represent the above information
2. On the grid provided below, draw the inequalities and shade the wanted regions
3. Use the grid in (b) to determine the least number of operators required for the maximum possible production
Points R and S are two points on the surface on a latitude 48°S. The two points lie on longitudes 30°W and 150°E respectively. By taking the earth’s radius to be 6370km, calculate:
1. The distance from R to S along a parallel of latitude.
2. An aeroplane flies at an average speed of 2 80km/h from R to S along a great circle through the South Pole. Calculate the total time taken.
3. The local time of R when the local time of R is 2.l5m.
4. Another point Q is 600Nm North of R .Find the location of Q
A jet flies from 34^oN, 12^oE to (34^oE , 24^oE) in 1½ hrs. Find its average speed in knots P and Q are two points on a geographical globe of diameter 50 cm. They both lie on a parallel latitude 50^oNorth. P has longitude 90^oWest and Q has longitude 90o East. A string AB has one end at point P and another at point Q when it is stretched over the North pole. Taking π= 3.142;
1. Calculate the length of the string.
2. If instead the string is laid along the parallel of latitude 50oN with A at point P, calculate the longitude of point B
3. State the position of B if the string is stretched along a great circle of P towards the South pole if point A is static at P.
Two points A(70^o, 15^oE) and B lie on the same circle of latitude on the earths surface. Given that the shortest distance between the two points along the circle of latitude is 2133.6km. Giving coordinates to the nearest degree, find the location of B.
(Take π= ²²/₇ and radius of earth = 6380km)
The position of two towns A and B on the earth’s surface are (36^oN, 49^oE) and (36^oN, 131^oW) respectively (Earth’s radius =6370km and π= ²²/₇):-
1. Find the longitudinal difference between the two towns
2. Calculate the distance between the towns:-
  1. Along a circle of latitude (in km)
  2. Along the great circle in km and nautical miles
3. Another town C, is 840km due East to town B. Locate the position of town C
P, Q and R are points on the surface of the earth such that P (60ºN, 20ºW), Q (60oS, 20^oW) and R(60^oN, 80^oE) find:
1. The shortest distance between P and Q on the surface of the earth in kilometres and nautical miles(nm)
2. The length of latitude 60ºN and hence the length of the minor arc PR in kilometres
3. The distance from P to the North Pole
A jet flies from town X (50^oS, 20^oE) directly to Y(50^oS, 28^oW) and then due South for 1200m to Z
1. 1. Find the latitude of Z
  2. Calculate the distance XY along a parallel of latitude 50^oS in km
2. 1. Given that the average speed of the jet is 400 knots, calculate the time taken to reach Z from X to the nearest 0.1hour
  2. Find the time of arrival at Z given that the plane left X at 7.40a.m. Take π= ²²/7 and radius of the earth to be 6370km
A jet on a rescue mission left town A(35^oS, 15^oE) to town B(45^oN, 15^oE) and then to town C(45^oN, 45^oW). If 1o subtends 60nm and the radius of the earth is 6370km. Find;
1. the distance in nautical miles from A to C via B correct to 4 s.f
2. the distance in kilometers from A to B to the nearest km
3. the jet flew at 840km/h from A to C. If the jet left town A at 8.15a.m, what time will it arrive at town C in local time

Answers

(70 – 25 x 60 = 2700
2700 Cos 47= 2700 x 0.68 = 1841.4nm
1. 22 x 6370 x 2 x α= 1600
  7 360
  α = 14.4^o
  Position (4.4^oN, 60^oE)
2. 72 x 60 cos 4.4^o
  = 4307nm
3. T = D = 4307 x 1.853
  S 800
  = 9.976 hrs
4. Difference in longitude = 72^o
  15^o – 1hr
  ∴ 72^o= 72
  15 = 4.8hrs = 4hrs 48mins behind
  1300hrs
  - 448
  8.12a.m
1. 800 x + 1600 y ≥ 8000
  x + 2y ≥ 10
  4x + 7y ≤ 41
  x ≥ 2
  y ≥ 2
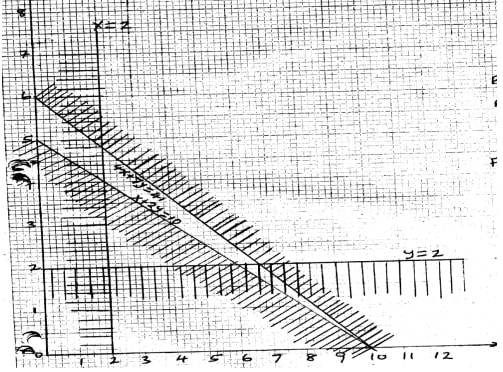
3. for type A = 3 and B = 4
  No. of operators = (3x4) + (4x7)
1. ¹⁸⁰/₃₀₀x 2 x ²²/₇ x 6370 cos 48 = 13,396Km
2. Km = (180 – 96) x 2 x ²²/₇x 6370
  360
  =⁸⁴/₃₆₀x 2 x ²²/₇x 6370 = 9342.7 km
  Time = 9342 = 33.36 km/hr
  280
3. θ= 180°
  
  time = (4 x 180) = 12 hrs
  60
  (14:15 – 12:00) = 2:15a.m
4. 600 Nm
  60
  60°
  Q = (12N, 30W)
1. AB = 80 x 2 x 3.142 x 25
  360
  = 4 x 25 x 3.142
  9
  =314.2 cm
  9
  = 34.9111 cm.
2. θ x 2 x 3.142 x 25cos 50^o= 314.2
  360 9
  θ= 314.2 x 360
  9
  50 x 3.142 x cos 50
  = 93.35^o
  Longitude of BC(93.35^o– 90^o)E
  = 03.350E.
3. θ x 3.142 x 50 = 314.2
  360 9
  θ = ^314.2/₉ x 360
  3.142 x 50
  = 80^o
  Latitude of B (80^o– 50) S
  = 30^oS
  Position of B ⇒ (30^oS, 03.35^oE
2133.6 = x x 2 x 22 x 6380 cos 70^o
360 7
α = 21.33 x 6 x 360 x 7
44 x 6380 x cos 70^o
α+ 15^o= 56^o
= 56 – 15 = 41^oN
∴ Location of B is B(70^oS, 41^oN
1. Longitudinal diff = 180^o
2. 1. ¹⁸⁰/₃₆₀x 2 x ²²/₇x 6370 x cos 360^o
    = 16196.52m
  2. ¹⁸⁰/₃₆₀x 2 x ²²/₇x 6370
    = 12012km
3. ^θ/₃₆₀ x 2x ²²/₇x 6370 cos 36= 840
  = 9.3353^o
  = position C = 131-9.3^oW
  C(36^oN, 121.7^oW)
1. PQ = ¹²⁰/₃₆₀πx 6370 x 2
  =²⁴⁰/₃₆₀πx²²/7x 6370 = 13,346.6
2. 2PR cos 60°
  PR = ¹⁰⁰/360x2 x 6370 cos 60
  =²⁰⁰/₃₆₀x²²/₇x 6370 cos 60 = 5561.1km
3. PN = ³⁰/₃₆₀x2 x ²²/₇x 6370
  = 3336.67 km
1. 1. 60 (z -50) = 1200
    Z = 20
    Z = 70^oS
  2. xy = 48 x 2 x 6370 cos 50
    360
    = 3431.629km
2. 1. XZ = 3431. 627 + 1200
    1.853
    = 3051.9km
    Time = 3051.9 = 7.6hrs
    400
  2. tie = 7.36 + 4.28 = 12.04
1. A – B = 45 + 35 = 80^o Lat. Diff
  = 80 X 60 = 4800nm
  B – C = 15 + 45 = 60^olong. Diff
  = (60 X 60 X cos 45
  = 3600 X 0.7071 = 2545.56nm
  Total distance = ( 4800 + 2525.56)nm
  = 7345.56nm
  302
  ≈7346nm (4.s.f)
2. 80 X 2 X 22 X 6370
  360 7
  = 88 x 910
  9
  = 8897.78 km
  ≈8898km ( to nearest km)
3. B- C = 60 X 2 X 22 X 6370 X cos 450
  360 7
  = 22 X 910 X 0.7071
  6
  = 471.8.7 km
  A – C in Km = ( 8898 + 4718.70
  =13616.7 km
  Time taken = 13616.7 = 16.21 hours
  840
  = 16 hrs 13min
  Arrival time = 08.15 + 16.13 = 24.28
  = 12.28 am following morning