- Introduction
- Approximating Area by Trapezium Method.
- The Mid - Ordinate Rule
- Past KCSE Questions on the Topic.

Introduction
- Estimation of areas of irregular shapes such as lakes, oceans etc. using counting method. The following steps are followed
- Copy the outline of the region to be measured on a tracing paper
- Put the tracing on a one centimeter square grid shown below
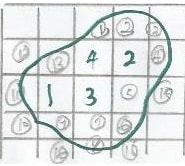
- Count all the whole squares fully enclosed within the region
- Count all the partially enclosed squares and take them as half square centimeter each
- Divide the number of half squares by two and add it to the number of full squares.
Number of compete squares = 4
Number of half squares = 16/2 = 8
Therefore the total number of squares = 25 + 8 = 33
The area of the land mass on the paper is therefore 33 cm2
Note; - The smaller the subdivisions, the greater the accuracy in approximating area.

Approximating Area by Trapezium Method.
- Find the area of the region shown, the region may be divided into six trapezia of uniform as shown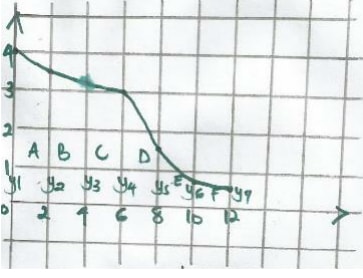
- The area of the region is approximately equal to the sum of the areas of the six trapezia.
Note;
- The width of each trapezium is 2 cm, and 4 and 3.5 are the lengths of the parallel sides of the first trapezium.
The area of the trapezium A = ½ x 2(4+3.5) = 7.5 cm2
Area of the trapezium B = ½ x 2(3.5+3.5) = 6.7 cm2
Area of the trapezium C = ½ x 2(3+1.5) = 6.2cm2
Area of the trapezium D = ½ x 2(3+1.5) = 4.5 cm2
Area of the trapezium E = ½ x 2(1.5+0.8) = 2.3 cm2
Area of the trapezium F = ½ x 2(0.8+3.5) = 1.3 cm2
Therefore, the total area of the region is
(7.5 +6.7 +6.2 +4.5 +2.3 +1.3)cm2 = 28.5 cm2
- If the lengths of the parallel sides of the trapezia (ordinates) are y1, y2 ,y3 ,y4 ,y5, y6 y7
Note;
- In trapezium rule, except for the first and last lengths, each of the other lengths is counted twice. Therefore, the expression for the area can be simplified to:
½ x 2 {(y1+ y7)+2 (y2+ y3+ y4+ y5+ y6)}
In general, the approximate area of a region using trapezium method is given by:
A =½h{(y0+ yn)+2(y1+ y2+ y3+…………. yn-1 )}
Where h is the uniform width of each trapezium,
y0 - yn are the first and last length respectively.
- This method of approximating areas of irregular shape is called trapezium rule.
Example
A car start from rest and its velocity is measured every second from 6 seconds.
| Time (t) |
0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Velocity v ( m/s |
0 | 12 | 24 | 35 | 41 | 45 | 47 |
Use the trapezium rule to calculate distance travelled between t = 1 and t = 6
Note;
- The area under velocity – time graph represents the distance covered between the given times.
- To find the required displacement, we find the area of the region bounded by graph, t =1 and t =6
Solution
Divide the required area into five trapezia, each of with 1 unit. Using the trapezium rule;
A = ½ h{(y1+ y6)+2 (y2+ y3+ y4+y5 )}
The required displacement = ½h{(12+47 ) + 2( 24+35+41+45 )}
= ½( 59 + 2 x145 )
= 174.5 m
Example
Estimate the area bounded by the curve y = ½x2 + 5, the x – axis, the line x =1 and x = 5 using the trapezium rule.
Solution
To plot the graph y = ½x2 + 5, make a table of values of x and the corresponding values of y as follows:
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y = ½x2 + 5 |
5 | 5.5 | 7 | 9.5 | 1 3 | 1 7.5 |
By taking the width of each trapezium to be 1 unit, we get 4 trapezia A, B , C and D .The area under curve is approximately;
A = ½h{(y1+ y5)+2(y2 + y3+ y4 )}
= ½(5.5+ 17.5)+ 2(7 + 9.5 + 13) sq.units
= 1 sq.units
½(23.0+59)
= 41 sq.units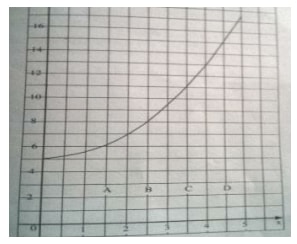

The Mid - Ordinate Rule
- The area OPQR is estimated: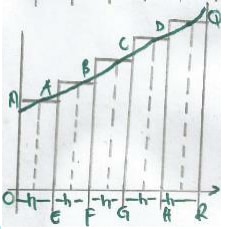
- The area of OPQR is estimated as follows
- Divide the base OR into a number of strips, each of their width should be the same .In the example we have 5 strips where
h = length of the base OR
number of strips - From the midpoints of OE ,EF ,FG ,GH and HR , draw vertical lines ( mid- ordinates) to meet the curve PQ as shown above
- Label the mid-ordinates y1,y2,y3,y4 and y5
- We take the area of each trapezium to be equal to area of a rectangle whose width is the length of interval (h) and the length is the value of mid –ordinates. Therefore, the area of the region OPQR is given by;
A = (y1×h) + (y2 ×h) + (y3×h) + (y4 ×h) + (y5 ×h)
= h (y1 + y2 + y3 + y4 + y5 )
- This the mid –ordinate rule h(y1 + y2 + y3 + y4 + y5).
Note:
The mid-ordinate rule for approximating areas of irregular shapes is given by ;
Area = (width of interval) x (sum of mid – ordinates)
Example
Estimate the area of a semi-circle of radius 4 cm using the mid – ordinate rule with four equal strips, each of width 2 cm.
Solution
The above shows a semicircle of radius 4 cm divided into 4 equal strips, each of width 2 cm. The dotted lines are the mid-ordinates whose length are measured.
By mid- ordinate rule;
= h (y1 + y2 + y3 + y4 + y5 )
= 2 (2.6 + 3.9 + 3.9 + 2.6)
= 2 x 13
= 26 cm2
The actual area is πr2 = 3.142 ×42
2
= 25.14 cm2 to 4 s.f
Example
Estimate the area enclosed by the curve y =½ x2 + 1 , x = 0, x = 3 and the x – axis using the mid-ordinate rule.
Solution
Take 3 strips. The dotted lines are the mid – ordinate and the width of each of the 3 strips is 1 unit.
By calculation, y1 ,y2 and y3 are obtained from the equation;
y =½ x2 + 1
When x = 0.5, y1 = 1/2 x(0.5)2 + 1
= 1.125
When x = 1.5, y1 = 1/2 x(1.5)2 + 1
= 2.125
When x = 2.5, y1 = 1/2 x(0.5)2 + 1
= 4.125
Using the mid ordinate rule the area required is
A = 1 (y1 + y2 + y3)
= 1(1 .125 + 2.125 + 4.125)
= 7.375 square units

Past KCSE Questions on the Topic.
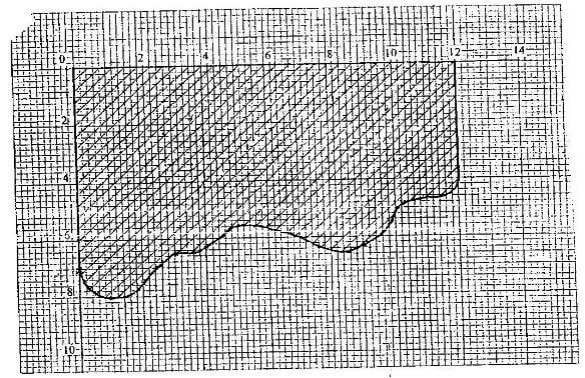
- The shaded region below represents a forest. The region has been drawn to scale where 1 cm represents 5 km. Use the mid – ordinate rule with six strips to estimate the area of forest in hectares. (4 marks)
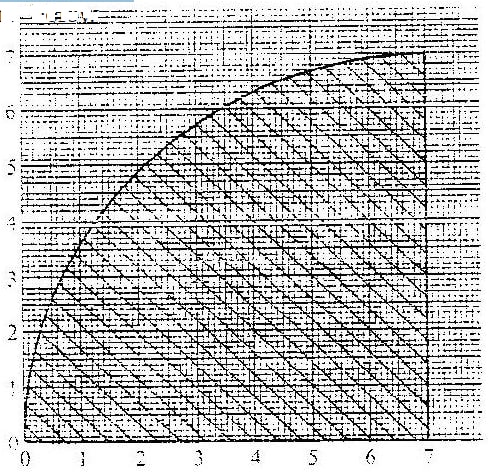
- Find the area bounded by the curve y=2x3 – 5, the x-axis and the lines x=2 and x=4.
- Complete the table below for the function y=3x2 – 8x + 10 (1 mk)
Using the values in the table and the trapezoidal rule, estimate the area bounded by the curve y= 3x2– 8x + 1 0 and the lines y=0, x=0 and x=104.x 0 2 4 6 8 10 y 10 6 70 230 - Use the trapezoidal rule with intervals of 1 cm to estimate the area of the shaded region below
-
- Find the value of x at which the curve y= x – 2x2 – 3 crosses the x - axis
- Find ∫(x2 – 2x – 3)dx
- Find the area bounded by the curve y = x2 – 2x – 3, the axis and the lines x= 2 and x = 4.
- The graph below consists of a non- quadratic part (0 ≤ x ≤ 2) and a quadrant part (2 ≤ x 8). The quadratic part is y = x2 – 3x + 5, 2 ≤ x ≤ 8
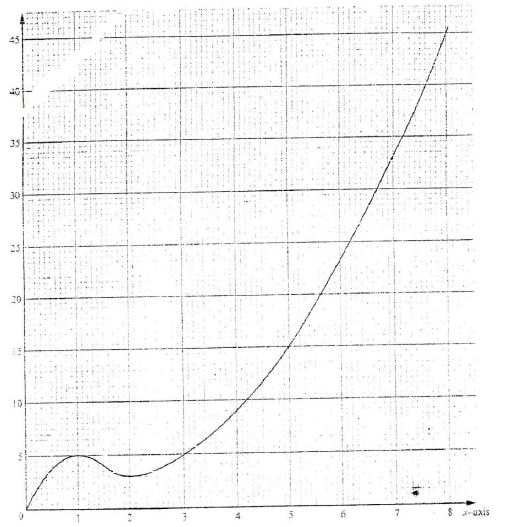
- Complete the table below
(1 mk)x 2 3 4 5 6 7 8 y 3 - Use the trapezoidal rule with six strips to estimate the area enclosed by thecurve, x = axis and the line x = 2 and x = 8 (3mks)
- Find the exact area of the region given in (b) (3mks)
- If the trapezoidal rule is used to estimate the area under the curve between x = 0 and x = 2, state whether it would give an under- estimate or an over- estimate. Give a reason for your answer.
- Complete the table below
- Find the equation of the gradient to the curve Y= (x2 + 1 ) (x – 2) when x = 2
- The distance from a fixed point of a particular in motion at any time t seconds is given by
S = t3 – 5t2 + 2t + 5
2t2
Find its:- Acceleration after 1 second
- Velocity when acceleration is Zero
- The curve of the equation y = 2x + 3x2, has x = -2/3 and x = 0 and x intercepts. The area bounded by the axis x = -2/3 and x = 2 is shown by the sketch below.
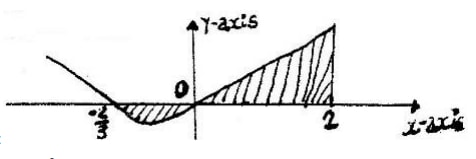
Find:- (2x + 3x2) dx
- The area bounded by the curve x – axis, x = - 2/3 and x =2
- A particle is projected from the origin. Its speed was recorded as shown in the table below
Use the trapezoidal rule to estimate the distance covered by the particle within the 35 seconds.Time (sec) 0 5 1 0 1 5 20 25 39 35 Speed (m/s) 0 2.1 5.3 5.1 6.8 6.7 4.7 2.6 - The gradient function of a curve is given by dy/dx = 2x2 – 5. Find the equation of the curve, given that y = 3, when x = 2
- The velocity, vm/s of a moving particle after seconds is given: v = 2t3 + t2 – 1 . Find the distance covered by the particle in the interval 1 ≤ t ≤ 3
- Given the curve y = 2x3 + 1/2x2 – 4x + 1 . Find the:
- Gradient of curve at {1 , -1/2}
- Equation of the tangent to the curve at {1, - 1/2}
- The diagram below shows a straight line intersecting the curve y = (x-1)2 + 4 At the points P and Q. The line also cuts x-axis at (7, 0) and y axis at (0, 7)
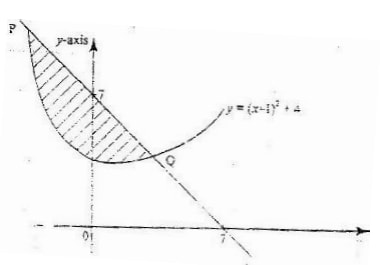
- Find the equation of the straight line in the form y = mx +c.
- Find the coordinates of p and Q.
- Calculate the area of the shaded region.
- The acceleration, a ms-2, of a particle is given by a =25 – 9t2, where t in seconds after the particle passes fixed point O. If the particle passes O, with velocity of 4 ms-1, find
- An expression of velocity V, in terms of t
- The velocity of the particle when t = 2 seconds
- A curve is represented by the function y = 1/3 x3 + x2 – 3x + 2
- Find dy/dx
- Determine the values of y at the turning points of the curve y = 1/3x3 + x2 – 3x + 2
- In the space provided below, sketch the curve of y = 1/3 x3 + x2 – 3x + 2
- A circle centre O, ha the equation x2 + y2 = 4. The area of the circle in the first quadrant is divided into 5 vertical strips of width 0.4 cm
- Use the equation of the circle to complete the table below for values of y
correct to 2 decimal places
X 0 0.4 0.8 1 .2 1 .6 2.0 Y 2.00 1.60 0 - Use the trapezium rule to estimate the area of the circle
- Use the equation of the circle to complete the table below for values of y
- A particle moves along straight line such that its displacement S metres from a given point is S = t3 – 5t2 + 4 where t is time in seconds
Find- The displacement of particle at t = 5
- The velocity of the particle when t = 5
- The values of t when the particle is momentarily at rest
- The acceleration of the particle when t = 2
- The diagram below shows a sketch of the line y = 3x and the curve y = 4 – x2 intersecting at points P and Q.
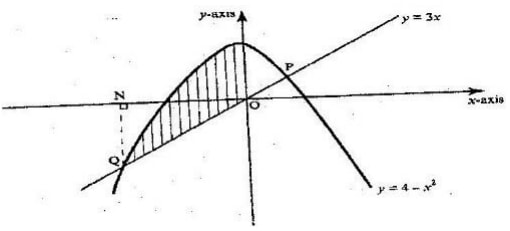
- Find the coordinates of P and Q
- Given that QN is perpendicular to the x- axis at N, calculate
- The area bounded by the curve y = 4 – x2, the x- axis and the line QN (2 marks)
- The area of the shaded region that lies below the x- axis
- The area of the region enclosed by the curve y = 4 – x2, the line y – 3x and the y-axis.
- The gradient of the tangent to the curve y = ax3 + bx at the point (1 , 1 ) is -5. Calculate the values of a and b. 2007
- The diagram on the grid below represents as extract of a survey map showing two adjacent plots belonging to Kazungu and Ndoe. The two dispute the common boundary with each claiming boundary along different smooth curves coordinates (x, y1) and (x, y2) in the table below, represents points on the boundaries as claimed by Kazungu Ndoe respectively.
X 0 1 2 3 4 5 6 7 8 9 Y1 0 4 5.7 6.9 8 9 9.8 10.6 11.3 12 Y2 0 0.2 0.6 1.3 2.4 3.7 5.3 7.3 9.5 12 - On the grid provided above draw and label the boundaries as claimed by Kazungu and Ndoe.
-
- Use the trapezium rule with 9 strips to estimate the area of the section of the land in dispute
- Express the area found in b (i) above, in hectares, given that 1 unit on each axis represents 20 metres
- The gradient function of a curve is given by the expression 2x + 1 . If the curve passes through the point (-4, 6);
- Find
- The equation of the curve
- The vales of x, at which the curve cuts the x- axis
- Determine the area enclosed by the curve and the x- axis
- Find
- A particle moves in a straight line through a point P. Its velocity v m/s is given by v= 2 – t, where t is time in seconds, after passing P. The distance s of the particle from P when t = 2 is 5 metres. Find the expression for s in terms of t.
- Find the area bonded by the curve y=2x – 5 the x-axis and the lines x=2 and x = 4.
- Complete the table below for the function
Y = 3x2 – 8 x + 1 0
Using the values in the table and the trapezoidal rule, estimate the area bounded by the curve y = 3x2 – 8x + 1 0 and the lines y – 0, x = 0 and x = 1 0X 0 2 4 6 8 1 0 Y 1 0 6 - 70 - 230 -
- Find the values of x which the curve y = x2 – 2x – 3 crosses the axis
- Find (x2 – 2 x – 3) dx
- Find the area bounded by the curve Y = x2 – 2x – 3. The x – axis and the lines x = 2 and x = 4
- Find the equation of the tangent to the curve y = (x + 1 ) (x - 2) when x = 2
- The distance from a fixed point of a particle in motion at any time t seconds is given by s = t – 5/2t2 + 2t + s metres
Find its- Acceleration after t seconds
- Velocity when acceleration is zero
- The curve of the equation y = 2x + 3x2, has x = - 2/3 and x = 0, as x intercepts. The area bounded by the curve, x – axis, x = -2/3 and x = 2 is shown by the sketch below.
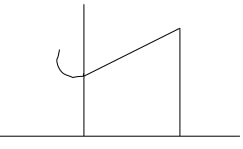
- Find ∫(2x + 3x2) dx
- The area bounded by the curve, x axis x = -2/3 and x = 2
- A curve is given by the equation y = 5x3 – 7x2 + 3x + 2
Find the- Gradient of the curve at x = 1
- Equation of the tangent to the curve at the point (1 , 3)
- The displacement x metres of a particle after t seconds is given by x = t2 – 2t + 6, t> 0
- Calculate the velocity of the particle in m/s when t = 2s
- When the velocity of the particle is zero,
Calculate its- Displacement
- Acceleration
- The displacement s metres of a particle moving along a straight line after t seconds is given by s =3t + 3/2t2 – 2t3
- Find its initial acceleration
- Calculate
- The time when the particle was momentarily at rest.
- Its displacement by the time it comes to rest momentarily when t = 1 second, s = 1½ metres when t = ½ seconds
- Calculate the maximum speed attained
Download Area Approximation - Mathematics Form 4 Notes.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

