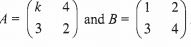Kenya Certificate Of Secondary Education (KCSE 2008) Mathematics Paper 1 ^Featured

SECTION I (50 marks)

    Answer all the questions in this section.

1. Without using  a calculator, evaluate   (2 marks)
2. Simplify   (3 marks)
3. Simplify the expression  (3 marks)
   
   
4. Mapesa travelled by train from Butere to Nairobi. The bus left Butere on Sunday at 23:50 hours and travelled for 7 hours 15 minutes to reach Nakuru. After a 45 minutes stop at Nakuru, the train took 5 hours 40 minutes to reach Nairobi. 
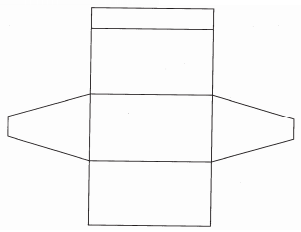
   Find the time, in the 12 hour clock system and the day Mapesa arrived in Nairobi. (2 marks)
   
   
5. The figure below shows the net of a solid. 

     
   Below is a part of the sketch of the solid whose net is shown above. Complete the sketch of the solid, showing the hidden edges of the broken lines. (3 marks)       
   
    

6. A fuel dealer makes a profit of ksh 520 for every 1000 litres of petrol sold and Ksh 480 for every 1000 litres of diesel sold. 
   In a certain month, the dealer sold twice as much diesel as petrol. If the total fuel sold that month was 900 000 litres, find the dealer's profit for that month. (3 marks)
   
   
7. A liquid spray of mass 384 g is packed in a cylindrical container of internal radius 3.2 cm. 
   Given the density of the liquid is 0.6 g/cm³, calculate to 2 decimal places the height of the liquid in the container.  (3 marks)
   
   
8. Line BC below is a side of triangle ABC and also a side of a parallelogram BCDE.
      
   Using a ruler and compasses only, construct:
   1. The triangle ABC given that ∠ ABC = 120° and AB = 6 cm. (1 mark)
   2. The parallelogram BCDE whose area is equal to that of the triangle ABC and point E us on line AB. (3 marks)
      
      
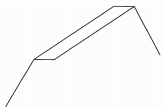
9. A solid metal sphere of radius 4.2 cm was melted and the molten material used to make a cube.
   Find to 3 significant figures the length of the side of the cube. (3 marks)
   
   
10. An angle 1.8 radians at the centre of a circle subtends an arc of length 23.4 cm.
    Find: 
    1. the radius of the circle. (2 marks)
    2. the area of the circle enclosed by the arc and the radii. (2 marks)
       
       
11. Three vertices of a rhombus ABCD are A(-4, -3), B(1, -1) and C(3, 4).
    
    1. Draw a rhombus on the grid provided below. (2 marks) 
        
    2. Find the equation of line Ad in the form of y = mx + c, where m and c are constant. (2  marks)
       
       
12. Two matrices A and B are such that 
    Given that the determinants of AB = 4, find the value of k. (3 marks)
    
    
13. A rectangular and two circular cut-outs of metal sheets of negligible thickness are used to make a closed cylinder. The rectangular cut-out has a height of 18 cm. Each circular cut-out has a radius of 5.2 cm. Calculate the terms in ∏, the surface area of the cylinder. (3 marks)
    
    
14. Given that log 4 = 0.6021 and log 6 = 0.7782, without using mathematical tables or a calculator, evaluate log 0.096. (3 marks)
    
    
15. The equation of a line L₁ is 2y - 5x - 8 = 0 and line L₂ passes through the lines (-5, 0) and (5, -4). 
    Without drawing the lines L₁ and L₂, show that the two lines are perpendicular to each other. (3 marks)
    
    
16. Solve the equation:
      (4 marks)

    
    SECTION II (50 marks)

    Answer any five questions from this section. 

17. 1. The ratio of Juma's and Akinyi's earnings was 5:3. Juma's earnings rose to Kshs 8 400 after an increase of 12%.
       Calculate the percentage increase in Akinyi's earnings given that the sum of their new earnings was Ksh 14 100. (6 marks)
    2. Juma and Akinyi contributed all the new earnings to buy maize at Ksh 1 175 per bag. The maize were then sold at Ksh 1 762. 50 per bag. The two sahred all the money from the sales of the maize in the ratio of their contributions.
       Calculate the amount that Akinyi got. (4 marks)
       
       
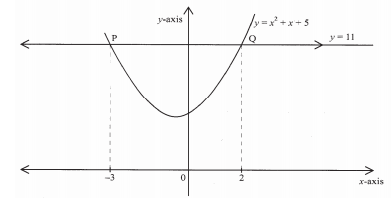
18. The figure below is a sketch of a curve whose equation is y = x² + x + 5.
    It cuts the line y=11 at points P and Q.
       
    1. find the area bound by the curve y = x² + x + 5 line y = 11 using the trapezium rule with 5 strips. (5 marks)
    2. Calculate the difference in the area if the mid-ordinate rule was used instead of the trapezium rule. (5 marks)
       
       
19. In the figure below AB =p, AD = q, DE = ¹/₂AB and BC = ²/₃BD
    
       
    
    1. Find in terms of p and q the vectors:
       1. BD; (1 mark) 
       2. BC; (1 mark)
       3. CD; (1 mark)
       4. AC. (1 mark)
    2. Given that AC = kCE, where k is scalar, find:
       1. the value of k; (4 marks)
       2. the ratio in which C divides AE. (1 mark)
          
          
20. The diagram below represents two vertical watch-towers AB and CD on a level ground. P and Q are two points on a staright road BD. The height of the tower AB is 20 m and road BD is 200 m. 
     
    1. A car moves from B towards D. At point P, the angle of depression of the car from point A is 11.3°. Calculate the distance BP to 4 significant figures. (2 marks)
    2. If the car takes 5 seconds to move from P to Q at an average speed of 36km/h, calculate the of depression of Q from Ato 2 decimal places. (3 marks)
    3. Given that QC = 50.9 m, calculate:
       1. the height of CD in metres to 2 decimal places; (2 marks)
       2. the angle of elevation of A from C to the nearest degree. (3 marks)
          
          
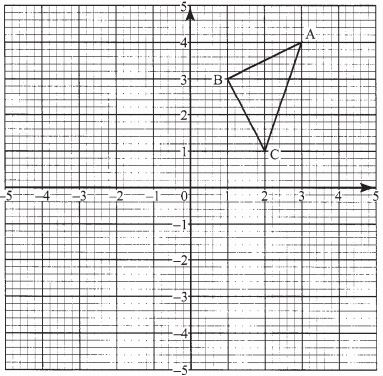
21. The diagram below shows a triangle ABC with A(3, 4), B(1, 3) and C(2, 1).

    

    1. Draw ΔA'B'C', the image of ΔABC under a rotation of +90° about (0, 0). (2 marks)
    2. Draw ΔA''B''C'' the image of ΔA'B'C' under a reflection in the line y = x. (2 marks)
    3. Draw ΔA'''B'''C''', the image ΔA''B''C'' under rotation of -90^o about (0, 0) (2 marks)
    4. Describe a single transformation that maps ΔABC ontoΔA'''B'''C'''. (2 marks)
    5. Write down the equation of the lines of symmetry of the quadrilateral BB''A'''A'. (2 marks)
       
       
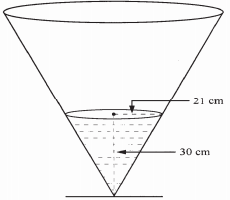
22. The diagram below represents a conical vessel which stands vertically. The vessel contains water to a depth of 30 cm. The radius of the water surface in the vessel is 21 cm. (Take ∏ = ²²/₇)

    

    1. Calculate the volume of the water in the vessel in cm³. (2 marks)
    2. When a metal sphere is completely submerged in the water, the level of the water in the vessels rise by 6 cm.

       Calculate:

       1. The radius of the new water surface in the vessel; (2 marks)
       2. The volume of the metal sphere in cm³; (3 marks)
       3. The radius of the sphere. (3 marks) 
          
          
23. A group of people planned to contribute equally towards a water project which needed Ksh 2 000 000 to complete. However, 40 members of the group withdrew from the project. As a result, each of the remaining results were to contribute Ksh2 500 more.
    1. Find the original number of members in the group. (5 marks)
    2. Forty five percent the value of the project was founded by Constituency Development Fund (CDF). Calculate the amount of the contribution that would made by each of the remaining members of the group. (3 marks)
    3. Members' contributions were in terms of labour provided and money contributed. If the ratio of the value of labour to the money contributed was 6:19, calculate the amount of money contributed by the members. (2 marks)
       
       
24. The distance s metres from a fixed point O, covered by a particle after t seconds is given by the equation:

    s = t³ + 6t² + 9t + 5

    1. Calculate the gradient to the curve at t  = 0.5 seconds. (3 marks)
    2. Determine the values of s at the maximum and minimum turning points of the curve. (4 marks)
    3. On the space provided, sketch the curve of s = t³ - 6t² + 9t + 5. (3 marks)