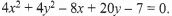Kenya Certificate Of Secondary Education (KCSE 2008) Mathematics Paper 2

 SECTION I

Answer all the questions in this section

1.  In this question, show all the steps in your calculations, giving the answer at each stage. Use logarithms correct to four decimal place, to evaluate.
      (3 marks)
2. Make h the subject formula 
             (2 marks)
3. Line AB given below is one side of triangle ABC. Using a ruler and a compasses only:
        
   1. Complete the triangle ABC such that BC = 5 cm and angle ABC = 45°. (1 mark)
   2.  On the same diagram construct  atriangle touching sides AC, BA produced and BC produced. (2 marks)
4. The position vectors of points A and B are  respectively. A and P are divides AB in the ratio 2:3.
    Find the position vector of point  P. (3 marks)
5. The top of  a table is a rectangular hexagon. each side of the hexagon measures 50.0 cm. Find the maximum percentage error in calculating the the perimeter of the top of the table. (3 marks)
6. A student at a certain college has 60% chance of passing an examination at the first attempt. Each time a student fails and repeats the examination, his chances of passing are increased by 15%. 
   Calculate the probability that a student in college passes an examination at the second or at the third attempt. (3 marks)
7. An aeroplane flies at an average speed of 500 knots due East from point P(53.4^oN, 40^oE) to another point Q. It takes 2¼ hours to reach point Q.
   Calculate:
   1. the distance in nautical miles it travelled; (1 mark)
   2. the longitude of point Q to 2 decimal places. (2 marks)
8. 1. Expand and simplify the expression.                 (2 marks)
   2. Use the expansion in (a) above to find the value of 14⁵. (2 marks)
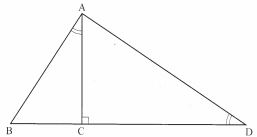
9. In the figure below, angles BAC and ADC are equal. Angle ACD is a right angle. The ratio of the sides AC: BC = 4:3.  
      
   Given that the area of the traingle ABC is 24 cm², find the area of triangle ACD. (3 marks)
10.  Points A(2, 2) and B(4, 3) are mapped onto A'(2, 8) and B' (4, 15) respectively by the transformation T.
    Find the matrix of T. (4 marks)
11. The equation of a circle given by 
    Determine the coordinates of the centre of the circle. (3 marks)
    
    
12.  Solve for y in the equation   (3 marks)
    
    
13. Without using a calculator or mathematic tables, express  in surd form and simplify. (3 marks)
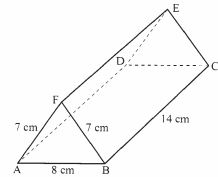
14. The figure below represents a triangular prism. The faces ABCD, ADEF and CBFE are rectangles.
    AB = 8 cm, BC = 14 cm, BF = 7 cm and AF = 7 cm.  
       
    Calculate the angle between the faces BCEF and ABCD. (3 marks)
15. A particle moves in a straight line from a fixed point. Its velocity Vms^-1 after t seconds is given by V = 9t² - 4t + 1.
    Calculate the distance travelled by the particle during the third second. (3 marks)
16.  Find in the radians, the values of x in the interval 0^o≤ x ≤ 2π^o for which 2 cos²x - sin x = 1
    ( Leave the answers in terms of π)        (4 marks)

    SECTION II (50 MARKS)

    Answer any five questions in this section. 

17.  A trader deals in two types of rice; type A and type B. Type A costs Ksh 400 per bag while type B costs Ksh 350 per bag.
    1. The trader mixes 30 bags of type A with 50 types of type B. If he sells the mixture at a profit of 20%, calculate the the selling price of one bag of the mixture. (4 marks)
    2. The trader now mixes type  A with B in the ratio x:y respectively.  If the cost of the mixture is 383.50 per bag, find the ratio x:y. (4 marks)
    3. The trader mixes one bag of the mixture in part (a)with one bag of the mixture in part (b) above. 
       Calculate the ratio of type A rice to type B rice in this mixture. (2 marks)
       
       
18. Three variables p, q and r are such that p varies directly as q and inversely as the square of r.
    1. When p = 9, q = 12 and r = 2. 
       Find p when q = 15 and r = 5.     (4 marks)
    2. Express q in terms of p and r. (1 mark)
    3. If p is increased by 20% and r is decreased by 10%, find:
       
       1. a simplified expression for the change in q in terms of p and r. (3 marks)
       2. the percentage change in q. (2 marks)
          
          
          
19. 1. Complete the table below, giving the correct values correct to two decimal places.
        (2 marks)
    2. On the grid provided, draw the graphs of y = sin 2x  and y = 3cosx - 2  for 0^o≤ x ≤360^o on the same axes.
       Use the scale of 1 cm to represent 30^o on the x-axis and 2 cm to represent 1 unit on the y-axis. (5 marks)
       
    3. Use the graph in (b) above to solve the equation y = 3cosx - sin2x = 2. (2 marks)
       
    4. State the ampitude of y = 3cosx - 2. (1 mark)
       
       
       
20. In the figure below, DA is the diameter of the circle ABCD centre O, radius 10 cm. TCS is a tangent to the circle at C, AB = BC and angle DAC = 38^o.
    1.  
    2. F
    3. ind the size of angle:
    4. 2. ACS; (2 marks)
       3. BCA. (2 marks)
          
          
    5. Calculate the length of:
       1. AC; (2 marks)
       2. AB. (4 marks)
21. Two policemen were walking together at a road junction. each had a walkie talkie. The maximum distance at which one could communicate with the other was 2.5 km.
    One of the policemen walked due East at 3.2 km/h while the other walked North at 2.4 km/h. The policeman who headed East travelled for x km while the other one who headed North travelled for y km before they were unable to communicate.
    
    1. Draw a sketch to represent the relative positions of the policemen. (1 mark)
    2. 1. From the information above, form two simultaneous equations in x and y. (2 marks)
       2. Find the values of x and y. (5 marks)
       3. Calculate the time taken before the policmen were unable to communicate. (2 marks)
          
          
22. The table below shows the distribution of marks scored by 60 pupils in a test.
     
    
    1. On the grid provided, draw an ogive that represents the above information. (4 marks)

       

    2. Use the graph to estimate the interquartile range of this information. (3 marks)
    3. In order to pass the test, a pupil had to score more than 48 marks. Calculate the percentage of pupils who passed the test. (3 marks)
       
       
23. Halima deposited Ksh 109 375 in a financial institution which paid simple interest at the rate of 8% p.a. At the end of 2 years, she withdrew all the money. She then invested the money in shares. The value of the shares depriciated at 4% p.a. during the first year of investment. In the next 3 years, the value of the shares appreciated at the rate of 6% every four months.
    
    1. Calculate the amount Halima invested in shares. (3 marks)
    2. Calculate the value of Halima shares:
       
       1. at the end of the first year; (2 marks)
       2. at the end of the fourth year to the next shilling. (3 marks)
    3. Calculate Halima's gain from the shares as percentage. (2 marks)
       
       
24. The table below shows the values of x and some of the values of y for the curve y = x³ + 3x² -4x -12 in the range  -4 ≤ x ≤2.
    1. Complete by filling in the missing values of y.
       (2 marks)
    2. On the grid provided, draw the graph y = x³ + 3x² -4x -12 for -4 ≤ x ≤2.
       Use the scale Horizontal axis 2 cm for 1 unit and vertical axis 2 cm for 5 units. (3 marks)
       
    3. By drawing a suitable straigh line on the same grid as (b) above, solve the equation:
       x³ + 3x² - 5x - 6= 0.                                      (5 marks)