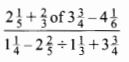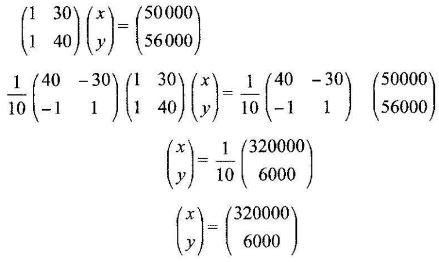KCSE 2011 Mathematics Paper 1 with Marking Scheme

SECTION A (50 marks)
Answer all the questions in this section.

1. Without using a calculator, evaluate; ( 3 marks)
   
2. The diagonal of a rectangular garden measures 11¹/₄ m while its width measures 6³/₄ m.
   Calculate the perimeter of the garden. (2 marks)
3. A motorist took 2 hours to travel from one point to another town and 1 hour 40 minutes to travel back. Calculate the percentage change in the speed of the motorist. (3 marks)
4. A square room is covered by a number of a whole rectangular slabs of sides 60 cm by 42 cm.
   Calculate the least possible area of the room in square metres. (3 marks)
5. Given that sin (x+60)⁰ = cos (2x)⁰, find the tan (x+60)⁰  (3 marks)
6. Simplify the expression: (3 marks)
   
7. The external length, width and height of an open rectangular container are 41 cm, 21 cm and 15.5 cm respectively. The thickness of the material making the container is 5 mm. If the container is has 8 litres of water, calculate the internal height above the water level. (4 marks)
8. Factorize 2x²y² - 5xy - 12 (2 marks)
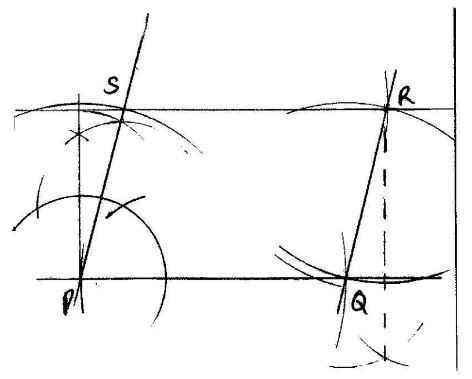
9. Using a ruler and a pair of compasses only,:
   1. Construct a parallelogram PQRS in which PQ = 6 cm, QR = 4 cm and angle SPQ = 75⁰; (3 marks)
   2. Determine the perpendicular distance between PQ and SR. (1 mark)
10. The masses of people during a clinic session were recorded as shown in the table below.
    
    Calculate the mean mass. (3 marks)
11. A customer paid Ksh 5 880 for a suit after she was allowed a discount f 2% on the selling price. If the discount had not been allowed on, the shopkeeper would have made a profit of 20% on the sale of the suit. Calculate the price on which the shopkeeper bought the suit. (3 marks)
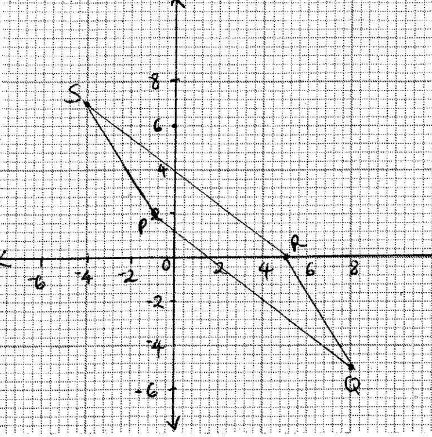
12. Three vertices of a parallelogram (PQRS) P(-1, 2), Q(8, -5) and R(5,0).
    1. On the grid provided draw the parallelogram PQRS. (1 mark)
       Determine the length of diagonal QS. (2 marks)
13. In January, Mambo donated ¹/₆th of his salary to the children’s home while Simba donated ¹/₅ th of his salary to the same children’s home. Their total donation for January was Ksh 14 820. In February, Mambo donated ¹/₈th of his salary to the children’s home while Simba donated ¹/₁₂th of his salary to the children’s home. Their total donation for January was Kshs 8 675. Calculate Mambo’s monthly salary. (4 marks)
14. 1. Express 10500 in terms of its prime factors. (1 mark)
    2. Determine the smallest positive number P such that 10500P is a perfect cube. (2 marks)
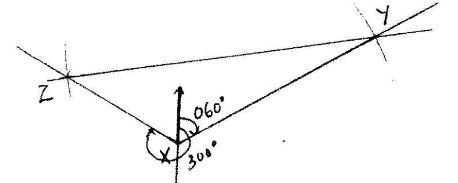
15. Three police posts X, Y and Z are such that Y is 50 km on a bearing of 060⁰ from X while Z 70 km from Y and on a bearing of 300⁰ from X. 
    
    1. Using a suitable scale, draw a diagram to represent the above situation. (3 marks)
    2. Determine the distance, in km, of Z from X. (1 mark)
16. A small cone of height 8 cm is cut off from a bigger cone to leave a frustum of height 16 cm. If the volume of the smaller cone is 160 cm³, find the volume of the frustum. (3 marks)
    

    SECTION II (50 marks)
    
    Answer any five questions from this section in the spaces provided.
    

17. A solid consists of a cone and a hemisphere. The common diameter of the cone and the hemisphere is 12 cm and the slanting height of the cone is 10 cm.
    
    1. Calculate correct to two decimal places.
       1. The surface area of the solid. (3 marks)
       2. The volume of the solid. (4 marks)
    2. If the density of the material used to make the solid is 1.3 g/cm³, calculate its mass in kilograms. (3 marks)
18. Makau made a journey of 700 km partly by train and partly by bus. He started his journey at 8.00 a.m. by train which travelled at 50km/h. After alighting from the train, he took a lunch break of 30 minutes. He then continued his journey by bus which travelled at 75 km/h. The whole journey took 11¹/₂ hours.
    
    1. Determine:
       1. the distance travelled by the bus. (4 marks)
       2. The time Makau started travelling by bus.(3 marks)
    2. The bus developed a puncture after travelling 187 ¹/₂ km. It took 15 minutes to replace the wheel. Find the time taken to complete the remaining part of the journey. (3 marks)
19. 1. The product of matrices (⁰₂ ¹_p)and (^-1.5_p ^-0.5_p-2) is a singular matrix.
       Find the value of p. (3 marks)
    2. A saleswoman earned a fixed salary of Ksh x and a commission of Ksh y for each item sold. In a certain month she sold 30 items and earned a total of Ksh 50000.The following month she sold 40 items and earned a total of Ksh 56000.
       1. Form two equations in x and y. (2 marks)
       2. Solve the equation in (i) above using matrix method. (3 marks)
       3. In the third month she earned Ksh 68000 . Find the number of items sold. (2 marks)
20. In a triangle ABC,BC=8cm,AC=12cm, And angle ABC=120⁰.
    1. Calculate the length AB, correct to one decimal place. (4 marks)
    2. If BC is the base of the triangle ,calculate correct to one decimal place:
       1. The perpendicular height of the triangle: (2 marks)
       2. The area of the triangle; (2 marks)
       3. The area of angle ACB. (2 marks)
21. 1. Using the trapezium rule with seven ordinates, estimate the area of the region bounded by the curve y =-x²+6x+1, the lines x=0,y=0 and x=6.
    2. Calculate:
       1. the area of the region in (a) above integration; (3 marks)
       2. The percentage error of the estimated area to the actual area of the region correct to two decimal places. (2 marks)
22. The displacement, s meters of a moving particle after t seconds are given by:
    s = 2t² - 5t² + 4t + 2.
    Determine;
    1. The velocity of the particle when t=3 seconds: (3 marks)
    2. The value of t when the particle is momentarily at rest; (3 marks)
    3. The displacement when the particle is momentarily at rest; (2 marks)
    4. The acceleration of particle when t=3 seconds. (2 marks)
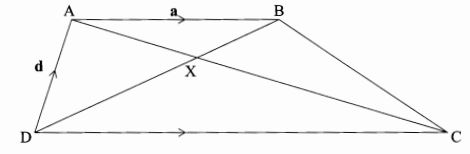
23. In the figure below, ABCD is a trapezium. AB is a parallel to DC, diagonals AC and DB intersect at X and DC=2AB, AB=a, DA=d, AX=kAC and DX= hDB, Where h and k are constants.
    
    
    1. Find the terms of a and d.
       1. BC; (2 marks)
       2. AX; (2 marks)
       3. DX; (1 mark)
    2. Determine the values of h and k. (5 marks)
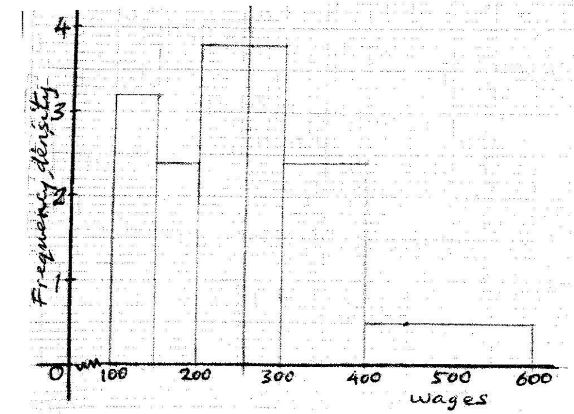
24. The frequency table below shows the daily wages paid to casual workers by a certain company.
    
    1. Draw a histogram to represent the above information. (5 marks)
    2. 
       
       1. State the class in which the median wage lies. (1 mark)
       2. Draw a verticals line, in the histogram, showing where the median wage lies. (1 mark)
    3. Using the histogram, determine the number of workers who can earn sh 450 or less per day. (3 marks)

MARKING SCHEME

1.  2¹/₅ + ²/₃ x ¹⁵/₄ - 4 ¹/₆= ⁸/₁₅
   1 ¹/₄ - ¹²/₅ x ³/₄ + 3 ³/₄ = 3¹/₅
   ⁸/_¹⁵/ 3 ¹/₅ = ¹/₆
   
   
2. √11.25² - 6.75²=9
   perimeter= 2(9+6.75)=31.5
   
   
3. Let d be distance covered
   ^3d/₅ - ^d/₂ = ^d/₁₀
   %change= d/10/d/2 x100%
   = ^d/₁₀ x ²/_d x 100%
   20%
4. 60= 2²x3x5
   42=2x3x7
   side of room= 2²x3 x5x7=420cm
   LEast area=4.2m x 4.2m=17.64m²
   
   
5. Sin(x+60º)=Cos2x
   x+60+2x=90º
   3x=30º
   x=10º
   Tan(x+60º)=tan 70º
   =2.75
   
   
6.   4x-9x3   = x(2-3x)(2+3x)
   3x2-4x-4     (3x+2)(x-2)
   =x(2-3x)
        x-2
7. Internal Dimension: 40, 20 and 15
   Volume occupied = 40 x 20 x 15 - 8000= 4000
   Height above water level = ⁴⁰⁰⁰/_40x20=5cm
   
   
8. 2x²y²-5xy-12=2x²y²-8xy+3xy-12
   =2xy(xy-4)+3(xy-4)
   =(2xy+3)(xy-4)
9.    
   
   Perpendicular distance between PQ and SR=3.9cm
10.   
    

    Mass(kg)x	40-44	45-49	50-54	55-59	60-64	65-69	70-74
    No of people,f	1	2	12	10	2	2	1
    Midpoint of x	42	47	52	57	62	67	72
    fx	42	94	624	570	124	134	72

    
    mean mass, x= Σfx=1660 = 551/3
                            Σx     30 
11.   Selling price before discount = 5880/98 x 100%
    =6000
    Price at which shopkeeper bought the suit= ⁶⁰⁰⁰/₁₂₀ x 100% = 5000
    
    
12.    
    
13. Let Mambo's salary be x and Simba's slary be y
    1/6 x + 1/5y=14820
    1/8x + 1/12y=8675
    5x+6y= 444600
    3x+2y=208200
    5x+6y=444600
    9x+6y=624600
    4x=180000
    x=45000
14.     
    1. 10500=2²x3x5³x7
    2. px10500=2³x3³x5³x7³
       Smallest value of P=2x3²x7²=882
15.    
    
    distance XZ=3 x 10=30km
16. LSF= 8:24=1:3
    VSF=1:27
    Volume of frustrum=160 x 27 - 160
    =4160cm3
17.     
    1.        
       1. π x 6 x 10+ ⁴/₃ x π x 6²=414.49
       2. Height of cone = √100-36=8
          ∴Volume of the solid= ¹/₃ x π x 6² x 8 + ¹/₂ x ⁴/₃ x π x 6³
          =753.98cm³
    2. Mass of solid in kg = 1.3 x 753.98 =0.98kg
                                           1000
18.         
    1.      
       1. Let distance covered by bus be b km
          ∴time by train = ^700-b/₅₀
          time by bus = ^b/₇₅
          ∴^700-b/₅₀ + ^b/₇₅=11 ¹/₂ - ¹/₂
          2100-3b+2b=11
             150
          2100 - b=11x150
          b=2100-1650=450
          
          
       2. Time taken by train= ^700-450/₅₀ = 5h
          total time before departure of bus = 5h+30min
19.        
    1.       
       
       -p+p3-2p2=p3-2p2-3p+6
       -p=-3p+6
       p=3
    2.         
       1. x+30y=50000
          x+40y=56000
       2.    
          
          x=32000
          y=600
       3. 68000-32000=60
              600
20.     
    
21.       
    1. ordinates
       x=0 y1=1
       x=1 y2=6
       x=2 y3=9
       x=3 y4=10
       x=4 y5=9
       x=5 y6=6
       x=6 y7=1
       Area= 1/2 x 1 x {1+1+2(6+9+10+9+6)}=1/2(82)=41
       
       
    2.    
       1. ₀∫⁶ - x² + 6x+1=[-¹/₃x³+⁶/₂x²+x]⁶₀ =-72+108+6=42
       2. ^42-41/₄₂ x 100%=2.38%
22.            
    1. V=^ds/_dt=6t²-10t+4
       When t=3
       v=6(9)-10(3)+4=28m/s
       
       
    2. v=0→6t²-10t+4=0
       3t²-5t+2=0
       (3t-2)(t-1)=0
       t=²/₃ or t=1
       
       
    3. t=²/₃: s=2(²/₃)³-5(²/₃)²+4(²/₃)+2=3.04
       t=1, s=(1)³-5(1)²+4(1)+2=3m
       
       
    4. a=^dv/_dt=12t-10
       t=3:a=12(3)-10=26
23.         
    1.     
       1. BC=BD+DC
          =-d-a+2a
          =a-d
       2. AX=kAC→AX=k(2a-d)
       3. DX=hDB→DX=h(d+a)
    2. AX=-d+hd+ha
       AX=d(h-1)+ha
       AX=2ka-kd
       ∴d(h-1)+ha=2ka-kd
       h=2k and h-1=-k
       h=-k+1  2k=-k+1
       3k=1
       k=¹/₃
       h=2k→h=2x¹/₃=²/₃
24.        
    1.    
       
    2. Median class: 200-300
    3. Number of workers who earn Sh.450 or less per day= 900+50x0.5=925