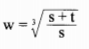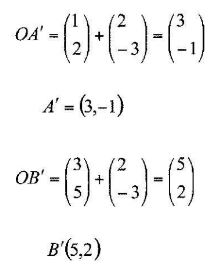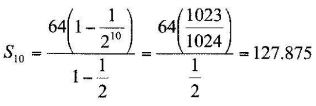KCSE 2011 Mathematics Paper 2 with Marking Scheme

Section 1(50 marks)
Answer all the questions in this section in the spaces provided.

1. Use logarithms, correct to 4 decimal places, to evaluate. (4 marks)
   
2. Three grades A,B and C of rice were mixed in the ratio 3:4:5. The cost per kg of each of the grades A,B and C were Ksh 120, Ksh 90 and Ksh 60 respectively.
   Calculate:
   1. The cost of one kg of the mixture; (2 marks)
   2. The selling price of 5 kg of the mixture given that the mixture was sold at 8% profit. (2 marks)
3. Make s the subject of the formula.
   
4. 1. Solve the inequalities 2x-5 > -11 and 3+2x ≤ 13, giving the answer as a combined inequality. (3 marks)
   2. List the integral values of x that satisfy the combined inequality in (a) above. (1 marks)
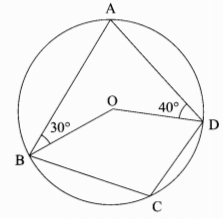
5. In the figure below, ABCD is a cyclic quadrilateral, point O is the center of the circle. Angle ABO=30° and angle ADO=40°
   
   Calculate the size of angle BCD. (2 marks)
6. The ages in years of five boys are 7,8,9,10 and 11 while those of five girls are 4,5,6,7 and 8. A boy and a girl are picked at random and the sum of their ages recorded.
   1. Draw a probability space to show all the possible outcomes. (1 mark)
   2. Find the probability that the sum of their ages is at least 17 years. (1 mark)
7. The vertices of a triangle are A(1,2),B(3,5) and C(4,1). The coordinates of C’ the image of C under a translation vector 1, are (6,-2).
   1. Determine the translation vector T. (1 mark)
   2. Find the coordinates of A’ and B’ under translation vector T. (2 marks)
8. Write sin 45⁰ in the form ¹/_√a where a is a positive integer .Hence simplify . Leaving the answer in surd form. (3 marks)
9. The radius of a spherical ball is measured as 7 cm , correct to the nearest centimeter. Determine, to 2 decimal places , the percentage error in calculating the surface area of the ball. (4 marks)
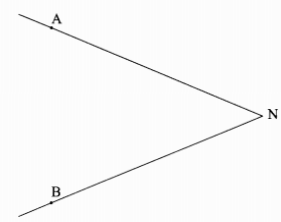
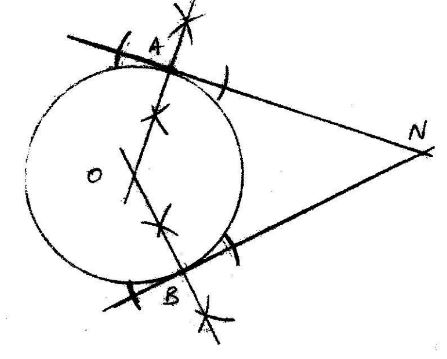
10. 1. In the figure below , lines NA and NB represent tangents to a circle at points A and B. Use a pair of compasses and ruler only to construct the circle. (2 marks)
       
       
    2. Measure the radius of the circle. (1 mark)
11. Expand and simplify the expression. (a+1⁄2)⁴ + (a-1⁄2)⁴ (3 marks)
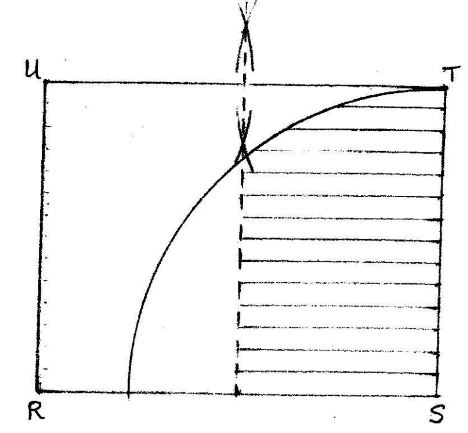
12. The figure below represents a scale drawing of a rectangular piece of land ,RSTU. RS=9cm and ST=7cm.
    
    An electric post P, is to be erected inside the piece of land . On the scale drawing, shade the possible region in which P would lie such that PU=PT and PS ≤ 7cm. (3 marks)
13. Vector OP=6i + j and OQ=-2i + 5j. A point N divides PQ internally in the ratio 3:1 Find PN in terms of i and j. (3 marks)
14. A point M (60⁰N,18⁰E) is on the surface of the earth. Another point N is situated at a distance of 630 nautical miles east of M.
    Find:
    1. the longitude difference between M an N; (2 marks)
    2. The position of N. (1 mark)
15. The equation of a circle center (a,b) is x² + y² - 6x - 10y + 30 = 0. Find value of a and b. (3 marks)
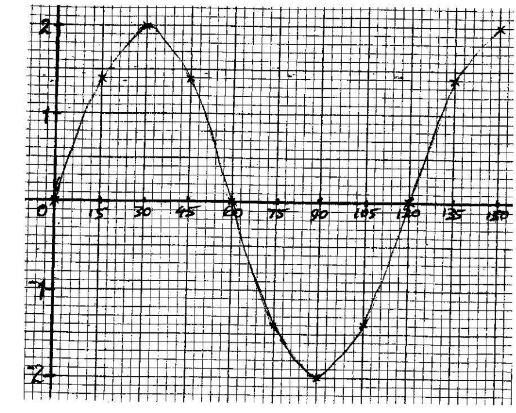
16. The table below shows values x and y for the function y = sin 3x⁰ in the range 0⁰ ≤ x ≤ 150°.
    
    
    1. On the grid provided, draw the graph of y = 2 sin 3x. (2 marks)
    2. From the graph determine the period. (1 mark)

    SECTION II (50 marks)
    Answer only five questions in this section in the spaces provided.
    
    

17. The cash price of a laptop was ksh 60000. On hire purchase terms, a deposit if ksh 7500 was paid followed by 11 monthly installments of ksh 6000 each.
    1. Calculate;
       1. The cost of a laptop in a hire purchase terms; (2 marks)
       2. The percentage increase of hire purchase price compared to the cash price. (2 marks)
    2. An institution was offered a 5% discount when purchasing 25 such laptops on each terms. Calculate the amount of money paid by the institution. (2 marks)
    3. Two other institutions X and Y bought 25 laptops each. Institution X bought the laptops on hire purchase terms. Institution Y bought the laptops on cash terms with no discount by securing a loan from a bank. The bank charged 12% p.a compound interest for two years.
       Calculate how much more money institution Y paid than institution X. (4 marks)
18. The first, fifth and seventh terms of an arithmetic Progression (AP) correspond to the first three consecutive terms of a decreasing Geometric Progression (GP).The first term of each progression is 64, the common difference of AP is d and the common ratio of the G.P is r.
    
    1. 1. Write two equations involving d and r. (2 marks)
       2. Find the values of d and r. (4 marks)
    2. Find the sum of the first 10 terms of
       1. The arithmetic Progression.(AP); (2 marks)
       2. The Geometric Progression (GP). (2 marks)
19. The vertices of a rectangle are A(-1,-1), B(-4.-1),C(-4,-3) and D(-1,-3).
    1. On the grid provided, draw the rectangle and its image A’B’C’D’ under a transformation whose matrix is (^-2₀ ⁰_-2). (4 marks)
       
    2. A’’B’’C’’D’’ is the image of A’B’C’D’ under a transformation matrix
       P = (1/21 11/2)
       
       1. Determine the coordinates of A’’,B’’,C’’ and D’’. (2 marks)
       2. On the same grid draw the quadrilateral A’’B’’C’’D’’. (1 mark)
    3. Find the area of A’’B’’C’’D’’. (3 marks)
20. A parent has two children whose age difference is 5 years. Twice the sum of the ages of the two children is equal to the age of the parent.
    1. Taking x to be the age of the elder child , write an expression for,
       1. The age of the younger child; (1 mark)
       2. The age of the parent. (1 mark)
    2. In twenty years time, the product of the children’s ages will be 15 times the age of their parent. (2 mark)
       1. Form an equation in x and hence determine the present possible ages of the elder child. (4 marks)
       2. Find the present possible ages of the parent. (2 marks)
    3. Determine the possible ages of the younger child in 20 years time. (2 marks)
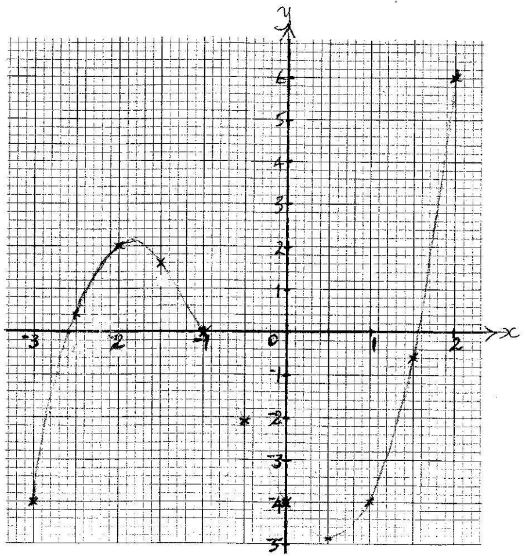
21. The table below shows values of x and some values of y for the curve y = x³ + 2x² - 3x - 4 for -3≤ x ≤2.
    
    
    1. Complete the table by filling in the missing values y, correct to 1 decimal place. (2 marks)
    2. On the grid provided, draw the graph of y = x³ + 2x² - 3x - 4.
       Use the scale: 1cm represents 0.5 units on x-axis.
       1 cm represents 1 unit in y-axis. (3 marks)
    3. Use the graph to:
       1. Solve the equation x³ + 2x² - 3x - 4 = 6; (3 marks)
       2. Estimate the coordinates of the turning points of the curve. ( 2 marks)
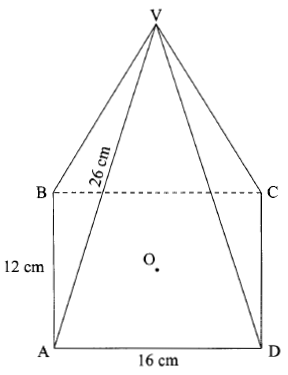
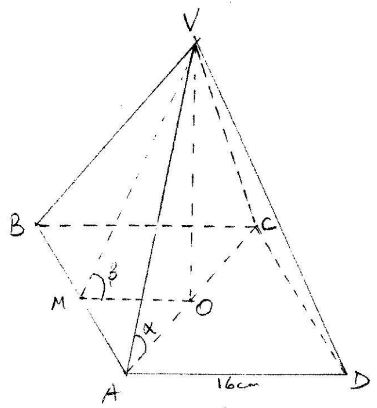
22. The figure below represents a rectangular based pyramid VABCD. AB = 12 cm and AD = 16cm. Point O is vertically below V and VA =26 cm.
    
    Calculate;
    1. The height,VO, of the pyramid. (4 marks)
    2. The angle between the edge VA and the plane ABCD; (3 marks)
    3. The angle between the planes VAB and ABCD.(3 marks)
23. The cost C, of producing n items varies partly as n and partly as the inverse of n . To produce two items it costs ksh 135 and to produce three items it cost ksh 140.
    Find:
    1. The constants of proportionality and hence write the equation connecting C and n; (5 marks)
    2. The cost of producing 10 items; (2 marks)
    3. The number of item produced at a cost of ksh 756. (3 marks)
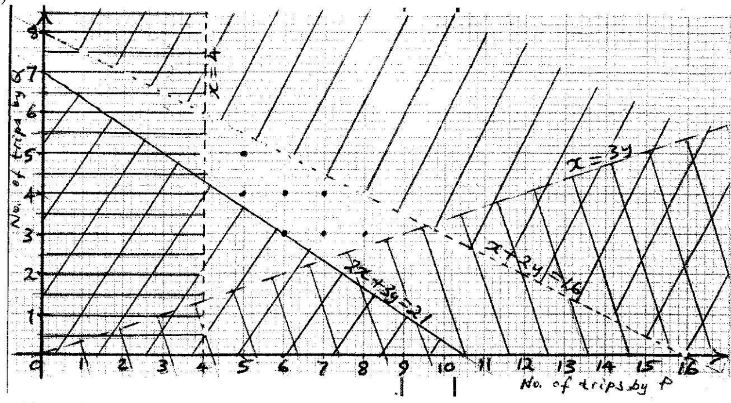
24. A building contractor has two lorries, P and Q used to transport at least 42 tonnes of sand to a building site. Lorry P carries 4 tonnes of sand per trip while lorry Q carries 6 tonnes of sand per trip. Lorry P uses 2 litres of fuel per trip while lorry Q uses 4 litres of fuel per trip. The two lorries are to use less than 32 litres of fuel. The number of trips made by lorry P should be less than 3 times the number of trips made by lorry Q .Lorry P should make more than 4 trips.
    1. Taking x to represent the number of trips made by lorry P and y to represent the number of trips made by lorry Q, write the inequalities that represent the above information. (4 marks)
    2. On the grid provided, draw the inequalities and shade the unwanted regions. (4 marks)
    3. Use the graph drawn in (b) above to determine the number of trips made by lorry P and by lorry Q to deliver the greatest amount of sand. (2 marks)

MARKING SCHEME

1.   
   

   No	Log
   83.46 0.0054 1.562	1.9215 + 3.7324 1.6539 - 0.3862 1.2677 ÷ 3
   0.5700	1.7559

2.     
   1. cost of 1kg of mixture
      =120 x 3 + 90 x 4 + 6 x 5
                    12
      =85
   2. Cost of 5kg of mixture
      =¹⁰⁸/₁₀₀ x 85 x 5
      =459
3. w³= ^s+t/₂
   w³s=s+t
   w³s-s=t
   s=^t/_w³-1
4.     
   1. 2x-5>-11→2x>-6→X>-3
      3+2X<13→2X<10→x<5
      ∴-3<x<5
   2. Integral values: -2, -2, 0, 1, 2, 3, 4, 5
5.        
6.        
   1.  
      

      +	7	8	9	10	11
      4	11	12	13	14	15
      5	12	13	14	15	16
      6	13	14	15	16	17
      7	14	15	16	17	18
      8	15	16	17	18	19

          
   2.  P(sum of at least 17)=6/25
7.         
   1.    
      
   2.   
      
8. sin 45°= 1/√2
       √8        = 2√2(1-1/√2)        
   1+Sin 45       (1+¹/_√2) (1-¹/_√2)
   = 2√2-2
         ¹/₂
   =4(√2-1)
   
   
9. Maximum area= 4π x 7.5²
   Minimum area= 4π x 6.5²
   Absolute error= 4π (7.5² - 6.5²)/2
   =28π
   %error=    28π     x 100%
                  4πx7x7
   =14.29%
10.    
    
11. (a+¹/₂)⁴+(a-¹/₂)⁴=[a⁴+4a⁴(¹/₂)+6a²(¹/₂)²+4a(¹/₂)³+(¹/₂)⁴]-
    [a⁴+4a³(-¹/₂)+6a²(-¹/₂)²+4a(-¹/₂)³+(-¹/₂)⁴]
    =2a⁴+3a²+¹/₈
12.    
    
13. PQ=-6i-j-2i+5j=-8i+4j
    PN=3/4(-8i+4j)=-6i+3j
14.     
    1. let longitude difference be θº
       θx60Cos60º=630
       θ= ⁶³⁰/_60Cos60º
       21º
    2. 21º due east of 18ºE is the longitude (18º+21º)E
       Location of N is (60ºN, 39ºE)
15. x²+y²-6x-10y+30=0
    x²-6x+9+y²-10y+25=4
    (x-3)²+(y-5)²=2²
    a=3, b=5
16.   
    
    Period= 120°
17.    
    1.      
       1. 7500 + 11 x 6000=73500
       2. 73500 - 60000 x 100=22.5%
               60000
    2. 60000 x 25 x 0.95=1425000
    3. institution X
       73500 x 25=1837500
       Institution Y
       60000 x 25 x (1.12)²=1881600
       Difference = 1881600 - 1837500=44100
18.          
    1.         
       1. 64+4d=64r
          64+6d=64r2
       2. From (i)
          d=16r-16
          64r2=64+6(16r-16)
          64r2=64+96r-96
          2r2-3r+1=0
          (2r-1)(r-1)=0
          r=1/2 or r=1
          For decreasing GP, r=1/2
          Substituting r = 1/2 in (i)
          64x1/2= 64+4d
          d=-8
    2.        
       1. A.P
          S10=10/2{2x64+9x-8}=280
       2. G.P
          
19.            
    1.  
          
    2.    
       
       coordinates A'(3,3)B"(6,9)C"(10,11)D"(7,5)
    3. Determinant of matrix P= ¹/₂ x ¹/₂ -1 x 1
       =-³/₄
       Area of A"B"C"D"=³/₄x6x4=18sq units
20.          
    1.     
       1. x-5
       2. [x+(x-5)]x2=4x-10
    2.         
       1. (x=20)(x+15)=15(4x+10)
          x²-25x+150=0
          (x-10)(x-15)=0
          x=10 or x=15
       2. Parent's possible ages
          4x10-10=30
          or 4 x15 -10=50
       3. Possible ages of younger child in 20 years time
          (10-5)+20=25
          or(15-5)+20=30
21.        
    1.      
       1.     
          

          x	-3	-2.5	-2	-1.5	-1	-0.5	0	0.5	1	1.5	2
          y=x3+2x2-3x-4			2			-2.1				-4-0.6

       2.    
          
    2.         
       1. x=-2.6, -1, 1.55
       2. Coordinates of turning points
          (-1.85, 2.1) and (0.5, 4.9)
22.      
         
    1. Height VO
       AC2=162+122=400
       AC=20
       AO=20÷2=10
       VO=√26²-10²=24
       
       
    2. Angle between edge VA and Plane ABCD=angle VAO=α
       ^h/₁₀ = tan α
       α=tan^-1 2.4
       =67.38º
    3. Angle between planes VAB and ABCD=angle VMO=β
       ^h/₈=tanβ
       β=tan^-1 3
       =71.57°
23.           
    1. c=an+b/n
       135=2a+b/2
       140=2a+b/3
       270=4a+b
       420=9a+b
       150=5a→a=30
       270=120+b→b=150
       c=30n+150/n
       
       
    2. c=30x10+150/10
       =315
       
       
    3. 756=30n+150/n
       756n=30n2+150
       5n2-126n+25=0
       (5n-1)(n-25)=0
       n=1/5 or n=25
       number of items = 25
24.          
    1. 4x+6y>42→2x+3y>21
       2x+4y<32→x+y<16
       x<3y
       x>4
    2.    
       
    3. x=5, y=5→ 5 x 4 + 5x6=50 tons
       x=6, y=4 → 6x4+4x4x6=48tons
       x=7, y=4→ 7x4+4x6=52 tons
       7 trips by P and 4 trips by Q