INSTRUCTIONS TO CANDIDATES
- The paper contains two sections: Section I and II
- Answer ALL questions in section I and ONLY FIVE questions from section II.
- All working and answers must be written on the question paper in the spaces provided below each question.
- Marks may be awarded for correct working even if the answer is wrong.
- Negligence and slovenly work will be penalized.
- Non-programmable silent electronic calculators and mathematical tables are allowed for use.
FOR EXAMINER’S USE ONLY
SECTION 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
TOTAL |
SECTION II
|
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
TOTAL |

QUESTIONS
- Without using a calculator, evaluate (3mks)
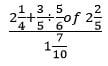
- A number n is such that when it is divided by 3,7,11 or 13, the remainder is always one. Find the number n (2mks)
- Solve the inequality
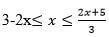 and show the solution on the number line (3mks)
and show the solution on the number line (3mks) - In the figure below AB is parallel to DE and area of triangle DEC is 8cm2.
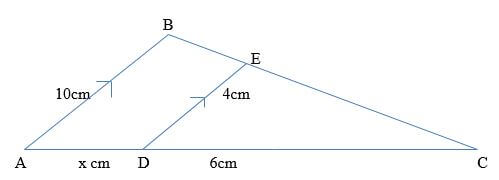
Find- The value of x (2mks)
- The area of quadrilateral ABED (2mks)
- A bank in Kenya buys and sells foreign currencies as follows;
A tourist arrived in Kenya with US dollar 3500. He converted all the dollars to Kenya shillings at the bank. While in Kenya, he spent Ksh115,000 and then converted the remaining amount to sterling Pounds. Calculate the amount he received in Sterling pounds (3mks)Currency
Buying(Ksh)
Selling (Ksh)
1 sterling Pound
1 US dollar
132.40
70.40
132.75
70.84
- Solve for x given that; (2mks)
Cos(2x – 40)° = sin (-20 +3x)° - The size of an interior angle of a regular polygon is 3x° while its exterior angle is (x-20)°. Find the number of sides of the polygon. (3mks)
- Log 5 -2 +log (2x+10) = log (x-4) (3 mks)
- Find the equation of the perpendicular bisector of a straight line passing through the points P(2,7) and Q(4,3) giving your answer in the form ax +by +c =0 (4mks)
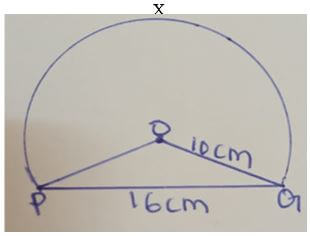
- The figure below shows a sector of a circle with centre O, radius 10cm. The chord PQ=16cm Calculate the area of the sector PXQ (4mks)
- Simplify the expression (3mks)
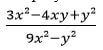
- Use the reciprocal tables to evaluate (3mks)
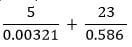
- The volumes of two similar solid cylinders are 4752cm3 and 1408cm3. If the area of the curved surface of the smaller cylinder is 352cm2, find the area of the curved surface of the larger cylinder (4mks)
- A bus takes 195 minutes to travel a distance of (2x +30) km at an average speed of (x-20)km/h. Calculate the actual distance travelled. Give your answer in kilometres (3mks)
- Given that OA =3i -2j and OB=4i+j. Find the distance between points A and B correct to 1 decimal place (2mks)
- Murimi and Naliaka had each 288 tree seedlings.Murimi planted equal number of seedlings per row in x rows while Naliaka planted equal number of seedlings in (x+1) rows. The number of tree seedlings planted by Murimi in each row were 4 more than those planted by Naliaka in each row. Calculate the number of seedling Murimi planted in each row. (4 mks)
SECTION II.(ANSWER FIVE QUESTIONS ONLY
- Two business partners Mary and John contributed Ksh.60000 and Ksh90000 respectively to start up a business. After 6 months, Lucy joined the business partnership and contributed Ksh.100000. At the end of the year, a gross profit of Ksh.720000 was realized. They then agreed to re-invest 30% of the profit accrued back into the business and use 20% of the profit for running the business operations. The remainder was to be shared among the business partners in the ratio of their contribution.
- Calculate the amount;
- Re-invested into the business (2mks)
- Used for business operations (1mk)
- Calculate the amount of profit each partner got (4mks)
- If the amount put back into the business was added to individual’s shares proportional to their initial contribution, find the amount of each partner’s shares (3mks)
- Calculate the amount;
- A bus left Nairobi at 7.00a.m and travelled towards Eldoret at an average speed of 80km/h. At 7.45a.m a car left Eldoret towards Nairobi at an average speed of 120km/h. Given that the distance between Nairobi and Eldoret is 300km. Calculate;
- The time the bus arrived at Eldoret (2mks)
- The time of the day, the two met (3mks)
- The distance from Nairobi where the two met (2mks)
- The distance of the bus from Eldoret when the car arrived in Nairobi (3 mks)
- The figure below shows a solid which is a rectangular based pyramid of height 12cm.
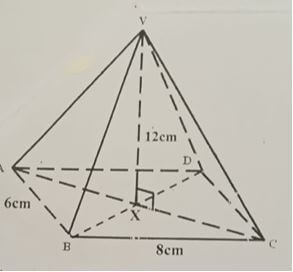
- Calculate the slanting length VC (2mks)
- Calculate the surface area of the pyramid (4mks)
- Calculate the volume of the pyramid (2mks)
- Determine the density of the metal which make this solid if its mass is 1.632kg (2mks)
- In the figure below OJKL is a parallelogram in which OJ = 3p ̃ and OL = 2 r
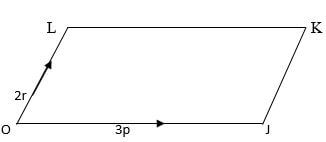 ̃
̃- If A is a point on LK such that LA = ½ AK and point B divide the line JK externally in the ratio 3:1, express OB and AJ in terms of p and r. (2 marks)
- Line OB interests AJ at X such that OX = mOB and AX = nAJ.
- Express OX in terms of p, r and m. (1 mark)
- Express OX in terms of p, r and n (1 mark)
- Determine the value of m and n and hence the ratio in which point x divides line AJ. (6 marks)
- The figure below shows two triangles, ABC and BCD with a common base BC=3.4cm, AC=7.2cm, CD=7.5cm and <ABC=90°. The area of triangle ABC=Area of triangle BCD.
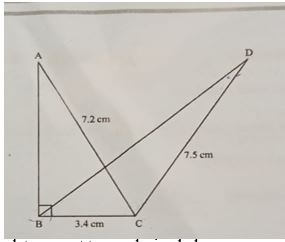
Calculate correct to one decimal place;- The area of triangle ABC (3mks)
- The size of <BCD (3mks)
- The length of BD (2mks)
- The size of <BDC (2mks)
- The equation of a curve is y=x3+4x2 -3.
- Fill in the table below for the curve y=x3+4x2 – 3 (2mks)
x
-4
-3
-2
-1
0
1
y
- On the grid provided, draw the curve y=x3+4x2 - 3 for the range -4≤x≤1 scale: Horizontal axis 2cm represent 1 unit vertical axis 1cm rep 1 unit (3mks)

- Use your graph to solve
- x3 +4x2 – 3 = 0 (2mks)
- 4x3 +16x2 –x – 16 = 0 (3mks)
- Fill in the table below for the curve y=x3+4x2 – 3 (2mks)
-
- A straight line L1 whose equation is y-2x=4 meets the x-axis at M. Determine co-ordinates of M. (1mk)
- A second line L2 is perpendicular to L1 at M. Find the equation of Line L2 in the form ax+by+c=0 where a,b and c are integers. (3mks)
- A third line L3 passes through (2,3) and is parallel to L1. Find;
- The equation of L3 in the form y=mx +c (3mks)
- Point N, the intersection of L2 and L3 (3mks)
- A curve is represented by the function y=x3 +x2 – x
- Find dy/dx (1mk)
- Determine the values of y at the turning points of the curve y =x3 +x2 –x (4mks)
- Determine the nature of the turning points (2mks)
- In the space provided below, sketch the curve of y=x3+x2 –x (3mks)

MARKING SCHEME
- Without using a calculator, evaluate (3mks)
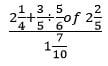
9/4 + 3/10 = 45 + 6
20
= 51 x 10
20 17
= 3/2
11/2 - A number n is such that when it is divided by 3,7,11 or 13, the remainder is always one. Find the number n (2mks)
3, 7 , 11, 13
lcm = 3 x 7 x 1 x 13
= 3003
number = 3003 + 1
= 3004 - Solve the inequality
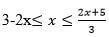 and show the solution on the number line (3mks)
and show the solution on the number line (3mks)
3 - 2x ≤ x
-3x ≤ -3
x ≥ -1
x ≤ 2x + 5
3
3x ≤ 2x + 5
x ≤ 5
- In the figure below AB is parallel to DE and area of triangle DEC is 8cm2.

Find- The value of x (2mks)
4/10 = 6/6 + x
24 + 4x = 60
4x = 36
x = 9 - The area of quadrilateral ABED (2mks)
8 = 4 (A.SF)
Area of Δ ABC 25
Area of Δ ABC = 8 x 25 = 50cm2
4
Area of quadrilateral = 50 - 8
= 42 cm2
- The value of x (2mks)
- A bank in Kenya buys and sells foreign currencies as follows;
A tourist arrived in Kenya with US dollar 3500. He converted all the dollars to Kenya shillings at the bank. While in Kenya, he spent Ksh115,000 and then converted the remaining amount to sterling Pounds. Calculate the amount he received in Sterling pounds (3mks)Currency
Buying(Ksh)
Selling (Ksh)
1 sterling Pound
1 US dollar
132.40
70.40
132.75
70.84
3500 x 70.40 = 246, 400 ksh
246 400 - 115 000 = ksh 131 400
= 131 400
132.75
= 989.83 pounds - Solve for x given that; (2mks)
Cos(2x – 40)° = sin (-20 +3x)°
(2x - 40) + (-20 + 3x) = 90
2x - 40 - 20 + 3x = 90
5x = 150
x = 30º - The size of an interior angle of a regular polygon is 3x° while its exterior angle is (x-20)°. Find the number of sides of the polygon. (3mks)
3x + (x - 20) = 180
4x = 20º
x = 50
exterior angle = 50 - 20 = 30º
number of sides = 360
30
= 12 sides - Log 5 -2 +log (2x+10) = log (x-4) (3 mks)
ans
= x = 5 - Find the equation of the perpendicular bisector of a straight line passing through the points P(2,7) and Q(4,3) giving your answer in the form ax +by +c =0 (4mks)
g1 = 7 - 3 = 4 = -2
2 - 4 -2
g2 = 1/2
midpoint =( 2 + 4 7 + 3)
2 2
= (3, 5)
y - 7 = 1
x - 2 2
x - 2 = 2y - 14
x - 2y + 12 = 0 - The figure below shows a sector of a circle with centre O, radius 10cm. The chord PQ=16cm Calculate the area of the sector PXQ (4mks)

sin 1/2x = 8/10
sin 1/2 = 0.8
1/2x = 53.13
x = 106.26
sector area = (360 - 106.26) x 22 x 102
360
= 2253.74 x 22 x 100
360 7
= 221.52 - Simplify the expression (3mks)
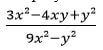
num = 3x2 - 4xy + y2
3x2 - 3xy - xy + y2
3x (x - y) - y(x - y)
(3x - y)(x - y)
den = 9x2 - y2
= (3x - y)(3x - y)
num = (3x - y) (x - y)
den (3x - y) (3x - y)
= x - y
3x - y - Use the reciprocal tables to evaluate (3mks)
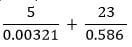
(3.21 x 10-3)-1 = 0.3115 x 103
= 311.5
(5.86 x 10-1)-1 = 0.1706 x 10
= 1.706
=(5 x 311.5) + 23(1.906)
=1557.5 + 39.238
= 1596.738 - The volumes of two similar solid cylinders are 4752cm3 and 1408cm3. If the area of the curved surface of the smaller cylinder is 352cm2, find the area of the curved surface of the larger cylinder (4mks)
v.s.f = 4752/1408 = 3.375
l.s.f = (3.375)1/3 = 1.5
a.s.f = 1.62 = 2.25
area of larger cylinder = 2.25 x 352
= 792 cm2 - A bus takes 195 minutes to travel a distance of (2x +30) km at an average speed of (x-20)km/h. Calculate the actual distance travelled. Give your answer in kilometres (3mks)
195 min = 13/4 hr
13/4 = 2x + 30
x - 20
13x - 260 = 8x + 120
5x = 380
x = 76 km
distsance = 2x + 30
=2(76) + 30
= 182 - Given that OA =3i -2j and OB=4i+j. Find the distance between points A and B correct to 1 decimal place (2mks)
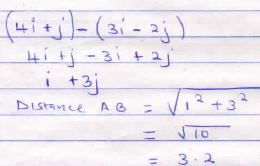
- Murimi and Naliaka had each 288 tree seedlings.Murimi planted equal number of seedlings per row in x rows while Naliaka planted equal number of seedlings in (x+1) rows. The number of tree seedlings planted by Murimi in each row were 4 more than those planted by Naliaka in each row. Calculate the number of seedling Murimi planted in each row. (4 mks)
288 - 288 = 4
x x + 1
288 (x - 1) - 288x = 4
x(x + 1)
288x + 288 - 288x = 4x(x + 1)
288 = 4x2 + 4x
x2 + x - 72 = 0
x2 + 9x - 8x - 72 = 0
x(x + 9) - 8(x + 9) = 0
(x - 8)(x + 9) = 0
x = 8 or -9 hence
x = 9
SECTION II.(ANSWER FIVE QUESTIONS ONLY
- Two business partners Mary and John contributed Ksh.60000 and Ksh90000 respectively to start up a business. After 6 months, Lucy joined the business partnership and contributed Ksh.100000. At the end of the year, a gross profit of Ksh.720000 was realized. They then agreed to re-invest 30% of the profit accrued back into the business and use 20% of the profit for running the business operations. The remainder was to be shared among the business partners in the ratio of their contribution.
- Calculate the amount;
- Re-invested into the business (2mks)
0.3 x 720, 000 = 216 000 - Used for business operations (1mk)
0.2 x 720,000 = 144,000
- Re-invested into the business (2mks)
- Calculate the amount of profit each partner got (4mks)
60,000 x 1 : 90,000 x 1 : 100,000 x 0.5
60 : 90 : 50
6 : 9 : 5
720, 000 - (216 000 + 144,000) = 360,000
6/20 x 360000 = 108,000
9/20 x 360000 = 160000
5/20 x 360000 = 90000 - If the amount put back into the business was added to individual’s shares proportional to their initial contribution, find the amount of each partner’s shares (3mks)
60000 + 6/20 x 216000 = 124,800
90,000 + 9/20 x 216,000 = 187,200
100,000 + 5/20 x 216,000 = 154,000
- Calculate the amount;
- A bus left Nairobi at 7.00a.m and travelled towards Eldoret at an average speed of 80km/h. At 7.45a.m a car left Eldoret towards Nairobi at an average speed of 120km/h. Given that the distance between Nairobi and Eldoret is 300km. Calculate;
- The time the bus arrived at Eldoret (2mks)
time taken = 300
80
= 3 hr 45 min
7.00 + 3.45 = 10.45 am - The time of the day, the two met (3mks)
distance covered by the bus at 7.45 am = 80 x 3/4 = 60 km
remaining distance = 300 - 60 = 240km
time taken to meet = 240/200
= 1 hr 12 min
time = 7.45 + 1.12
= 8.57 am - The distance from Nairobi where the two met (2mks)
60 km + (80 x 1.2)
60 + 96 = 156 km - The distance of the bus from Eldoret when the car arrived in Nairobi (3 mks)
time taken by the car to reach
Nairobi = 300 = 21/2
120
Distance of bus from nairobi =
60 + (80 x 2.5) = 260 km
distance from Eldoret = 300 - 260
= 40 km
- The time the bus arrived at Eldoret (2mks)
- The figure below shows a solid which is a rectangular based pyramid of height 12cm.

- Calculate the slanting length VC (2mks)

- Calculate the surface area of the pyramid (4mks)
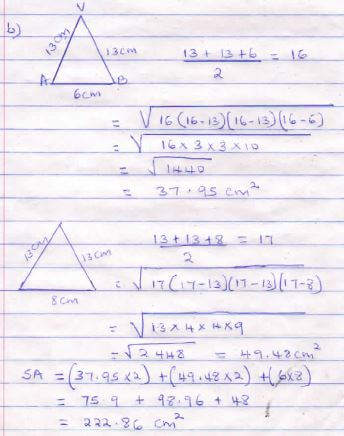
- Calculate the volume of the pyramid (2mks)
volume = 1/3 BA x H
1/3 x 48 x 13
= 192 cm3 - Determine the density of the metal which make this solid if its mass is 1.632kg (2mks)
density = m/v
= 1.632 x 1000
= 1632 g
D = 1632/192
= 8.5 g/cm3 or 8500 kg/m3
- Calculate the slanting length VC (2mks)
- In the figure below OJKL is a parallelogram in which OJ = 3p ̃ and OL = 2 r
 ̃
̃- If A is a point on LK such that LA = ½ AK and point B divide the line JK externally in the ratio 3:1, express OB and AJ in terms of p and r. (2 marks)
OB = 3P +3r
AJ = 2P - 2r - Line OB interests AJ at X such that OX = mOB and AX = nAJ.
- Express OX in terms of p, r and m. (1 mark)
OX = m(OB) = m(3p + 3r)
=3mp + 3mr - Express OX in terms of p, r and n (1 mark)
OX = 2r + p + n(2p - 2r)
= (1 + 2n)p + (2 - 2n)r - Determine the value of m and n and hence the ratio in which point x divides line AJ. (6 marks)
3mp + 3mr = (1 + 2n)p + (2 - 2n)r
3m = 1 + 2n .... (i)
3m = 2 - 2n .....(ii)
1 + 2n = 2 - 2n
4n = 1
n = 1/4
substituting n = 1/4 in eqn (i)
3m = 1 + 2(1/4)
3m = 1 + 1/2
3m = 3/2
m = 1/2
the ratio in which x divides AJ
AX = nAJ = 1/4 AJ
Ratio 1:3
- Express OX in terms of p, r and m. (1 mark)
- If A is a point on LK such that LA = ½ AK and point B divide the line JK externally in the ratio 3:1, express OB and AJ in terms of p and r. (2 marks)
- The figure below shows two triangles, ABC and BCD with a common base BC=3.4cm, AC=7.2cm, CD=7.5cm and <ABC=90°. The area of triangle ABC=Area of triangle BCD.

Calculate correct to one decimal place;- The area of triangle ABC (3mks)
AB = √7.22 - 3.42
= 6.3 x 67
A = 1/2 x 3.4 x 6.3467
= 10.789
=10.8 1 d.p - The size of <BCD (3mks)
area of traingle ABC = Area of triangle BCD
10.8 = 1/2 x 3.4 x 7.5 sin θ
10.8 = 12.75 sin θ
sin θ = 10.8/12.75 = 0.84705
θ = 57.9 acute angle
obtuse angle = 180 - 57.9
= 122.1 1 d.p - The length of BD (2mks)
a2 = b2 + c2 - 2bc cos A
a2 = 3.42 + 7.52 - 2 x 3.4 x 7.5 cos 122.1
a2 = 94.91
a = 9.742 = 9.7 )1 d.p) - The size of <BDC (2mks)
3.4 = 9.7
sinθ sin 122.1
sin θ = 3.4 x sin 122.1 = 0.2969
9.7
θ = 17.273
= 17.3 1 d.p
- The area of triangle ABC (3mks)
- The equation of a curve is y=x3+4x2 -3.
- Fill in the table below for the curve y=x3+4x2 – 3 (2mks)
x
-4
-3
-2
-1
0
1
y
-3 6 5 0 -3 2 - On the grid provided, draw the curve y=x3+4x2 - 3 for the range -4≤x≤1 scale: Horizontal axis 2cm represent 1 unit vertical axis 1cm rep 1 unit (3mks)
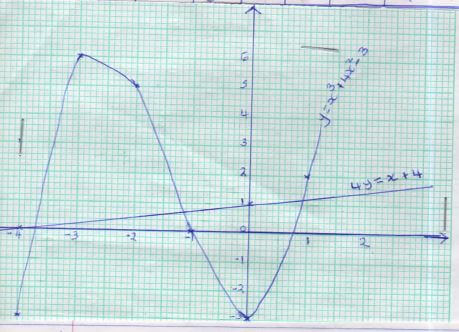
- Use your graph to solve
- x3 +4x2 – 3 = 0 (2mks)
ans = x3 = 0.8 ± 0.05 - 4x3 +16x2 –x – 16 = 0 (3mks)
x3 = 0.95 ± 0.05
- x3 +4x2 – 3 = 0 (2mks)
- Fill in the table below for the curve y=x3+4x2 – 3 (2mks)
-
- A straight line L1 whose equation is y-2x=4 meets the x-axis at M. Determine co-ordinates of M. (1mk)
y - 2x = 4
0 - 2x = 4
-2x = 4
x = -2
(-2, 0) - A second line L2 is perpendicular to L1 at M. Find the equation of Line L2 in the form ax+by+c=0 where a,b and c are integers. (3mks)
m1 x m2 = -1
m1 = 2
m2 = -1/2
y - 0 = -1/2
x + 2
-2y = x + 2
-x - 2y - 2 = 0
x + 2y + 2 = 0 - A third line L3 passes through (2,3) and is parallel to L1. Find;
- The equation of L3 in the form y=mx +c (3mks)
ans
y = 2x - 1 - Point N, the intersection of L2 and L3 (3mks)
l2 = x + 2y = -2
l3 = 2x - y = 1
2x + 4y = -4
2x - y = 1
5y = -5
y = -1
x + 2(-1) = -2
x - 2 = -2
x = 0
p (0, -1)
- The equation of L3 in the form y=mx +c (3mks)
- A straight line L1 whose equation is y-2x=4 meets the x-axis at M. Determine co-ordinates of M. (1mk)
- A curve is represented by the function y=x3 +x2 – x
- Find dy/dx (1mk)
y = x3 + x2 - x
dy/dx = 3x2 + 2x - 1 - Determine the values of y at the turning points of the curve y =x3 +x2 –x (4mks)

- Determine the nature of the turning points (2mks)

- In the space provided below, sketch the curve of y=x3+x2 –x (3mks)
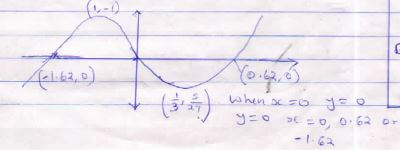
- Find dy/dx (1mk)
Download Mathematics Paper 1 Questions and Answers - Mathioya Mock 2021 Exams.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

