Instructions to candidates
- The paper contains TWO sections: Section I and Section II.
- Answer ALL the questions in section I and strictly any five questions from Section II.
- All answers and working must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non-programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise.
This paper consists of 17 printed pages.
For Examiner’s Use Only
Section I
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Total |
Section II
17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | Total |
|
|
|
|
|
|
|
|
|
QUESTIONS
- The length and width of a rectangle were measured as 12.4cm and 5.0cm respectively. Find to 4 significant figures, the percentage error in the area of the rectangle (3mks)
- Simplify
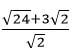(2mks) - A chord AB whose length is 8cm subtends an angle APB =60° at the circumference of a circle. Calculate to 4 significant figures;
- The perpendicular distance from the centre of the circle to the chord (2mks)
- The radius of the circle (2mks)
- Make h the subject of the formula (3mks)
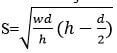
- Tap A takes 4 hours to fill a tank when empty, tap B takes 3 hours to fill the same tank when empty. Tap C takes 6 hours to empty the same tank when full. Tap A is opened then one hour later tap B and tap C are opened simultaneously. Calculate the total time it takes to fill the tank (3mks)
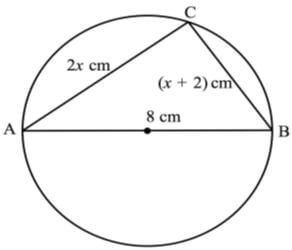
- In the figure below, AB is a diameter of the circle and AB=8cm, BC=(x+2)cm and AC=2x cm. Calculate the length of AC to 2 decimal places (4mks)
- Given that Cos 2x°=0.8070, find x to 1 decimal place when 0°≤x≤360° (4mks)
-
- Expand(3+x)6 upto the terms in x3 (2 marks)
- Use the expansion in (a) above to estimate (2.97)6 correct to 4 decimal places. (2 marks)
- The equation of a circle is x2 + y2 +4x − 2y − 20 = 0 . On the grid provided below, draw the circle.(4 mark)
- The weights of six boys in kilograms are 10,11, 12, 13, 14, and 15 while those of six girls are 8, 9, 10, 11,12 and 13. A boy and a girl are picked at random and the sum of their weight is recorded.
- Draw a probability space to show all the possible outcomes. (2 marks)
- Find the probability that the sum of their weights is at most 22 kilograms. (1 mark)
- Use completing the square method to solve: 3x2 + x −10 = 0 (3 marks)
- The value of a piece of land was Ksh. 400000 five years ago. Currently the piece of land is valued at Ksh. 587731.20 . Find the annual rate of appreciation of the piece of land. (3 marks)
- Find the length of an arc of a circle which subtends an angle of 0⋅8 radians at the centre of the circle. The radius of the circle is 15 cm. (3 marks)
- Lisa, a retailer buys two grades of rice. Grade A costing sh.90 per kilogram and grade B costing sh.120 per kilogram. She mixes the two grades of rice and sells the mixture at a cost of sh.127.5 per kilogram, making a profit of 25%. Find the ratio at which she mixed the two grades of rice. (3 marks)
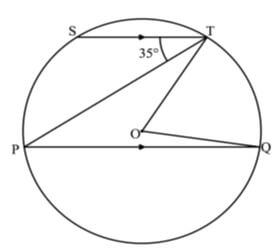
- The figure below O is the centre of the circle. PQ is parallel to ST and angle PTS = 35º. Find the size of reflex angle QOT (2 marks)
- Given that OP = −4 i ̃+10(j ̃), OQ = 2 i ̃+j ̃ and OR = 6 i ̃−5(j ̃). Show that the points P, Q and R are collinear. (3 marks)
Section II(50 marks)
Answer any five questions from this section in the spaces provided - The income tax rate of a certain year was as shown in the table below;
In that year Mwaniki’s monthly earnings were as follows; Basic salary Ksh 35400, House allowance Ksh 7000, Medical allowance Ksh 5000, Transport allowance Ksh 4520, Hardship allowance Ksh10400 .Monthly taxable income in Kenya shillings (Ksh) Tax rate percentage (%) in each shilling. 0 to 9680
9681 to 18800
18801 to 27920
27921 to 37040
37041 and above10
15
20
25
30
Mwaniki was entitled to a monthly tax relief of Ksh 1162.- Calculate Mwaniki’s;
- Taxable income (2 marks)
- Net tax (5 marks)
- Apart from income tax, the following monthly deductions were made; NHIF of Ksh 600, Sacco contributions of Ksh 1500 and 2% of his basic salary for widow and children pension scheme. Calculate Mwaniki’s monthly net income from his employment. (3mks)
- Calculate Mwaniki’s;
-
- A quantity y varies directly as the square of x and inversely as the square root of z. Given that y = 16 when x = 4 and z = 25,
- find the equation connecting y, x and z. (3 marks)
- if x is increased by 20% and z decreased by 36%, find the percentage change in y. (3 marks)
- The cost (C) per day of feeding examiners in a marking centre partly varies as the number of senior examiners (S) present and partly inversely as the number of ordinary examiners (P) present. It costs sh.32000 to feed 60 senior examiners and 400 ordinary examiners. The cost of feeding 80 senior examiners and 640 ordinary examiners is sh.41250. Find the cost of feeding 100 senior examiners and 500 ordinary examiners. (4 marks)
- A quantity y varies directly as the square of x and inversely as the square root of z. Given that y = 16 when x = 4 and z = 25,
- The 8th and the 15th terms of an Arithmetic sequence are 31 and 59 respectively.
- Find the first term and the common difference (3 marks)
- List the first 4 terms of the sequence (1 mark)
- Find the sum of the first 20 terms of the sequence (3 marks)
- Jeremy’s salary is Ksh980000 per annum. His salary increases by 10% annually. Calculate the total amount to the nearest Ksh he will have earned in 7 years. (3 marks)
- In the figure below O is the centre of the circle. MT is the tangent to the circle at point P. Angle PQS = 56°. PQRS are points on the circumference of the circle. SQT is a straight line.
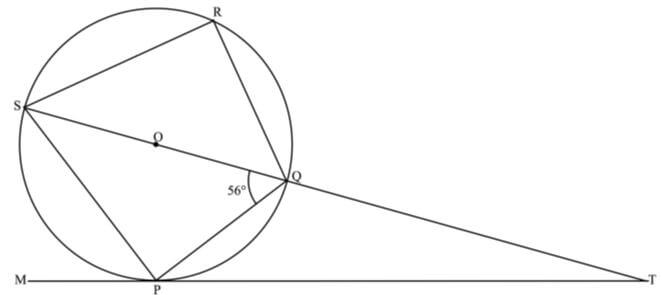
- Find:
- Angle PRQ (2 marks)
- Angle QPT (2 marks)
- Angle PTQ (2 marks)
- Given that QT = 5 cm and PT = 9.4 cm, calculate to 1 decimal place the area of the circle.
(Use π= 3.142) (4 marks)
- Find:
- Find the area enclosed by the curve y=x2 – 2x + 5 with the x-axis between x=2 and x=5 by using;
- Trapezium rule using 6 trapezia (4mks)
- Mid-ordinate rule using 3 mid-ordinate (4mks)
- Find the percentage error in using the mid-ordinate rule as compared to the trapezium rule (2mks)
- The marks scored by 40 students in mathematics test were as shown in the table below.
Mark
48-52
53-57
58-62
63-67
68-72
73-77
No of students
3
4
10
12
8
3
- Using an assumed mean of 64, calculate the mean mark (4mks)
- On the grid provided, draw the cumulative frequency curve for the data (3mks)
- Use the graph to estimate the semi interquartile range (3mks)
- A ship sails from A(0°,70°W) due North to B (25°N, 70°W) then due east to C(25°N,12°E) and finally a further 1800 nautical miles due East to D
- Calculate the total distance covered in nautical miles (4mks)
- If the whole journey took a total time of 300 hours, find its average speed in knots correct to 1 decimal place (2mks)
- Find to the nearest degree the final position of the ship (4mks)
- A quadrilateral ABCD has vertices A(4,−4),B(2,−4),C(2,−2) and D(4,−2)
- On the grid provided, draw the quadrilateral ABCD. (1 mark)
- AʹBʹCʹDʹ is the image of ABCD under a transformation represented by the matrix
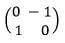
Find the coordinates of Aʹ, Bʹ, Cʹ and Dʹ,hence draw the quadrilateral AʹBʹCʹDʹ on the same grid provided. (3 marks) - Given that A’(4,4) is mapped onto A’’(−4,4) by a shear with the x −axis invariant, draw the quadrilateral A’’B’’C’’D’’ ,the image of A’B’C’D’ under the shear. (3 marks)
- Determine a single matrix that maps ABCD onto A’’B’’C’’D’’ (3 marks)
- On the grid provided, draw the quadrilateral ABCD. (1 mark)
(2mks)
MARKING SCHEME
- The length and width of a rectangle were measured as 12.4cm and 5.0cm respectively. Find to 4 significant figures, the percentage error in the area of the rectangle (3mks)
max area = 12.45 x 5.05 = 62.8725
min area = 12.35 x 4.95 = 61.1325
actual area = 12.4 x 5.0 = 62.0
absolute error = 62.8725 - 61.1325
2
% error = 0.87 x 100%
62
= 1.403% - Simplify 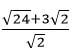(2mks)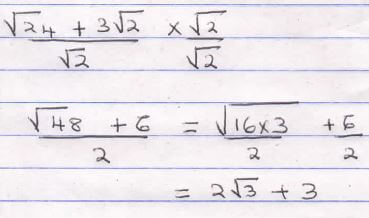
- A chord AB whose length is 8cm subtends an angle APB =60° at the circumference of a circle. Calculate to 4 significant figures;
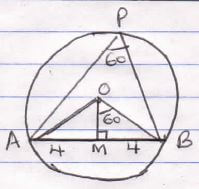
- The perpendicular distance from the centre of the circle to the chord (2mks)
Tan 60° = 4/h
h = 4 = 2.309
tan 60° - The radius of the circle (2mks)
Sin 60° = 4/r
r = 4/sin60°
= 4.619 cm
- The perpendicular distance from the centre of the circle to the chord (2mks)
- Make h the subject of the formula (3mks)
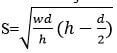
hs2 = 2wdh - wd2
2
2hs2 = 2wdh - wd2
wd2 = 2wdh - 2hs2
wd2 = h(2wd - 2s2)
h = wd2 or -wd2
2wd - 2s2 2s2 - 2wd - Tap A takes 4 hours to fill a tank when empty, tap B takes 3 hours to fill the same tank when empty. Tap C takes 6 hours to empty the same tank when full. Tap A is opened then one hour later tap B and tap C are opened simultaneously. Calculate the total time it takes to fill the tank (3mks)
Fraction of tank remaining after
1 hr = 1 - 1/4 = 3/4
3 taps after 1 hr full => 1/4 + 1/3 - 1/6 = 5/12
1 hr - 5/12
? - 3/4
Time to fill 3/4 = 3/4 x 1 x12/5 = 14/5
Total time => 1 + 14/5 = 24/5 hrs - In the figure below, AB is a diameter of the circle and AB=8cm, BC=(x+2)cm and AC=2x cm. Calculate the length of AC to 2 decimal places (4mks)
angle ACB = 90º (subtended by D)
(2x)2 + (x + 2)2 = 64
4x2 + x2 + 4x + 4 = 64
5x2 + 4x = 60
x2 + 0.8x = 12
x2 + 0.8x + (0.4)2 = 12 + 0.42
x = 3.087 or -3.887
AC = 2 x 3.087 = 6.17 cm - Given that Cos 2x°=0.8070, find x to 1 decimal place when 0°≤x≤360° (4mks)
cos-10.8070 = 36.196 = 36.2º
2x = 36.2 x = 18.1
2x = 323.8 x = 161.9
2x = 396.7 x = 198.1
2x = 683.8 x = 341.9 -
- Expand(3+x)6 upto the terms in x3 (2 marks)
1 6 15 20 36 35 34 33 x0 x1 x2 x3 729 + 1458x + 1215x2 + 540x3 - Use the expansion in (a) above to estimate (2.97)6 correct to 4 decimal places. (2 marks)
3 + x = 2.97
x = 2.97 - 3 = -0.03
729 + 1458(-0.03) + 1215(-0.03)2 + 540(-0.03)3
= 686.3389
- Expand(3+x)6 upto the terms in x3 (2 marks)
- The equation of a circle is x2 + y2 +4x − 2y − 20 = 0 . On the grid provided below, draw the circle.(4 mark)
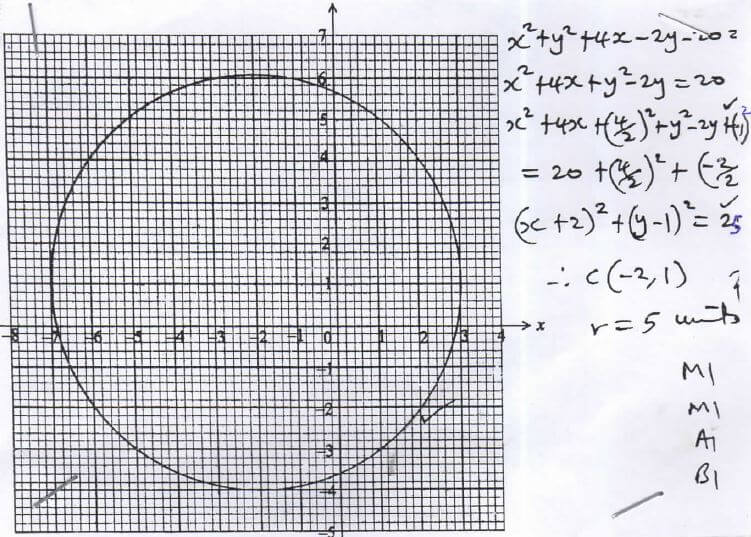
- The weights of six boys in kilograms are 10,11, 12, 13, 14, and 15 while those of six girls are 8, 9, 10, 11,12 and 13. A boy and a girl are picked at random and the sum of their weight is recorded.
- Draw a probability space to show all the possible outcomes. (2 marks)
10 11 12 13 14 15 8 18 19 20 21 22 23 9 19 20 21 22 23 24 10 20 21 22 24 24 25 11 21 22 23 25 25 26 12 22 23 24 26 26 27 13 23 24 25 27 27 28 - Find the probability that the sum of their weights is at most 22 kilograms. (1 mark)
15/36
- Draw a probability space to show all the possible outcomes. (2 marks)
- Use completing the square method to solve: 3x2 + x −10 = 0 (3 marks)
x2 + x/3 = 10/3
x2 + x/3 + (1/6)2 = 10/13 + (1/6)2
(x + 1/6)2 = 3.3611
x + 1/6 = ± 1.8333
x = 1.8333 - 0.1667
= 1.6667 = 12/3
x = -1.8333 - 0.1667
= -2 - The value of a piece of land was Ksh. 400000 five years ago. Currently the piece of land is valued at Ksh. 587731.20 . Find the annual rate of appreciation of the piece of land. (3 marks)
A = P (1 + r/100)s
587731.20 = 400,000 (1 + r/100)5
1.469328 = (1 + r/100)5
1 + r/100 = 1.08
r/100 = 0.08
r = 8% - Find the length of an arc of a circle which subtends an angle of 0⋅8 radians at the centre of the circle. The radius of the circle is 15 cm. (3 marks)
c/15 = 0.8
c = 15 x 0.8
= 12cm - Lisa, a retailer buys two grades of rice. Grade A costing sh.90 per kilogram and grade B costing sh.120 per kilogram. She mixes the two grades of rice and sells the mixture at a cost of sh.127.5 per kilogram, making a profit of 25%. Find the ratio at which she mixed the two grades of rice. (3 marks)
125% = 127.5
100% = 100 x 127.5 = 102
125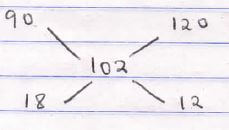
18 : 12
3 : 2 - The figure below O is the centre of the circle. PQ is parallel to ST and angle PTS = 35º. Find the size of reflex angle QOT (2 marks)
TPQ = 35º
QOT = 70º
Reflex = 360 - 70
= 290 º - Given that OP = −4 i ̃+10(j ̃), OQ = 2 i ̃+j ̃ and OR = 6 i ̃−5(j ̃). Show that the points P, Q and R are collinear. (3 marks)
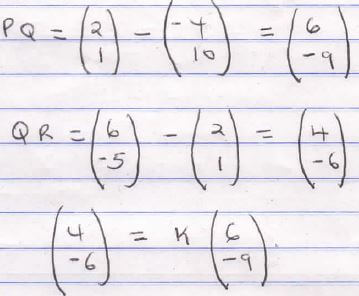
4 = 6k
k = 2/3
QR = 2/3 PQ hence parallel
Q is common hence collinear
Section II(50 marks)
Answer any five questions from this section in the spaces provided - The income tax rate of a certain year was as shown in the table below;
In that year Mwaniki’s monthly earnings were as follows; Basic salary Ksh 35400, House allowance Ksh 7000, Medical allowance Ksh 5000, Transport allowance Ksh 4520, Hardship allowance Ksh10400 .Monthly taxable income in Kenya shillings (Ksh) Tax rate percentage (%) in each shilling. 0 to 9680
9681 to 18800
18801 to 27920
27921 to 37040
37041 and above10
15
20
25
30
Mwaniki was entitled to a monthly tax relief of Ksh 1162.- Calculate Mwaniki’s;
- Taxable income (2 marks)
=35400 + 7000 + 5000 + 4520 + 10400
=sh 62 320 - Net tax (5 marks)
1st tax = 9680 x 0.1 = sh 968
2nd tax = 9120 x 0.15 = sh 1368
3rd tax = 9120 x 0.2 = sh 1824
4th tax = 9120 x 0.25 = sh 2280
5th tax = 25280 x 0.3 = sh 7584
gross tax = sh 14024
net tax = 14024 - 1162
= sh 12862
- Taxable income (2 marks)
- Apart from income tax, the following monthly deductions were made; NHIF of Ksh 600, Sacco contributions of Ksh 1500 and 2% of his basic salary for widow and children pension scheme. Calculate Mwaniki’s monthly net income from his employment. (3mks)
deductions = 12862 + 600 + 1500 + 2/100 x 35400
= 15670
62320 - 15670 = sh 46650
- Calculate Mwaniki’s;
-
- A quantity y varies directly as the square of x and inversely as the square root of z. Given that y = 16 when x = 4 and z = 25,
- find the equation connecting y, x and z. (3 marks)
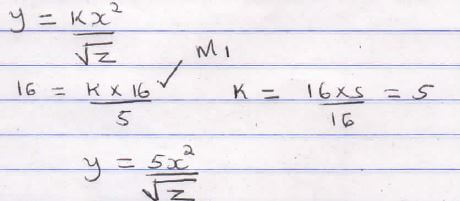
- if x is increased by 20% and z decreased by 36%, find the percentage change in y. (3 marks)
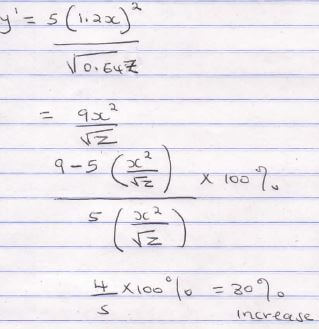
- find the equation connecting y, x and z. (3 marks)
- The cost (C) per day of feeding examiners in a marking centre partly varies as the number of senior examiners (S) present and partly inversely as the number of ordinary examiners (P) present. It costs sh.32000 to feed 60 senior examiners and 400 ordinary examiners. The cost of feeding 80 senior examiners and 640 ordinary examiners is sh.41250. Find the cost of feeding 100 senior examiners and 500 ordinary examiners. (4 marks)
c = ms + n/p
3200 = 60m + n/400
12800000 = 24000m + n .....(i)
41250 = 80m + n/640
36400000 = 51200m + n .....(ii)
13600000 = 27200m
27200 27200
m = 500
n = 800,000
c = 500s + 800,000
p
c = 500(100) + 800,000
500
c = sh 51, 600
- A quantity y varies directly as the square of x and inversely as the square root of z. Given that y = 16 when x = 4 and z = 25,
- The 8th and the 15th terms of an Arithmetic sequence are 31 and 59 respectively.
- Find the first term and the common difference (3 marks)
a + 7d = 31
a + 14d = 59
7d = 28
d = 4
a + 28 = 31
a = 3 - List the first 4 terms of the sequence (1 mark)
3, 7, 11, 15 - Find the sum of the first 20 terms of the sequence (3 marks)
20th term = 3 + (19 x 4) = 79
s20 = 20/2 (3 + 79)
= 820 - Jeremy’s salary is Ksh980000 per annum. His salary increases by 10% annually. Calculate the total amount to the nearest Ksh he will have earned in 7 years. (3 marks)
110 x 980,000 = 1078000
100
r = 1078000 = 1.1
98000
sn = a(rn - 1)
r - 1
= 98000 (1.17 - 1)
0.1
= sh 9297428
- Find the first term and the common difference (3 marks)
- In the figure below O is the centre of the circle. MT is the tangent to the circle at point P. Angle PQS = 56°. PQRS are points on the circumference of the circle. SQT is a straight line.
- Find:
- Angle PRQ (2 marks)
QPS = 90º
QPS = PRQ = 34º - Angle QPT (2 marks)
QPT = 34º (alternate angle theorem) - Angle PTQ (2 marks)
PQT = 124º
PTQ = 180º - (124 + 34)
= 22º
- Angle PRQ (2 marks)
- Given that QT = 5 cm and PT = 9.4 cm, calculate to 1 decimal place the area of the circle.
(Use π= 3.142) (4 marks)
let the diametre SQ = x
5(x + 5) = 9.42
5x + 25 = 88.36
5x = 63.36
x = 12.672
area = 3.142 x ( 12.672/2)2
= 1261 cm2
- Find:
- Find the area enclosed by the curve y=x2 – 2x + 5 with the x-axis between x=2 and x=5 by using;
x 2.0 2.5 3.0 3.5 4.0 4.5 5.0 y 5 6.25 8 10.25 13.0 16.25 20 - Trapezium rule using 6 trapezia (4mks)
A = 1/2 x 0.5 [{5 + 20) + 2(6.25 + 8 + 10.25 + 13 + 16.25)]
= 0.25 (25 + 2(53.75))
= 0.25 (25 + 107.5)
= 33.125 sq units - Mid-ordinate rule using 3 mid-ordinate (4mks)
y1 = 6.25 y2 = 10.25 y3 = 16.25
A = 1(6.25 + 10.25 + 16.25)
= 32.75 - Find the percentage error in using the mid-ordinate rule as compared to the trapezium rule (2mks)
% error = (33.125 - 32.75) x 100%
33.125
= 0.375 x 100%
33.125
= 1.132%
- Trapezium rule using 6 trapezia (4mks)
- The marks scored by 40 students in mathematics test were as shown in the table below.
Mark
48-52
53-57
58-62
63-67
68-72
73-77
No of students
3
4
10
12
8
3
- Using an assumed mean of 64, calculate the mean mark (4mks)
x = 64 + -25x f t ft 50 3 -14 -42 55 4 -9 -36 60 10 -4 -40 65 12 1 12 70 8 6 48 75 3 11 33 40 -25
40
= 63.375 - On the grid provided, draw the cumulative frequency curve for the data (3mks)
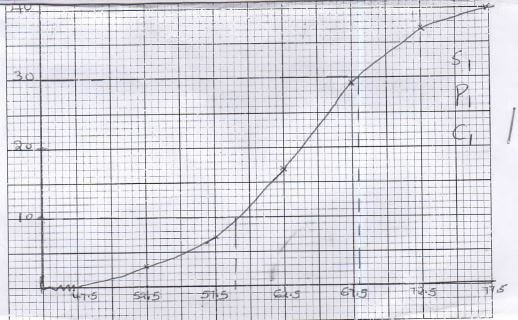
- Use the graph to estimate the semi interquartile range (3mks)
Q1 = 59 mk
Q3 = 68 mk
semi interquatile range = 68 - 59
2
= 4.5
- Using an assumed mean of 64, calculate the mean mark (4mks)
- A ship sails from A(0°,70°W) due North to B (25°N, 70°W) then due east to C(25°N,12°E) and finally a further 1800 nautical miles due East to D
- Calculate the total distance covered in nautical miles (4mks)
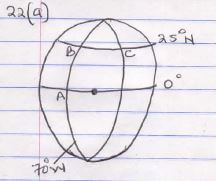
AB = 60 x 25
= 1500 nm
BC = 82 x 60cos25
= 4459.034 nm
Total distance = 1500 + 4459.034 + 1800
= 7759.034 nm - If the whole journey took a total time of 300 hours, find its average speed in knots correct to 1 decimal place (2mks)
Average speed = 7759.034
300
= 25.863
= 25.9 knots - Find to the nearest degree the final position of the ship (4mks)
1800 = α x 60 cos 25
α = 1800 = 33º
60 cos 25
longitude = 33 + 12 = 45ºE
Position = (25ºN, 45ºE)
- Calculate the total distance covered in nautical miles (4mks)
- A quadrilateral ABCD has vertices A(4,−4),B(2,−4),C(2,−2) and D(4,−2)
- On the grid provided, draw the quadrilateral ABCD. (1 mark)
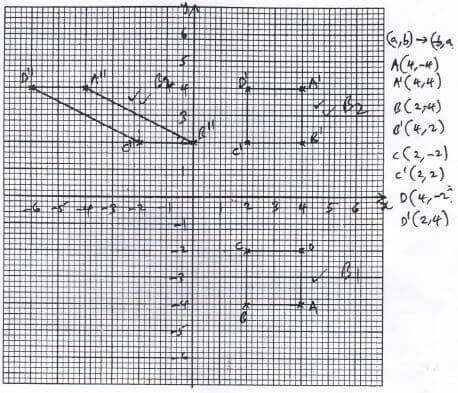
- AʹBʹCʹDʹ is the image of ABCD under a transformation represented by the matrix
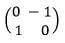
Find the coordinates of Aʹ, Bʹ, Cʹ and Dʹ,hence draw the quadrilateral AʹBʹCʹDʹ on the same grid provided. (3 marks)
A1(4, 4)
B1(4, 2)
C1(2, 2)
D1(2, 4) - Given that A’(4,4) is mapped onto A’’(−4,4) by a shear with the x −axis invariant, draw the quadrilateral A’’B’’C’’D’’ ,the image of A’B’C’D’ under the shear. (3 marks)
d = -2A - Determine a single matrix that maps ABCD onto A’’B’’C’’D’’ (3 marks)
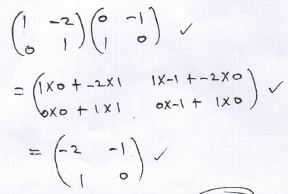
- On the grid provided, draw the quadrilateral ABCD. (1 mark)
Download Mathematics Paper 2 Questions and Answers - Mathioya Mock 2021 Exams.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students
Join our whatsapp group for latest updates
