QUESTIONS

SECTION I (50MARKS)
Answer ALL Questions in this Section

1. Evaluate the following; (3 marks)
   
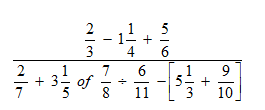
2. Use square roots, reciprocal and square tables to evaluate to 4 significant figures the expression;  (3 marks)
   (0.06458)^½+ (    2 ²   )
                         0.4327
3. Solve for x in the equation ½log₂81 + log₂(x² - ^x/₃) = 1(3marks)
4. A farmer has a piece of land measuring 840m by 396m.  He divides it into square plots of equal size.  Find the maximum area of one plot. (3 marks)
5. The following data was obtained from the mass of a certain animal. Complete the tableand the histogram below. (3 marks)
   

   Mass(kg)	Frequency
   41-50	20
   51-55
   56-65	40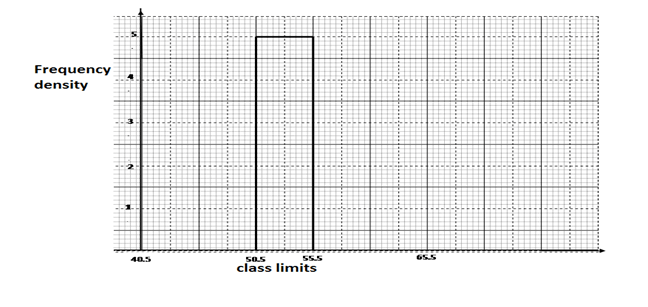

   
   
6. Solve the following inequalities and state the integral values (3 marks)
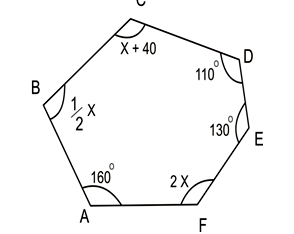
   2x – 2 ≤ 3x + 1 < x + 11 
7. The figure below shows a regular polygon A B C D E F with the interior angles indicated.  Find the value of the smallest angle in the polygon. (3 marks)
   
8. The figure below represents a plot of land ABCD such that AB=85m, BC=75m, CD=60m, DA=50m and angle ACB = 90º. (Not drawn to scale).
   
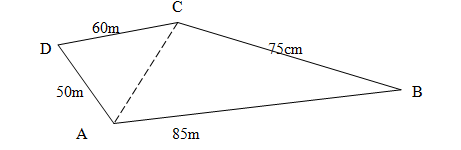
   Determine the area of the plot, in hectares, correct to two decimal places. (3marks)
9. A rectangular tank has a hole in it such that 11cm³ of water leaks out every 5 seconds. Using π as 3.142. Calculate:-
   1. The capacity of the water lost from the tank every hour. (2marks)
   2. The time it takes to fill a cylindrical tank of radius 30cm and height 30cm into which the leaking water drains; in hours to 4 significant figures. (2marks)
10. Find the value of x if. (3 marks)
    (²⁷/₈)^x+7 = (⁴/₉)^-3x
11. The image of a point K(1,2) after translation is K1 (-1,2). What is the coordinate of the point R whose image is R1 (-3,3) after undergoing the same translation. (3 marks)
12. Mugo, a fruit vendor obtained a total of Kshs. 6144 from her sales of oranges on Monday at Kshs. 8.00 each. She had bought 560 more oranges to add to what had remained on Sunday where she had sold 240 more oranges than on Saturday. She had sold 750 oranges on Saturday. Calculate the total number of oranges Mugo had bought on Saturday. (4 marks)
13. Simplify the following expression by reducing it to a single fraction. (3 marks)
    2x-3 -  x-2 - 1-x
      3        2       4
14. Water and ethanol are mixed such that the ratio of the volume of water to that of ethanol is 3: 1. Taking the density of water as 1 g/cm³ and that of ethanol as 1.2g/cm³, find the mass in grams of 2.5 litres of the mixture.  (3 marks)
15. A Kenyan bureau buys and sells foreign currencies as shown below
                                       Buying(In Kenya Shillings)     Selling(In Kenya shillings) 
    1 Hong Kong dollar                   9.74                                        9.77
    100 Japanese Yen                   75.08                                      75.12
    A tourists arrived in Kenya with 105 000 Hong Kong dollars and changed the whole amount to Kenyan shillings.While in Kenya, she pent Kshs 403 897 and changed the balance to Japanese Yen before leaving for Tokyo. Calculate the amount, in Japanese Yen that she received. (3 marks)
16. Draw triangle ABC such that AB=4.4cm, BC=4cm and angle ABC=1200, construct an orthocenter of the triangle ABC and mark it X. (3 marks)

SECTION II (50 MARKS)
Answer FIVE questions ONLY from this section

17. A line L₁ passes through the points (-2,3) and (-1,6) and is perpendicular to L₂ at (-1,6).
    1. Find the equation of L₁. (2 marks)
    2. Find the equation of L₂ in the form ax+by-c=0 where a, b and c are constants. (2 marks)
    3. Given that another line L₃ is parallel to L₁ and passes through point (1,2) , find the x and y intercepts of L₃. (3 marks) 
    4. Find the point of intersection of L₂ and L₃.   (3 marks)
18. A sector of angle 1080 is cut from a circle of radius 20 cm. It is folded to form a cone. Calculate to 1 decimal place: (use π=²²/₇)
    1. The curved surface area of the cone. (2 marks)
    2. The base radius of the cone. (3 marks)
    3. The vertical height of the cone. (2 marks)
    4. If 12 cm of the cone is chopped off to form a frustum as shown below.
       
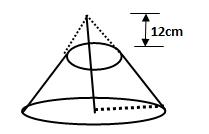
       Calculate the volume of the frustum formed. (3 marks)
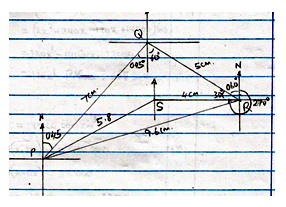
19. A village Q is 7 km from village P on a bearing of 045º. Village R is 5 km from village Q on abearing of 120º and village S is 4 km from village R on a bearing of 270º.
    1.  Taking a scale of 1 m to represent 1 Km, locate the three villages.(3 marks)
    2. Use the scale drawing to find the:
       1. Distance and bearing of the village R from village P. (2 marks) 
       2. Distance and bearing of village P from village S. (2 marks)
    3. Calculate the area enclosed by the three villages (3 marks)
20. The floor of a rectangular room can be covered completely by a carpet costing sh. 200 per square metre. The total cost of the carpet would be sh. 5600.  Taking the length of the room to be x m;
    1. Express width of the room in terms of x (2marks) 
    2. If a uniform width of ½ m is left uncovered all round.  The cost is sh. 2000 less. Form and solve an equation to determine the value of x. (5marks)
    3. Later it was decided that the floor left uncovered in (b) above should also be covered. However the cost of the carpet had then gone up by sh. 150 per square metre.  Determine the cost in covering the previously uncovered region. (3marks)
21.      
    1. Given that the matrix A = (²₃ ³₄) , find A-1, the inverse of A. (2 marks)
    2. Kariuki bought 400 goats and 600 sheep for a total of Kshs 1,700,000. Maina bought 180 goats and 240 sheep for a total of Kshs 720,000. If the price of a goat is sh. X and that of a sheep is shs y,
       1. Form two equations to represent the above information. (2 marks)
       2. Use the matrix A^-1 to find the price of one goat and one sheep. (3 marks)
    3. John bought 450 goats and 720 sheep. He was given a total discount of shs 66,600.
       If the discount on the price of a goat was 2%, calculate the percentage discount on the price of a goat. (3 marks)
22. The distance between two towns A and B is 460 km. a minibus left town A at 8.45 am and travelled towards B at an average speed of 65km/hr. A matatu left B at 10.55 am on the same day and travelled towards A at an average speed of 80km/hr.
    1. How far from town B did they meet? (4 marks)
    2. At what time did the two vehicles meet? (2 marks)
    3. A motorist started from his home at 9.15am on the same day and travelled to B at an average speed of 120km/hr. he arrived at the same time as the minibus. Calculate the distance from B to his home. (4 marks)
23. Three partners Mutua, Muthoka and Mwikali contributed Sh. 600,000, Sh. 400,000 and Sh. 800,000 respectively to start a business of a matatu plying Mbumbuni – Machakos route. The matatu carries 14 passengers with each paying Sh. 250. The matatu makes two round trips each day and ever full. Each day Sh. 6000 is used to cover running costs and wages.
    1. Calculate their net profit per day. (2 marks)
    2. The matatu works for 25 days per month and is serviced every month at a cost of KSh.10,000. Calculate their monthly profit in June. (1 mark)
    3. The three partners agreed to save 40% of the profit, 24% is shared equally and the rest to be shared in the ratioof their contribution. Calculate Muthoka’s share in the month of June. (4 marks)
    4. The matatu developed mechanical problems and they decided to sell it through an agent who charged a commission of 5% on selling price. Each partner received KSh. 475,000 from the agent after he had taken his commission. Determine the price at which the agent sold the matatu. (3 marks)
24. The displacement S metres of a body moving along a straight line after t seconds is given by  S = -2t³ + ³/₂t² + 3t
    1. Find its initial acceleration. (3 marks)
    2. Calculate:-
       1. The time when the body was momentarily at rest. (3 marks)
       2. Its displacement by the time it comes to rest momentarily (2 marks)
    3. Calculate the maximum velocity attained (2 marks)

MARKING SCHEME

1. ²/₃ + ⁵/₆ = 4+5 = ⁹/₆ -  ⁵/₄= 18-15=  ³/₁₂ = ¼
                     6                        12
   ¹⁶/₃ + ⁹/₁₀ = 160+27= ¹⁸⁷/₃₀    ¹⁶/₅ × ⁷/₈ × ¹¹/₆ =  ⁷⁷/₁₅
                         30
   ²/₇ + ⁷⁷/₁₅ = 30+539 =  ⁵⁶⁹/₁₀₅ - ¹⁸⁷/₃₀=  = ^-57/₇₀      
                       105
   ¼ × ^-70/₅₇ = ^-35/₁₄₄ 
2. √(6.458 ×10^-2 )+ 2(    1     )²
                                 0.4327
   2.541 x 10^-1 + (2 x 2.311)²
   = 0.2541 + (4.622)²
   = 0.2541 + 21.363
   = 21.62
3. log₂9 + log₂(x²- ^x/₃) = log2²
   9x²- 3x-2=0
   (3x+1)(3x-2)=0
   x= ^-1/₃ or ²/₃  
4. 840 = 2³×3×5×7 
   396= 2²×3²×11
   G.C.D = 2²×3²=12
   Area = 12 × 12=144
5.     
   

   Mass(kg)	Frequency
   41-50	20
   51-55	25
   56-65	40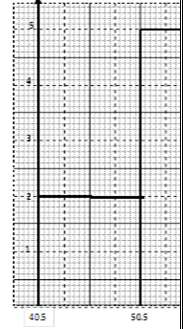

   
   
6. 2x - 2 ≤ 3x+1
   -2 – 1 ≤ 3x-2x
   -3 ≤x B1 for -3≤x
   3x + 1 < x + 11
   2x < 10
   X < 5 B1 for x < 5
   -3 ≤x<5
   Integral values   -3,-2, -1, 0, 1,2,3,4 B1 – All correct integral values
7. Sum of int. angles = (2n-4)90=(2(6)-4)90=720
   ½+4x+40+2x+160+110+130=720
   x=80
   smallest angle=40º
8. AC = √(85² -75²) =  40M
   Area of quadrilateral  A B C D
   = ½×40×75+75+75(75-60)(75-50)(75-40)
   = 2492m²
   In hectares;  2492   = 0.2492 ≈ 0.25ha
                      10,000
9.           
   1. In 1 hour:
      11 x 3600  = 7920cm³
             5
      Capacity of water lost = 7.92 litres
   2. Volume of tank = 3.142 x 302 x 30
                                    = 84834cm³
                                    = 84.834 litres
      Time = 84.834
                    7.92
      =  10.711 ~ 10.71 hours
10. (3³)^x+7 = (3 ²)^3x
     2³           2²
    (³/₂)^3x+21=(³/₂)^6x
    3x  + 21  = 6x
    3x  =  21
    x = 7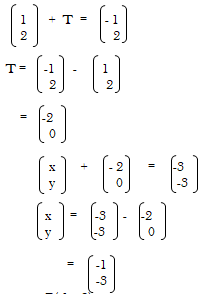
11. 
    
    R(-1, -3)
12. No. of oranges sold on Monday;
    6144   = 768
      8
    No. of oranges that remained on Sunday;
    768 – 560  = 208
    No. of oranges bought on Saturday.
    208 + 750  + 750 + 240
    = 1948
13. 2x-3 -  x-2 - 1-x 
      3        2       4
    4(2x-3)- 6(x-2)-3(1-x)
                 12
    = 8x -12-6x+12-3+3x
                    12
    = 5x -3
         12 
14. Vol of water: ¾ x 2.5 = 1.875l
    Vol of ethanol ¼ x2.5 = 0.625l
    Mass of water 1875 x 1 = 1875g
    Mass of ethanol 625 x 1.2 = 759g
    Mass of mix= 1875 + 750=2625g
15. 15 9.74 x 105,000=Ksh.1,022,700
    1,022,700-403897=Ksh.618,803
    618803 x 100 = 832,752.66 yen
         75.12
16.      
    
17.         
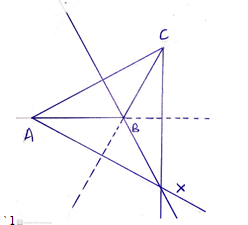
    1. m₁ =  6-3  =3
              -1+2
       ³/₁ = y-3 
              x+2
       y-3=3(x+2)
       y=3x+9
    2. m₂ = -¹/₃
       ^-1/₃ = y-6 
                x+1 
       3y-18=-x-1 
       x+3y-17=0 
    3. m₃ = 3
       ³/₁ = y-2 
              x - 2
       y = 3x -1
       At x intercept; y=0,x=¹/₃;x-intercept = ¹/₃
       At y intercept; x=0,y=-1;y intercept=-1
    4. At point of intersection, y values are equal
       3x-1=^-x/₃ + ¹⁷/₃
       9x-3=-x+17 
       10x=20; x=2
       y=3(2)-1=5
       Point of intersection (2, 5) M 1
18.         
    1. 108  x 22  x 20 x 20
        36      7 
       377.14
    2. 3.77.14 = ²²/₇ x  r  x 20
       r= 377.14 x 7
             22 x 20
       r = 6.0
    3. h² + 6² = 20²
       h = √(20² – 6²)
       h = 19.079
       h = 19.1
    4. 19.08 = 6 
         12       r
       r = 3.774
       Volume of smaller cone = ¹/₃ × ²²/₇ (3.774)² x 12
       = 179.1
       Volume of  larger cone ¹/₃ × ²²/₇ (6)² x 19.08
       = 719.6
       719.6 - 179.1
       = 540.5
19.      
    1.           
       
    2.      
       1. 9.6 km + 0.1
          75º ± 0.1
       2. 5.8 km + 0.1
          2460 + 0.1
       3. Area = ½ x 7 x 5 sin 105º – ½ x 4 x 5.8 sin 154
          = 16.90370196 – 5.085105303
          = 11.81859666
          = 11.82 cm²                 
20. w = ²⁸/_x
    Area = (x-1)(²⁸/_x) = ³⁶⁰⁰/₂₀₀
    (x-1) (²⁸/_x-1) = 18 
    28 – x - ²⁸/_x + 1 – 18 = 0 
    -x - ²⁸/_x + 11 = 0 
    x² + 28 - 11x = 0
    x² - 11x + 28 = 0
    x² - 7x - 4x + 28 = 0
    x(x-7) - 4(x-7) = 0 
    (x-7) (x-4) = 0
    x = 7 or x = 4
    Length = 7m
    Area not previously covered = 28 – 18 m²
    = 10 m²
    Cost = 10 × (200+150)
    = 10 × 350
    = sh. 3500 
21.        
    1. det = 8 - 9 = -1
    2.          
       1. 400x + 600y = 1700000
          2x + 3y = 8500
          180x + 240y = 720000
          3x + 4y = 12000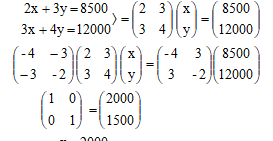
       2. 
          
          x = 2000
          y = 1500
          Cost of a goat = sh2000/-
          cost of a sheep = sh1500
    3. Discount sheep = ²/₁₀₀ x 1500 x 720
       = shs 21600
       discount on goats = shs(66,600 - 21,600)
       = shs 45000
       45000 = ^x/₁₀₀ x 450 x 2000
       x =  45000  = 5
            450 x 20
       percentage discount on a goat = 5%
22.        
    1. Distance of A before B started= 65 × 2 ¹/₆
       =140.83km
       Distance shared = 460-140.83
       =319.17km
       Time to meet = 319.17km
                                    145
       =2.2011hrs
       Distance from B =80 × 2.2011
       =176.09km
    2. Time ≈2hrs 12 minutes
       Meeting time=1055hrs+2hrs 12 min
        =1307hrs
       =1.07pm
    3. Time taken by minibus= ⁴⁶⁰/₆₅
       ≈7 hrs 05minutes
       Time to reach B= 0845hrs+7 hrs 5 mins
       =1550hrs
       = 3.50pm
       Time of the motorist= 1550hrs-0915hrs
       =6hrs 35minutes
       Distance= 120×6³⁵/₆₀
                          =790km
23.        
    1. 250 x 14 x 2 x 2 = 14000
       Net profit = 14000 – 6000
       = KSh. 8000
    2. 8000 x 25 = 200,000
       = 190,000
    3. Saving: ⁴⁰/₁₀₀ x 190,000
       = 76000
       Remaining profit = ³⁶/₁₀₀ x 190,000
       = 68,400
       Muthoka’s share
       45,600 + ²/₉ x 68,400
           3
       = 30,400
    4. 475,000 x 3 x 100
                   95
       = 1,500,000 
24.            
    1. Initial acceleration is at t = 0
       V=^ds/_dt = - 6t² + 3t + 3
       a = ^dv/_dt = -12t + 3
       when t = 0, a =[0 + 3]
       a = 3m/s²
    2.              
       1. at rest V = 0
          -6t²+ 3t + 3 = 0
          (2t + 1) (t-1) = 0
          t = -½ or t = 1 (t = -1/2 not applicable)
       2. S = -2t³ + ³/₂t² + 3t
          When t =m 1, s = -2(1)³ + ³/₂ (1)² + 3 (1)
          2.5M
    3. When velocity is maximum, a = 0
       -12t + 3 = 0
       t = ¼
       Max v = -6 (¼)² + 3(¼) + 3 = 3.375 m/s