Mathematics Paper 1 Questions - Maseno Mock Examinations 2022

QUESTIONS

SECTION I (50 Marks)
Answer all the questions in this section in the spaces provided.

1. Evaluate   -2 x -3-(-4)   of 0.8 without using a calculator. (3 marks)
                  10 ÷(-5) x -2²
2. A man withdrew some money from a bank. He spent ³/₁₀ of the money on his daughter’s school fees and ³/₅ of the remainder on his son’s school fees. If he remained with Ksh 10 500, calculate the amount of money he spent on son’s school fees. (3 marks)
3. Simplify the expression 3x² + 2xy - y²
                                           18x² - 2y²
4. Given that sin(x + 25)º = cos(2x + 35)º, find the exact value of tan(3x)º (3 marks)
5. Solve the equation 27^x + 3^3x-1 - 4 = 104 . (3 marks)
6. A Kenyan bank buys and sells foreign currencies as shown below.
                                   Buying (Ksh)   Selling (Ksh)
                1 Euro              118.69        118.75
   100 Japanese Yen          87.10          87.45
   A businessman travelling from France arrived in Kenya with 19 500 Euros. He converted all the money into Kenya shillings at the bank. While in Kenya, he bought a car for Ksh 1 200 000 and spent another Ksh 87 000 then he converted the remaining amount into Japanese Yen. Calculate the amount to the nearest Yen that he received. (3 marks)
7. Solve the inequality 5 - 2x < ½ x ≤ x + 2 and represent the solution on a number line. (3 marks)
                                                             3
8. Use tables of reciprocals and square roots to evaluate   3      + √0.4036 (3 marks)
                                                                                         0.521
9. The interior angle of a regular polygon is (3x + 30)º while the exterior angle is 2x . Find the sum of the interior angles of the polygon. (3 marks)
10. In the figure below, ABCD is a parallelogram in which AB = 12 cm, BC = 8 cm and angle ABC 108º
    
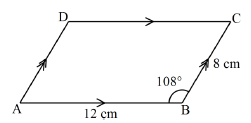
    Calculate the area of the parallelogram correct to 3 significant figures. (3 marks)
11. A steel company wishes to make nails from steel rods of length 5.12 m, 7.60 m and 9.28 m. Find the least number of nails that can be obtained from the three steel rods. (4 marks)
12. Given that OA = 2i - 3j and OB = 4j - i , find the magnitude of AB correct to 2 decimal places. (3 marks)
13. Given that 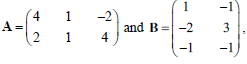 find the inverse of AB. (3 marks)
14. The figure below represents a speed time graph for a leopard which covered 800 metres in 45 seconds.
    
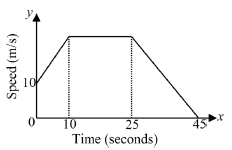
    Calculate:
    1. The maximum speed in km/h attained by the leopard. (3 marks)
    2. The deceleration of the leopard during the last 15 seconds. (1 mark)
15. A two digit number is such that the sum of its digits is 12. When the digits are interchanged, the original number is increased by 18. Find the original number. (3 marks)
16. Using a ruler and a pair of compasses only, construct a trapezium ABCD in which AB = 5 cm ,AD = 6 cm, DC = 10 cm, ∠BAD = 105º and AB is parallel to DC. Draw a perpendicular from B to DC hence measure the height of the trapezium. (3 marks)

SECTION II (50 Marks)
Answer only five questions from this section in the spaces provided.

17. A construction company makes concrete by mixing cement, sand and ballast such that the ratio of cement to sand is 1:2 and that of sand to ballast is 3:4.
    1. Determine:
       1. The ratio of cement to ballast in the concrete. (2 marks)
       2. The number of bags of ballast required to make a concrete with 27 bags of sand. (2 marks)
    2. The cost of a bag of cement, sand and ballast is Ksh 680, Ksh 136 and Ksh 102 respectively. Calculate the cost of one bag of concrete. (2 marks)
    3. The construction company requires to transport 30 tonnes of sand to a site using a tractor. The tractor carries a maximum of 3 600 kg of sand and costs Ksh 8 000 per trip.
       Calculate the least amount of money required to transport the sand to the site. (4 marks)
18. A straight line L₁ passes through the points P(3,2) and Q(1,8).
    1. Find the equation of the line L₁ in the form ax + by + c = 0 where a, b and c are integers. (3 marks)
    2. The line L₁ meets the x – axis at R.
       1. Find the coordinates of R. (1 mark)
       2. Another line L₂ is perpendicular to L₁ at R. Find the equation of L₂ in the form y = mx + c where m and c are constants. (3 marks)
    3. A third line L₃ is parallel to L₂ and passes through the point (-12,5) . Find the point where L₃ and L₁ intersect. (3 marks)
19. A solid frustum of a cone with base radius 10.5 cm and top radius 7 cm is made of a material whose density is 10 g/cm³. The mass of the solid is 58.52 kg.
    1. Determine the volume of:
       1. The frustum in cm³. (2 marks)
       2. The cone that was cut off to obtain the frustum in cm³. (3 marks)
    2. Find the height of:
       1. The cone that was cut off to obtain the frustum. Take π = ²²/₇ (3 marks)
       2. The frustum. (2 marks)
20. The vertices of a triangle ABC are A(1,1), B(4,1) and C(6,4) .
    1. On the grid below, draw the triangles.
       1. ABC. (1 mark)
       2. A'B'C' , the image of triangle ABC under a negative quarter turn about the origin. (2 marks)
       3. A''B''C'', the image of triangle A'B'C' under reflection in the line y=x . (2 marks)
    2. Triangle A'''B'''C''' with vertices A'''(-1,-5), B'''(-4,-5) and C'''(-6,-2) is the image of triangle A''B''C'' under a transformation T.
       1. Draw the triangle A'''B'''C'''. (1 mark)
       2. Describe fully the transformation T. (2 marks)
    3. State any pair of triangles which are:
       1. Directly congruent. (1 mark)
       2. Oppositely congruent. (1 mark)
21. The exact area bounded by the curve y = 3x² + kx + 2 , the x – axis and the lines x=0 and x=6 is 300 square units.
    1. Determine the value of k. (3 marks)
    2. Estimate the area bounded by the curve y = 3x² + kx + 2, the x – axis and the lines x = 0 and x = 6 using:
       1. Trapezium rule with 6 strips. (3 marks)
       2. Mid – ordinate rule with 6 strips. (4 marks)
22. The data below represents marks scored by 50 students in a test.
    46 73 48 73 62 58 67 61 67 67
    51 75 60 52 63 56 74 64 53 68
    59 81 61 57 66 66 76 55 84 70
    61 51 65 59 49 54 83 63 79 69
    65 58 66 62 53 66 50 64 68 71
    1. Using a class width of 5 and starting with the score of 46, make a frequency distribution table for the data. (2 marks)
    2. Using the table in (a) above, estimate:
       1. The mean score. (3 marks)
       2. The median score. (3 marks)
    3. Represent the information in the table in (a) above in a histogram. (2 marks)
23. In the figure below, ABCD is a trapezium in which AB = 17 cm, AD = 16 cm and angle ABC 150º . AB is parallel to DC and AB = BD.
    
    
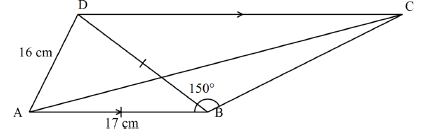
    1. Calculate the area of triangle ABD. (2 marks)
    2. Calculate correct to 2 decimal places:
       1. The length of BC. (2 marks)
       2. The length of AC. (3 marks)
       3. The size of angle ACD. (3 marks)
24. The equation of a curve is y = -¹/₃x³ + 3x² - 5x + 5¹/₃
    1. Determine:
       1. The y – intercept of the curve. (1 mark)
       2. The stationary points of the curve. (4 marks)
       3. The nature of the stationary points in (a) (ii) above. (2 marks)
    2. On the space provided below, sketch the curve y = -¹/₃x³ + 3x² - 5x + 5¹/₃ showing clearly the y – intercept and the stationary points. (3 marks)