Mathematics Paper 2 Questions - Alliance Boys High School Post Mock KCSE 2020

Instructions to candidates

1. Write your name and index number admission number and class in the spaces provided above.
2. The paper contains TWO sections: Section I and Section II.
3. Answer ALL the questions in Section I and ANY FIVE questions from Section II
4. All answers and working must be written on the question paper in the spaces provided below each question.
5. Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
6. Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.

SECTION I

1. If 4x² + 32x-20+k is a perfect square, Find the value of k. (3 marks)
2. Find the sum to 20 terms of the series
   Log2 + Log 4+ Log 8 + Log 16+......(3marks)
3. Without using calculators or mathematical tables simplify(3marks)
   √63 + √72
   √32 + √28 
4. Solve for x in the equation.(3marks)
   log_x 64 – 1og₄  1  = 0
         27            64
5. A shear parallel to the x-axis maps (1,2) onto point (5,2)
   1. Determine the shear factor. (2marks)
   2. Hence state the shear matrix. (1mark)
6. Solve 2 sin²x - 3 sin x + 1 = 0 for 0° ≤ x ≤ 360° (4marks)
7. A curve is given by the equation y=5x³ - 7x² + 3x + 2. Find the equation of the normal to the curve at the point (1,3). (3marks)
8. Two variables P and Q are such that P varies partly as Q and partly as the square root of Q.
   Determine the relationship between P and Q. When Q=36, P=204 and when Q = 25 P=145. (4marks)
9. From a reservoir, water flows through a cylindrical pipe of diameter 0.2m at a rate of 0.35m/s.
   Determine the number of litres of water discharged from the reservoir in one hour. (3 marks)
10. Make the subject of the formula. (3marks)
    x= √k + a
          √k - b
11. A point P divides the line RT in the ratio -2:5. Find the coordinates of P given R (3, 1) and T (6,-5) (3marks)
12. Find the percentage error in finding the area of a rectangle whose measurements are 26.0cm and 14.2cm (3marks)
13. Patrick pays a car on hire purchase in 15 monthly installments. If the cash price of the car is Ksh. 300,000 and the interest rate is 12% per annum and he has to pay a down payment of ksh.75,000. Calculate his monthly repayments. (3marks)
14. The table below shows the income tax for a certain year
    

    Monthly taxable income	Tax rates (%)
    1-9680	10
    9681-18800	15
    18801-27920	20
    29921-37040	25
    37940 and above	30

    Hassan paid a gross tax of Ksh 3836 in a certain month. Calculate his monthly taxable income in ksh (3 marks)
15. Two matrices A and B are A = 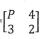and B = 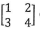. Given that the product AB has no inverse, find the value of P.
16. Draw the locus of the points that satisfy inequalities (y -3)² + (x - 2)² ≤ 9 and x + y ≥ 6 and shade the wanted region (3 marks)
    
    
    SECTION II
17. The figure below shows a frustum ABCDEFGH of a right pyramid such that AB =9cm, BC = 12cm, FG=6cm GH8cm and the height of the frustum is 10cm.
    
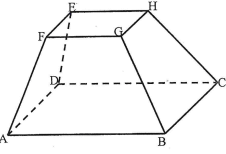
    Find the
    1. Height of pyramid (2 Marks)
    2. Length of
       1. AC (2 Marks)
       2. AH (2 Marks)
    3. Calculate the angle between:
       1. Line AH and the plane ABCD (2 Marks)
       2. The planes ABHE and ABCD (2 Marks)
18.  
    1. Complete the table below for y=sin 2x and y = sin (2x + 30) (2 marks)
       

       X	0	15	30	45	60	75	90	105	120	135	150	165	180
       Sin 2x	0				0.87				-0.87				0
       Sin ( 2x + 30)	0.5				0.5				-1				0.5

    2. Draw the graphs of yesin 2x and y=sin (2x + 30) on the axis. (4marks)
       
    3. Use the graph to solve sin (2x +30)-sin 2x = 0 (Imark)
    4. Determine the transformation which maps sin 2x onto sin (2x + 30) (1mark)
    5. State the period and the amplitude of y = sin ( 2x + 30) (2 marks)
19. The positions of three ports in the Indian Ocean are p (40°N, 30°W) Q(40°N, 20°E) and R (36's, 30°W) respectively.
    1. Find the distance in nautical miles to the nearest nm between:
       1. Ports P and Q (3 Marks)
       2. Ports P and R (2 Marks)
    2. A ship left port P on Tuesday 1430 hours and sailed to port Q at 20 knots.
       Calculate:
       1. The local time at port when the ship left port P (2 Marks)
       2. The day and time the ship arrived at port (3 Marks)
20. The following table shows the distribution of marks obtained by 50 students.
    

    Marks	45-49	50-54	55-59	60-64	65-69	70-74	75-79
    No of Students	3	9	13	15	5	4	1

    1. By using an assumed mean of 62, calculate:
       1. The actual mean.(4marks)
    2. The standard deviation (3marks)
    3. The quartile deviation (3 marks)
21. In the figure below O is the centre of the circle. Angle SPQ = 53 and angle PQO = 30°.
    
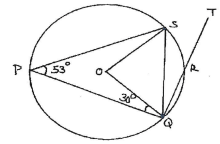
    1. Giving reasons find the size of angles:
       1. SOQ (2 marks)
       2. PSO.(2 marks)
       3. SRT(2 marks)
    2. If QS =14cm, find the area of the quadrilateral OQPS. (4 marks)
22. Every evening before the end of preps, Yoshi either reads a novel or solves a mathematical problem. The probability that he reads a novel is ⁴/₅. If he read a novel, there is a probability of ³/₄ that he will fall asleep. If he solves a mathematical problem, there is a probability of ¼ that he will fall asleep. Sometimes the teacher on duty enters Yoshi's classroom. When Yoshi is asked whether he had been asleep, there is a probability of only ¹/₅ that he will admit that he had been asleep and a probability of ³/₅ that he will claim to have been asleep when he had not been asleep By use of a tree diagram, find the probability that
    1. he sleeps and admits(4 marks)
    2. he sleeps and does not admit(2 marks)
       1. he does not sleep but claims that she had been asleep(2 marks)
       2. he does not sleep and says that she has not been asleep(2 marks)
23. The figure below shows parts of a curve whose gradient function is given by 3x - 6
    
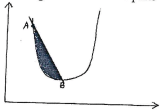
    Given that the curve passes through the points A(1,6) and has a minimum turning point at B
    Determine:
    1. The equation of the curve (3 marks)
    2. The coordinates of B(3 marks)
    3. The shaded region is bounded by the curve and the straight line passing through A and B, Calculate the area of the shaded region.(4 marks)
24. A farmer wishes to keep some chicks and ducks. Chicks cost Ksh. 60 each while ducks costs
    kshs. 80 each. She finds its uneconomical to keep less than 250 birds. She also wishes to keep more chicks than ducks but the chicks must be less than 200. She cannot afford to spend more than ksh. 24,000.
    1. Taking x and y to be the number of chicks and ducks respectively rite down all the inequalities that satisfy the above conditions.(4 marks)
    2. Represent the inequalities graphically shading out the unwanted region.(4 marks)
       
    3. If the farmer makes a profit of ksh. 200 per chicks and ksh 250 per duck, find the number of chicks and ducks she must keep in order to maximize her profit. and calculate the profit(2 marks)