INSTRUCTIONS TO CANDIDATES
- Write your name and Index number in the spaces provided at the top of this page.
- This paper consists of two sections: Section I and Section II.
- Answer ALL questions from section I and ANY FIVE from section II
- All answers and workings must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculation, giving your answer at each stage in the spaces below each question.
- Non – Programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise.
FOR EXAMINERS USE ONLY
SECTION I
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
TOTAL |
SECTION II
|
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
TOTAL |
|
|
|
|
|
|
GRAND TOTAL ...............
QUESTIONS
SECTION I (50 marks)
ATTEMPT ALL THE QUESTIONS IN THIS SECTION
- On average, the rate of depression of a water pump is 9% per annum. After three complete years it was Kshs. 150,700. Find its value at the start of the three years period. (3 marks)
- John truncated 7/9 to 3 decimal places. Calculate the percentage error resulting from the truncating. (3marks)
- Solve the equation4 sin2Ө + 4 cos Ө = 5 for 0o ≤ Ө ≤ 360o Give your answer in degrees. (3marks)
- The first term of an arithmetic sequence is (2x+1) and the common difference is (x+1) if the product of the first and the second terms is zero, find the first three terms of the two possible sequences. (3marks)
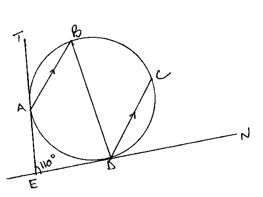
- TAE and EDN are tangents to a circle at A and D respectively. Line AB and DC are parallel chords; BD is another chord of the circle. Angle TAB is 46º. Find angle CDN giving reasons. (3 marks)
- Use logarithm table to evaluate. (4marks)
-
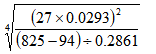
- Find the expansion of
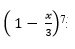in ascending powers of x up to the term in x2 (1mark) - Use the expansion above to find (0.99)7to four significant figures (2marks)
- Find the expansion of
- P and Q are the points on the ends of the diameter of the circle below.
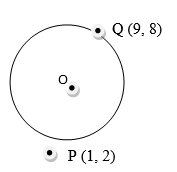
- Write down in terms of X and Y the equation of the circle in the form:
ax2 + by2 + x + y + c = 0 (2 marks) - Find the equation of the tangent at Q in the form ax + by + c = 0 (2 marks)
- Write down in terms of X and Y the equation of the circle in the form:
- Given that (OA) → = 3i +2j – 4k and (OB)→ = 4i+5j-2k and that p divides AB in the ratio 3: -2, determine the position vector of p in terms of i, j and k (3marks)
- The masses to the nearest kg of 50 adults were recorded as follows:
Calculate the quartile deviation. (3marks)Mass (kg)
Frequency (f)
45-50
2
51-56
10
57-62
11
63-68
20
69-74
6
75-80
1
- Machine A can complete a piece of work in 6 hours while machine B can complete the same work in 10 hours. If both machines start working together and machine A breaks down after two hours, how long will it take machine B to complete the rest of the work. (3marks)
- Without using tables, rationalize the denominator in
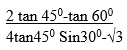(3 marks) - Make n the subject of the formula
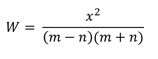(3 marks) - In a transformation, an object with area 9cm2 is mapped onto an image whose area is 54cm2. Given that the matrix of transformation is
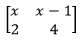find the value of x (3marks) - P varies as the cube of Q and inversely as the square root of R. If Q is increased by 20% and R decreased by 36%, find the percentage change in P. (3marks)
- An arc subtends an angle of 0.9 radians. If radius of circle is 13cm, find the length of the arc. (3 marks)
SECTION II (50 MARKS)
(ANSWER ANY FIVE QUESTIONS FROM THIS SECTION)
- The table below shows the Kenya tax rates in a year
In that year, Ushuru earned a basic salary of Ksh 30000 per month. In addition, he was entitled to a medical allowance of Ksh 2,800 per month and a traveling allowance of Ksh 1800 per month. He is housed by the employer and pays a nominal rent of 2000. He also claimed a monthly family relief of Ksh 1056. Other monthly deductions were union dues Ksh 445, WCPS Ksh 490, NHIF Ksh 320, COOP shares Ksh 1000 and risk fund Ksh 100Income (Ksh per annum)
Tax rate (per £)
1 – 116,160
10%
116,161 – 225,600
15%
225,601 – 335,040
20%
335,041 – 444,480
25%
Over 444,481
30%
Calculate:- Ushuru’s annual taxable income. (2marks)
- The tax paid by Ushuru in that year. (5marks)
- Ushuru’s net income in that year (3marks)
- The masses of 50 loaves of bread were taken and recorded as in the table blow.
Mass (gms)
470-479
480-489
490-499
500-509
510-519
520-529
530-539
No. of loaves
1
3
11
21
8
4
2
- Using an assumed mean of 504.5, calculate the mean mass (3marks).
- Calculate the
- Variance. (4marks)
- Calculate the standard deviation. (2marks)
- If 5 is added to each score and then divided by 3, write down the new standard deviation. (1mark)
- In chemistry form 4 classes, 1/3 of the class are girls and the rest boys, 4/5 of the boys and 9/10 of the girls are right handed while the rest are left handed. The probability that a right-handed student breaks a conical flask in any practical session is 3/10 and the corresponding probability of a left-handed student 4/10 . The probabilities are independent of the students gender.
- Represent the above information on a tree diagram with independent probabilities. (2 marks)
- Determine the probability that student chosen at random form the class is left handed and does not break a conical flask in simplest form. (3 marks)
- Determine the probability that a conical flask is broken in any chemistry practical session in simplest form. (3 marks)
- Determine the probability that a conical flask is not broken by a right-handed student in the simplest form. (2 marks)
- The roof of a ware house is in the shape of a triangular prism as shown below
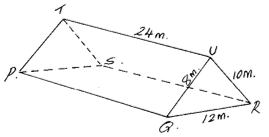
Calculate- The angle between faces RSTU and PQRS (3marks)
- The space occupied by the roof (3marks)
- The angle between the plane QTR and PQRS (4marks)
- A plane leaves an airport A (41.5ºN, 36.4ºW) at 9:00am and flies due north to airport B on latitude 53.2ºN. Taking π as 22/7 and the radius of the earth as 6370Km,
- Calculate the distance covered by the plane in km (4marks)
- The plane stopped for 30minutes to refuel at B and flew due east to C, 2500km from B. Calculate:
- position of C (3marks)
- The time the plane lands at C if its speed is 500km/h (3marks)
-
- Complete the table below giving your values correct to 2 d.p. (2marks)
x
00
150
300
450
600
750
900
1050
1200
3cos x0
3.00
2.60
1.50
0
-0.78
4sin(2x -100)
1.37
3.94
3.76
0.69
-3.06
- Draw the graphs of y = 3cos x0 and y = 4sin(2x- 100) on the same set of axis on the grid provided. (4marks)
- Use your graph to find values of x for which 3cosx – 4 sin (2x -100) = 0. (2marks)
- State
- The amplitude of the graph y = 3cos x. (1mark)
- The period of the graph y = 4sin (2x - 10º). (1mark)
- Complete the table below giving your values correct to 2 d.p. (2marks)
-
- Using a ruler, a pair of compasses only construct triangle XYZ such that XY = 6cm,
YZ = 8cm and ∠XYZ = 75º (3marks) - Measure
- line XZ (1mark)
- ∠XZY (1mark)
- Draw a circle that passes through X, Y and Z. (2marks)
- A point M moves such that it is always equidistant from Y and Z. Construct the locus of M and define the locus (3marks)
- Using a ruler, a pair of compasses only construct triangle XYZ such that XY = 6cm,
- A manager wishes to hire two types of machines. He considers the following facts.
He has a maximum of 24m2 of floor space and a maximum of 36 men available. In addition he is not allowed to hire more machines of type B than of type A.Machine A
Machine B
Floor space
2m2
2m2
Number of operators
4
3
- If he hires x machines of type A and y machines of type b write down all the inequalities that satisfy the above conditions. (3marks)
- Represent the inequalities on the grid and shade the unwanted region. (3marks)
- If the profit from machine A is sh. 4 per hour and that from using machine B is ksh. 8 per hour. What number of machines of each type should the manager choose to give the maximum profit. (4marks)
MARKING SCHEME
SECTION I (50 marks)
ATTEMPT ALL THE QUESTIONS IN THIS SECTION
- On average, the rate of depression of a water pump is 9% per annum. After three complete years it was Kshs. 150,700. Find its value at the start of the three years period. (3 marks)
A = P (1 - r )n
100
150,700 = P (1 - 9 )3
100
150,700 = P(0.91)3
P = 150,700
(0.091)3
P = 199981.16 - John truncated 7/9 to 3 decimal places. Calculate the percentage error resulting from the truncating. (3marks)
7 = 0.77777.............
9
trancating to 3 d.p 0.777 = 777
1000
absolute error = 7/9 - 777/1000 = 7/9000
% error = (7/9000 ÷ 7/9) × 100%
= 0.1% - Solve the equation 4 sin2Ө + 4 cos Ө = 5 for 0o ≤ Ө ≤ 360º Give your answer in degrees. (3marks)
4 sin2Ө + 4 cos Ө = 5 = 0
4(1 - cos2Ө) + 4 cos Ө - 5 = 0
4 - 4cos2Ө + 4cosӨ - 5 = 0
-4cos2Ө + 4cosӨ - 1 = 0
4cos2Ө - 4cosӨ + 1 = 0
(4cos2Ө - 2 cosӨ) - (2cosӨ + 1) = 0
(2 cosӨ - 1)(2 cosӨ - 1) = 0
2cosӨ - 1 = 0
cosӨ = 1/2
Ө = 60º, 300º both A1 - The first term of an arithmetic sequence is (2x+1) and the common difference is (x+1) if the product of the first and the second terms is zero, find the first three terms of the two possible sequences. (3marks)
a = 2x + 1
d = x + 1
t1 = 2x + 1
t2 = (2x + 1) + (x + 1)
= 3x + 2
m1 for both terms
(2x + 1)(3x + 2) = 0
2x + 1 = 0
x = 1/2
or
3x + 2 = 0
x = 2/3 - TAE and EDN are tangents to a circle at A and D respectively. Line AB and DC are parallel chords; BD is another chord of the circle. Angle TAB is 46º. Find angle CDN giving reasons. (3 marks)
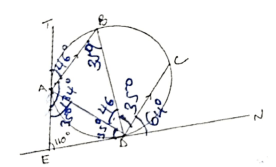
∠ADB = 46º
∠BDC = 35º
∠CDN = 64º
Award all marks if angles are shown on diagrams - Use logarithm table to evaluate. (4marks)
-
- Find the expansion of 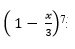in ascending powers of x up to the term in x2 (1mark)
(1 - x/3)7 = 1.17(-x/3)º + 7.16(-x/3)1 + 21.15(-x/3)2
= 1 - 7/3x + 7/3x2 - Use the expansion above to find (0.99)7to four significant figures (2marks)
(1 - x)7 = (1 - 0.01)7
3
x/3 = 0.01
x = 0.03
(0.99)7 = 1 - 7/3(0.003) + 7/3(0.03)2
=1 - 0.07 + 0021
= 0.9321
- Find the expansion of
- P and Q are the points on the ends of the diameter of the circle below.
- Write down in terms of X and Y the equation of the circle in the form:
ax2 + by2 + x + y + c = 0 (2 marks)
diameter = √(9 - 1)2 + (8 - 2)2
= √100
= 10 units
r = 5 units
center = (9 + 1, 8 + 2)
2 2
c(5,5)
(x - 5)2 + (y - 5)2 = 52
x2 - 10x + y2 - 10y + 25 = 0 - Find the equation of the tangent at Q in the form ax + by + c = 0 (2 marks)
gradient of diameter = 3 = (8 - 2)
4 ( 9 - 1)
grafient of tangent = -4/3
y - 8 = -4
x - 9 3
4x + 3y - 60 = 0
4x + 3y - 60 = 0
- Write down in terms of X and Y the equation of the circle in the form:
- Given that (OA) → = 3i +2j – 4k and (OB)→ = 4i+5j-2k and that p divides AB in the ratio 3: -2, determine the position vector of p in terms of i, j and k (3marks)
- The masses to the nearest kg of 50 adults were recorded as follows:
Calculate the quartile deviation. (3marks)Mass (kg)
Frequency (f)
c.f 45-50
2
2 51-56
10
12 57-62
11
23 63-68
20
43 69-74
6
49 75-80
1
50
lower quartile ¼ × 50 = 12.5 th
Q1
56.5 + (12.5 - 12) × 6
11
= 56.77 kg
upper quartile = ¾ × 50 = 37th
Q3
62.5 + (37.5 - 23) × 6
20
= 66.85kg
quartile deviation
= ½ × (66.85 - 56.77)
=5.04 - Machine A can complete a piece of work in 6 hours while machine B can complete the same work in 10 hours. If both machines start working together and machine A breaks down after two hours, how long will it take machine B to complete the rest of the work. (3marks)
both in 1 hr = 1/10 + 1/6 = 4/15
both in 2 hours = 2 × 4/15 = 8/15
remaining work = 1 - 8/15 = 7/15
if 1/6 = 1 hr
7/15 = 7/15 × 1 × 6 = 14/5 = 24/5 hrs
2 hrs 48min - Without using tables, rationalize the denominator in 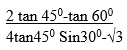(3 marks)
(2)1 - √3
4(1)(½) - √3
2 - √3
2 -√3
OR
2 - √3 × 2 + √3
2 - √3 2 + √3
4 + 2√3 - 2√3 - 3
4 + 2√3 - 2√3 - 3
= 1 - Make n the subject of the formula 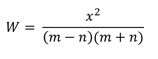(3 marks)
W = x2
m2 - n2
w = (m2 - n2) = x2
wm2 - wn2 = x2
wm2 - x2 = wn2
n2 = wm2 - x2
w
n = ±√wm2 - x2
w
or
n = ±√x2 - wm2
-w
zero marks if ± is missing - In a transformation, an object with area 9cm2 is mapped onto an image whose area is 54cm2. Given that the matrix of transformation is 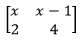find the value of x (3marks)
det = 4(x) - 2(x - 1)
= 4x - 2x + 2
= 2x + 2
det = Aimage
Aobject
= 54 = 6
9
6 = 2x + 2
4 = 2x
2 = x - P varies as the cube of Q and inversely as the square root of R. If Q is increased by 20% and R decreased by 36%, find the percentage change in P. (3marks)
*Accept alt methods
p = KQ3
√R
P1 = K(1.2Q)3
√0.64R
= 1.728KQ3
0.8√R
P1 = 2.16KQ3
√R
% change in p = (p1 - p) × 100%
p
= 2.16 - 1 × 100%
1
= 116% - An arc subtends an angle of 0.9 radians. If radius of circle is 13cm, find the length of the arc. (3 marks)
1º = 57.3º
0.9º = 51.57º
L = Ò 2πr
360
= 51.57 × 2 × 22 × 13
360 7
= 11.71cm
SECTION II (50 MARKS)
(ANSWER ANY FIVE QUESTIONS FROM THIS SECTION)
- The table below shows the Kenya tax rates in a year
In that year, Ushuru earned a basic salary of Ksh 30000 per month. In addition, he was entitled to a medical allowance of Ksh 2,800 per month and a traveling allowance of Ksh 1800 per month. He is housed by the employer and pays a nominal rent of 2000. He also claimed a monthly family relief of Ksh 1056. Other monthly deductions were union dues Ksh 445, WCPS Ksh 490, NHIF Ksh 320, COOP shares Ksh 1000 and risk fund Ksh 100Income (Ksh per annum)
Tax rate (per £)
1 – 116,160
10%
116,161 – 225,600
15%
225,601 – 335,040
20%
335,041 – 444,480
25%
Over 444,481
30%
Calculate:- Ushuru’s annual taxable income. (2marks)
T.income = sh 30000 + (15/100 × 30000) + 2800 + 1800 - 2000
= sh. 37100 - The tax paid by Ushuru in that year. (5marks)
1st 116160 × 0.1 = 11616
2nd 109440 × 0.15 = 16416
3rd 109440 × 0.20 = 21880
4th 109440 × 0.25 = 27360
removing 720 × 0.30 = 216
77488
net tax = 77488 - 12672 = sh 64816 - Ushuru’s net income in that year (3marks)
total deductions 5401.33 + 445 + 490 + 320 + 1000 + 100 = 7756.33
accept alternative
net salary per month 34600 - 7756.33
=sh. 26843.67
net salary p.a = sh.322124.04
- Ushuru’s annual taxable income. (2marks)
- The masses of 50 loaves of bread were taken and recorded as in the table blow.
Mass (gms)
470-479
480-489
490-499
500-509
510-519
520-529
530-539
No. of loaves
1
3
11
21
8
4
2
- Using an assumed mean of 504.5, calculate the mean mass (3marks).
mass class x f d. x - 504.5 d2 fd fd2 470-479 474.5 1 -30 900 -30 900 480-489 484.5 3 -20 400 -60 1200 490-499 494.5 11 -10 100 -110 1100 500-509 504.5 21 0 0 0 0 510-519 514.5 8 10 100 80 800 520-529 524.5 4 20 400 80 1600 530-539 534.5 2 30 900 60 1800 Σf = 50 Σfd = 20 Σfd2 = 7400 x = A + Σfd
Σf
x = 504.5 + 20
50
=504.9 - Calculate the
- Variance. (4marks)
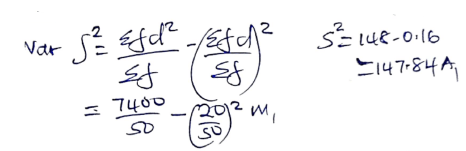
- Calculate the standard deviation. (2marks)
s = √147.84
= 12.16
- Variance. (4marks)
- If 5 is added to each score and then divided by 3, write down the new standard deviation. (1mark)
s = 12.16 = 4.053
3
- Using an assumed mean of 504.5, calculate the mean mass (3marks).
- In chemistry form 4 classes, 1/3 of the class are girls and the rest boys, 4/5 of the boys and 9/10 of the girls are right handed while the rest are left handed. The probability that a right-handed student breaks a conical flask in any practical session is 3/10 and the corresponding probability of a left-handed student 4/10 . The probabilities are independent of the students gender.
- Represent the above information on a tree diagram with independent probabilities. (2 marks)
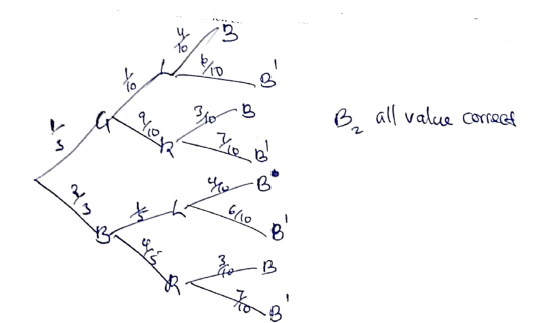
- Determine the probability that student chosen at random form the class is left handed and does not break a conical flask in simplest form. (3 marks)
p(glb) or p(blb)
= (1/3 × 1/10 × 6/10) + (2/3 × 1/5 × 6/10)
6/300 + 12/150 = 30/300 = 1/10 - Determine the probability that a conical flask is broken in any chemistry practical session in simplest form. (3 marks)
p(glb) or p(grb) or p(blb) or p(brb)
(1/3 × 1/10 × 4/10) + (1/3 × 9/10 × 3/10) + (2/3 × 1/5 × 4/10) + (2/3 × 4/5 × 3/10)
4/300 + 27/300 + 8/150 + 24/150 = 19/60 - Determine the probability that a conical flask is not broken by a right-handed student in the simplest form. (2 marks)
p(grb) or p(brb)
(1/3 × 9/10 × 9/10) + (2/3 × 4/5 × 7/10) = 175/300 = 7/12
- Represent the above information on a tree diagram with independent probabilities. (2 marks)
- The roof of a ware house is in the shape of a triangular prism as shown below
Calculate- The angle between faces RSTU and PQRS (3marks)
82 = 122 + 102 - 2(12)(10)cosR
64 = 144 + 100 - 240cosR
-180 = -240cosR
0.75 = cosR
41.41º = R - The space occupied by the roof (3marks)
volume = cross section area × length
= 1/2 × 12 × 10sin 41.41 × 24
= 952.48cm3 - The angle between the plane QTR and PQRS (4marks)
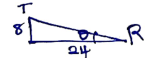
Tan σ = 8
24
σ = 18.43º
- The angle between faces RSTU and PQRS (3marks)
- A plane leaves an airport A (41.5ºN, 36.4ºW) at 9:00am and flies due north to airport B on latitude 53.2ºN. Taking π as 22/7 and the radius of the earth as 6370Km,
- Calculate the distance covered by the plane in km (4marks)
53.2 - 41.5 = 11.7º
dist = 11.7 × 2 × 22 × 6370
360 7
=1301.3 km - The plane stopped for 30minutes to refuel at B and flew due east to C, 2500km from B. Calculate:
- position of C (3marks)
σ × 2 × 22 × 6370cos53.2 = 2500km
360 7
σ = 37.5º
longitude = 37.5º - 36.4º = 1.1º
Z(53.2Nº, 1.1ºE) - The time the plane lands at C if its speed is 500km/h (3marks)
Time = 1301.3 + 1 + 2500
500 2 500
= 8 hours 6 minutes
37.5 × 4 = 150 min = 2hrs 30min
9.00 + 2hrs 30 min + 8hrs 6 min
= 7.36pm
- position of C (3marks)
- Calculate the distance covered by the plane in km (4marks)
-
- Complete the table below giving your values correct to 2 d.p. (2marks)
x
00
150
300
450
600
750
900
1050
1200
3cos x0
3.00
2.60
1.50
0
-0.78
4sin(2x -100)
1.37
3.94
3.76
0.69
-3.06
- Draw the graphs of y = 3cos x0 and y = 4sin(2x- 100) on the same set of axis on the grid provided. (4marks)
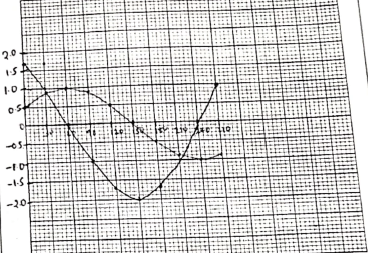
- Use your graph to find values of x for which 3cosx – 4 sin (2x -100) = 0. (2marks)
period 360 300
amount 1 2 - State
- The amplitude of the graph y = 3cos x. (1mark)
- The period of the graph y = 4sin (2x - 10º). (1mark)
- Complete the table below giving your values correct to 2 d.p. (2marks)
-
- Using a ruler, a pair of compasses only construct triangle XYZ such that XY = 6cm,
YZ = 8cm and ∠XYZ = 75º (3marks)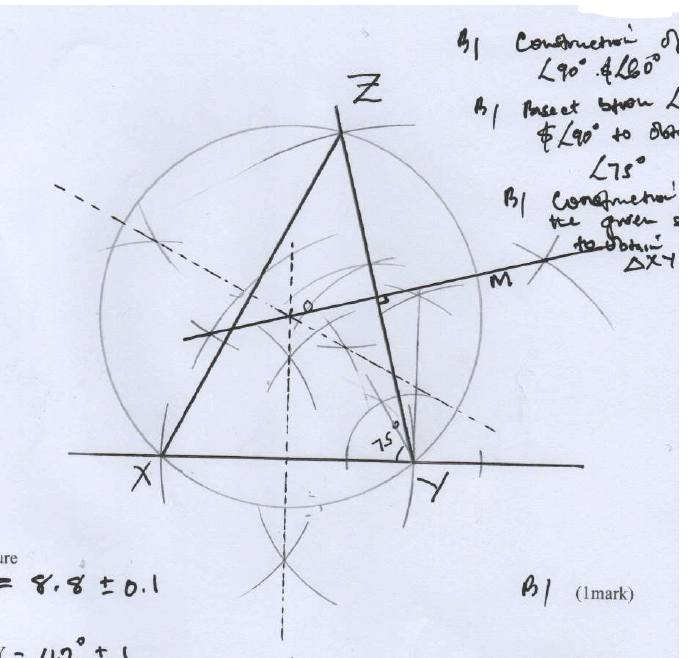
- Measure
- line XZ (1mark)
=8.8 ± 0.1 - ∠XZY (1mark)
= 42º ± 1
- line XZ (1mark)
- Draw a circle that passes through X, Y and Z. (2marks)
B1 - bisecting any 2 sides
B1 - circumference - A point M moves such that it is always equidistant from Y and Z. Construct the locus of M and define the locus (3marks)
m - perpendicular bisector of YZ B1(defining)
B1 bisecting
B1 indirecting the locus M
- Using a ruler, a pair of compasses only construct triangle XYZ such that XY = 6cm,
- A manager wishes to hire two types of machines. He considers the following facts.
He has a maximum of 24m2 of floor space and a maximum of 36 men available. In addition he is not allowed to hire more machines of type B than of type A.Machine A
Machine B
Floor space
2m2
2m2
Number of operators
4
3
- If he hires x machines of type A and y machines of type b write down all the inequalities that satisfy the above conditions. (3marks)
- Represent the inequalities on the grid and shade the unwanted region. (3marks)
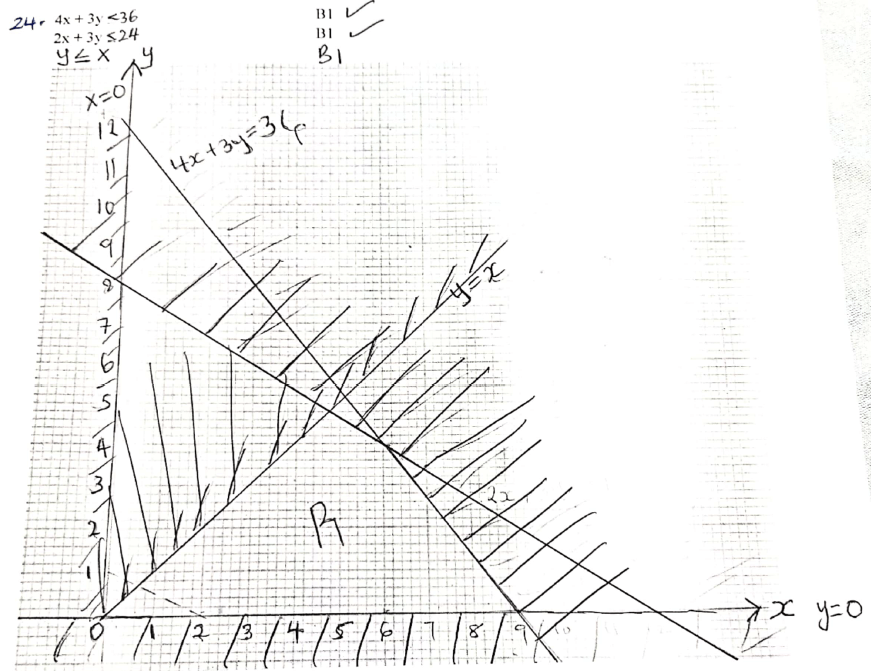
- If the profit from machine A is sh. 4 per hour and that from using machine B is ksh. 8 per hour. What number of machines of each type should the manager choose to give the maximum profit. (4marks)
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics P2 Questions and Answers - Butula Sub-County Post Mock Exams 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students
