INSTRUCTIONS TO CANDIDATES
- This paper consists of TWO sections: Section I and Section II.
- Answer ALL the questions in Section I and only five questions from Section II.
- All answers and workings must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
- Marks may be given for correct working even if the answer is wrong
- Non-programmable silent electronic calculators and KNEC Mathematical tables may be used, except where stated otherwise.
- This paper consists of 16 printed pages.
- Candidates should check the question paper to ascertain that all the pages are printed as indicted and that no questions are missing.

QUESTIONS
SECTION A (50 MARKS)
- Evaluate, (3 marks)
-12 ÷ (-3) x 4 – (-15)
-5 x 6 ÷ 2 + (-5) - A trader sold an article at 15% discount to a customer who paid sh.510 for it. What was the marked price of the article? (2 marks)
- Two similar cubes have masses of 512g and 125g. The base area of the larger cube is 64cm2. Find the base area of the smaller cube. (3 marks)
- Simplify, (3 marks)
16m2 - 9n2
4m2 - mm - 3n2 - The ratio of john’s earnings to muse’s earnings is 5:3. If john’s earnings increase by 12%, his new figure becomes sh. 5 600. Find the corresponding percentage change in muse’s earnings if the sum of their new earnings is sh.9 600. (4 marks)
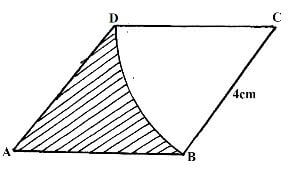
- The figure below is a rhombus ABCD of sides 4cm. BD is an arc of circle centre C. Given that ABC = 1380. Find the area of shaded region. (3 marks)
- A shopkeeper sells two- types of pangas type x and type y. Twelve x pangas and five type y pangas cost Kshs 1260, while nine type x pangas and fifteen type y pangas cost 1620. Mugala bought eighteen type y pangas. How much did he pay for them? (3 marks)
- During a certain month, the exchange rates in a bank were as follows;
A tourist left Kenya to the United States with Ksh.1 000,000.On the airport he exchanged all the money to dollars and spent 190 dollars on air ticket. While in US he spent 4500 dollars for upkeep and proceeded to Europe. While in Europe he spent a total of 2000 Euros. How many Euros did he remain with? (3marks)Buying (Ksh.)
Selling (Ksh.)
1 US $
91.65
91.80
1 Euro
103.75
103.93
- Using a ruler and a pair of compasses only,
- Construct a triangle ABC in which AB = 9cm, AC = 6cm and angle BAC = 37½º(2 marks)
- Drop a perpendicular from C to meet AB at D. Measure CD and hence find the area of the triangle ABC. (2 marks)
- Given that log 3 = 0.4771 and log 5 = 0.6990, without using logarithm tables or a calculator, evaluate log 0.135. (3 marks)
- The diagram below represents a right pyramid on a square base of side 3 cm. The slant height of the pyramid is 4 cm.
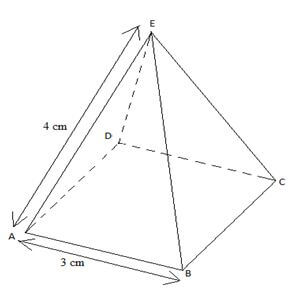
- Draw a net of the pyramid ( 3 marks)
- A translation maps a point (1, 2) onto (-2, 2). What would be the coordinates of the object whose image is (-3, -3) under the same translation? (3 marks)
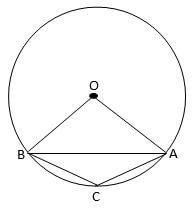
- In the figure below, O is the centre of the circle. Angle OAB = 300 and angle CAB = 230. Find angle ABC. (3 marks)
- The line which joins the point A (3,k) and B(-2,5) is parallel to the line whose equation is 5/7y + 2/7x = 1find the value of k. (3 marks)
- A segment is a region of a circle bounded by a chord and an arc.
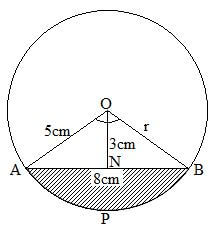
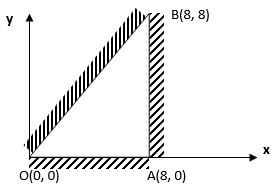
In the figure above the shaded region is a segment of the circle with Centre O and radius r. AB=8 cm, ON = 3 cm, Angle AOB = 106.3º. Find the area of the shaded part. (3 marks) - The vertices of the unshaded region in the figure below are O(0, 0) , B(8, 8) and A (8, 0). Write down the inequalities which satisfy the unshaded region. (3 marks)
SECTION B (50MKS)
- A straight line L1 has a gradient -1/2 and passes through point P (-1,3). Another line L2 passes through the points Q (1,-3) and R(4,5). find ,
- The equation of L1. (2 marks)
- The gradient of L2. (1 mark)
- The equation of L2. (2 marks)
- The equation of a line passing through a point S (0,5) and is perpendicular to L2. (3 marks)
- The equation of a line through R parallel to L1. (2 marks)
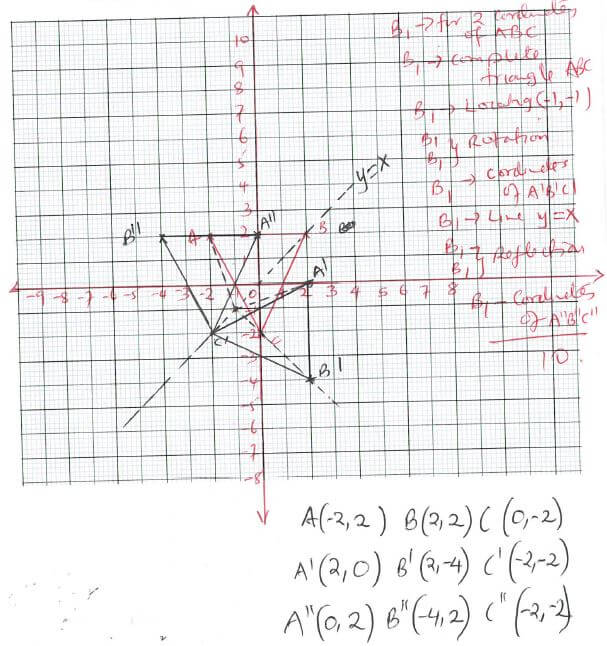
- A(-2,2), B(2,2) and C(0,-2) are coordinates of vertices of a triangle ABC;
- On the grid provided draw triangle ABC (2 marks)
- A’B’C’ are the images of ABC under a rotation 900 clockwise turn about (-1,-1). Find the coordinates of A’B’C’ on the same grid. (4 marks)
- ABC is reflected on the line y= x to form an image A’’B’’C’’. Find the image and the coordinates of A’’B’’C’’. (4 marks)

- The diagram represents a solid frustum with base radius 21cm and top radius 14cm.
The frustum is 22.5cm high and is made of a metal whose density is 3g/cm3 .
(Use π = 22/7).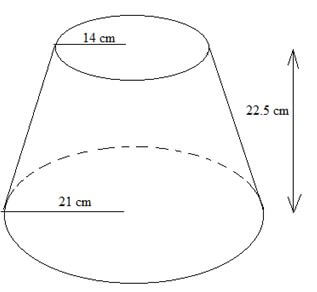
Calculate;- The volume of the metal in the frustum. (5 marks)
- The mass of the frustum in kg. (2 marks)
- The frustum is melted down and recast into a solid cube. In the process 20% of the metal is lost. Calculate to 2 decimal places the length of each side of the cube. (3 marks)
- The height of 36 students in a class was recorded to the nearest centimetres as follows.
148 159 163 158 166 155 155 179 158 155 171 172
156 161 160 165 157 165 175 173 172 178 159 168
160 167 147 168 172 157 165 154 170 157 162 173- Make a grouped frequency distribution table with 145.5 as lower class limit and class width of 5. (3 marks)
- Calculate the mean height of the students (3 marks)
- Draw a histogram to represent the above information on the grid provided . (4 marks)

- A train travelling between two stations starts from rest and accelerates uniformly for 150 seconds. It then travels at a constant speed for 300 seconds and finally decelerates uniformly for 200 seconds to rest. Given that the distance between the two stations is 10450m,
- Sketch the speed time graph for the train. (3 marks)
- Calculate; the maximum speed in km/h the train attained. (3 marks)
- Acceleration (2 marks)
- Distance the train travelled during the last 100 seconds (2 marks)
- Given that 4p - 3q =
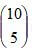 and p + 2q =
and p + 2q = 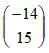 find
find-
- p and q (3 marks)
- |p + 2q| (3 marks)
- Show that A (1, -1), B (3, 5) and C (5, 11) are collinear. (4 marks)
-
- From town P, a town Q is 60km away on a bearing South 80º east. A third town R is 100km from P on the bearing South 40º west. A cyclist travelling at 20km/h leaves P for Q. He stays at Q for one hour and then continues to R. He stays at R for 1½ hrs. and then returns directly to P.
- Sketch the positions of towns PQR . (2 marks)
- Calculate the distance of Q from R. (3 marks)
- Calculate the bearing of R from Q. (3 marks)
- What is the time taken for the whole round trip? (2 marks)
- A particle moves in a straight line so that t seconds after passing affixed point in the line, its velocity v m/s is given by
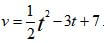 .
.- The velocity after 8s, (3 marks)
- The acceleration when t = 0 (2 marks)
- The minimum velocity (2 marks)
- The distance travelled in the first two seconds of motion, (3 marks)

MARKING SCHEME
SECTION A (50 MARKS)
- Evaluate, (3 marks)
-12 ÷ (-3) x 4 – (-15)
-5 x 6 ÷ 2 + (-5)
N= 4 x x 4 + 15 = 31
D = -15 - 5 = -20
31/20 = -111/20
=-1.55 - A trader sold an article at 15% discount to a customer who paid sh.510 for it. What was the marked price of the article? (2 marks)
100/85 x 510
=600 - Two similar cubes have masses of 512g and 125g. The base area of the larger cube is 64cm2. Find the base area of the smaller cube. (3 marks)
vsf = 512/125 -> L.S.F = √512/125 = 8/5 = 13/5
25/64 x 64 = 25cm2 - Simplify, (3 marks)
16m2 - 9n2
4m2 - mm - 3n2
N = (4m - 3n)(4m + 3n)
D: 4m2 - 4mn + 3mn - 3n2
= 4m(m - n) + 3n (m - n)
(4m - 3n)(4m + 3n) = 4m - 3n
(4m + 3n) (m - n) m - n - The ratio of john’s earnings to muse’s earnings is 5:3. If john’s earnings increase by 12%, his new figure becomes sh. 5 600. Find the corresponding percentage change in muse’s earnings if the sum of their new earnings is sh.9 600. (4 marks)
100/112 x 5600 = 5000
john = 5000
musa = 3/5 x 5000 = 3000
9600 - 5600 = 4000
4000 - 3000 x 100 = 331/3%
3000 - The figure below is a rhombus ABCD of sides 4cm. BD is an arc of circle centre C. Given that ABC = 1380. Find the area of shaded region. (3 marks)

area of rhombus
= (1/2 x 42 sin 42) + 1/2 x 42 sin 42
=10.71
Area of sector = 42/360 x 22/7 x 42
= 6.146
shaded area = 10.71 - 6.146
= 4.564 - A shopkeeper sells two- types of pangas type x and type y. Twelve x pangas and five type y pangas cost Kshs 1260, while nine type x pangas and fifteen type y pangas cost 1620. Mugala bought eighteen type y pangas. How much did he pay for them? (3 marks)
12x + 5y = 1260
9x + 15y = 1620
18 x x60 = 1080
36x + 15y = 3780
9x + 15y = 1620
27x = 2160
x = 80
9(80) + 15y = 1620
15y = 900
y = 60 - During a certain month, the exchange rates in a bank were as follows;
A tourist left Kenya to the United States with Ksh.1 000,000.On the airport he exchanged all the money to dollars and spent 190 dollars on air ticket. While in US he spent 4500 dollars for upkeep and proceeded to Europe. While in Europe he spent a total of 2000 Euros. How many Euros did he remain with? (3marks)Buying (Ksh.)
Selling (Ksh.)
1 US $
91.65
91.80
1 Euro
103.75
103.93
1,000,000 = 10,893.25 $
91.80 - 190.00
10,703.25
4,500.00
6,203.25
6,203.25 $ x 91.65
103.93
= 5470.30 euros
2000.00
3470.30 euros - Using a ruler and a pair of compasses only,
- Construct a triangle ABC in which AB = 9cm, AC = 6cm and angle BAC = 37½º(2 marks)
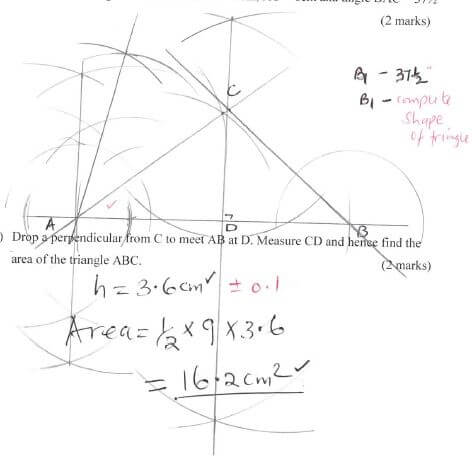
- Drop a perpendicular from C to meet AB at D. Measure CD and hence find the area of the triangle ABC. (2 marks)
- Construct a triangle ABC in which AB = 9cm, AC = 6cm and angle BAC = 37½º(2 marks)
- Given that log 3 = 0.4771 and log 5 = 0.6990, without using logarithm tables or a calculator, evaluate log 0.135. (3 marks)
0.135 = 135 = 33 x 5
1000 1000
log 0.135 = 3 log 3 + log 5 - log 1000
= 3 (0.4771) + 0.6990 - 3
= 2.1303 - 3.0000 = 1.1303 - The diagram below represents a right pyramid on a square base of side 3 cm. The slant height of the pyramid is 4 cm.

- Draw a net of the pyramid ( 3 marks)
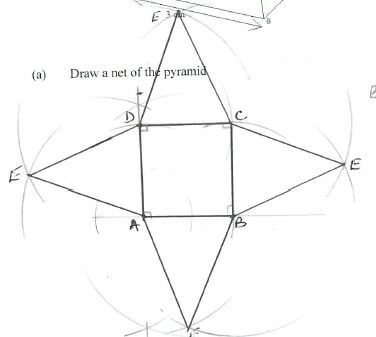
B1 -> square base
B1 - > 2 triangular faces
B1 - > 2 triangular faces
- Draw a net of the pyramid ( 3 marks)
- A translation maps a point (1, 2) onto (-2, 2). What would be the coordinates of the object whose image is (-3, -3) under the same translation? (3 marks)
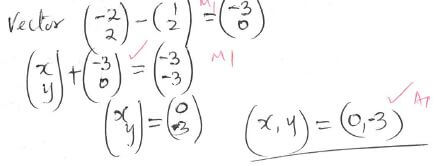
- In the figure below, O is the centre of the circle. Angle OAB = 300 and angle CAB = 230. Find angle ABC. (3 marks)
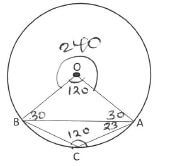
< BAC = 120º
<ABC = 180 - (120 + 23)
= 37º - The line which joins the point A (3,k) and B(-2,5) is parallel to the line whose equation is 5/7y + 2/7x = 1find the value of k. (3 marks)
5/7y = -2/7x + 1
y = -2/7 x 2/5x + 7/5
y = -2/5x + 1.4
5 - k = -2 -> 5 - k = -2
-2 - 3 5 -5
5/5(5 - k) = 10/5
5 - k = 2
k = 3 - A segment is a region of a circle bounded by a chord and an arc.

cos 53.15 = 3/r
r = 3/cos 53.15
= 5cm - In the figure above the shaded region is a segment of the circle with Centre O and radius r. AB=8 cm, ON = 3 cm, Angle AOB = 106.3º. Find the area of the shaded part. (3 marks)
area of sector = 1063 x 3.142 x 52 = 23.19
360
Area of triangle = 1/2 x 8 x 3 = 12
segment = 23.19 - 12 = 11.19cm - The vertices of the unshaded region in the figure below are O(0, 0) , B(8, 8) and A (8, 0). Write down the inequalities which satisfy the unshaded region. (3 marks)

x ≤ 8
y ≥ 0
y ≤ x
SECTION B (50MKS)
- A straight line L1 has a gradient -1/2 and passes through point P (-1,3). Another line L2 passes through the points Q (1,-3) and R(4,5). find ,
- The equation of L1. (2 marks)
y + 3 = -1
x + 1 2
2y + 6 = -x - 1
2y = -x - 2
y = -1/2x - 31/2 - The gradient of L2. (1 mark)
5 + 3 = 8
4 - 1 3
y + 3 = 8
x - 1 3 - The equation of L2. (2 marks)
y + 3 = 8
x - 1 3
3y = 8x - 17
y = 22/3x - 52/3 - The equation of a line passing through a point S (0,5) and is perpendicular to L2. (3 marks)
m2 = -3/8
y - 5 = -3/8
x
8y - 40 = -3x
8y + 3x = 40
y = -3/8x + 5 - The equation of a line through R parallel to L1. (2 marks)
y - 5 = -1/2
x - 4
2y - 10 = 4 - x
2y + x = 14
or
y = -1/2 + 7
- The equation of L1. (2 marks)
- A(-2,2), B(2,2) and C(0,-2) are coordinates of vertices of a triangle ABC;
- On the grid provided draw triangle ABC (2 marks)
- A’B’C’ are the images of ABC under a rotation 900 clockwise turn about (-1,-1). Find the coordinates of A’B’C’ on the same grid. (4 marks)
- ABC is reflected on the line y= x to form an image A’’B’’C’’. Find the image and the coordinates of A’’B’’C’’. (4 marks)
- The diagram represents a solid frustum with base radius 21cm and top radius 14cm.
The frustum is 22.5cm high and is made of a metal whose density is 3g/cm3 .
(Use π = 22/7).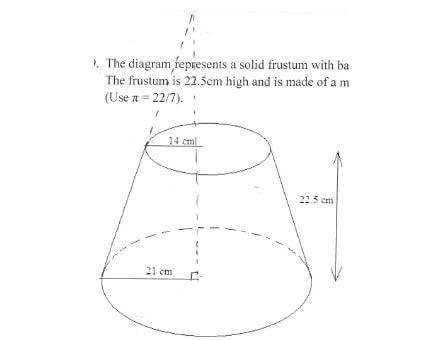
h + 22.5 = 21 = 3
h 14 2
2(h + 22.5) = 3h
2h + 45 = 3h
h = 45cm
Calculate;- The volume of the metal in the frustum. (5 marks)
1/3 x 22/7 x 212 x 67.5 = 31,185
1/3 x 22/7 x 142 x 45 = 9240
31,185 - 9240 = 21, 945cm3 - The mass of the frustum in kg. (2 marks)
m = vf = (21, 945 x 3) g = 65, 835g
= 65.835 kg - The frustum is melted down and recast into a solid cube. In the process 20% of the metal is lost. Calculate to 2 decimal places the length of each side of the cube. (3 marks)
80/100 x 21945 = L3 = 17,556
L = 3√17,556
=25.99
- The volume of the metal in the frustum. (5 marks)
- The height of 36 students in a class was recorded to the nearest centimetres as follows.
148 159 163 158 166 155 155 179 158 155 171 172
156 161 160 165 157 165 175 173 172 178 159 168
160 167 147 168 172 157 165 154 170 157 162 173- Make a grouped frequency distribution table with 145.5 as lower class limit and class width of 5. (3 marks)
∑xf = 5871Class Tally f x xf 146 - 150 II 2 148 296 151 - 155 IIII 4 153 612 156 - 160 IIIIIIIIIII 10 158 1580 161 - 165 IIIIII 6 162 976 166 - 170 IIIII 5 168 840 171 - 175 IIIIIII 7 173 1211 176 - 180 II 2 178 356 - Calculate the mean height of the students (3 marks)
x = 5871 = 163.08
36
=163.1 - Draw a histogram to represent the above information on the grid provided . (4 marks)
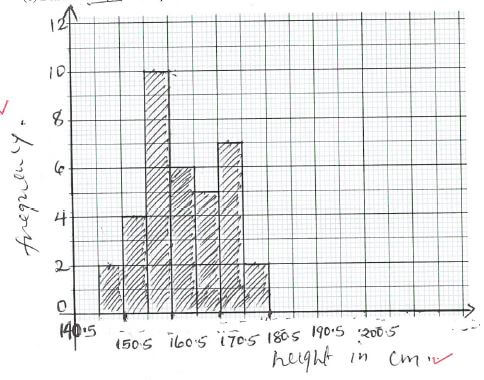
- Make a grouped frequency distribution table with 145.5 as lower class limit and class width of 5. (3 marks)
- A train travelling between two stations starts from rest and accelerates uniformly for 150 seconds. It then travels at a constant speed for 300 seconds and finally decelerates uniformly for 200 seconds to rest. Given that the distance between the two stations is 10450m,
- Sketch the speed time graph for the train. (3 marks)
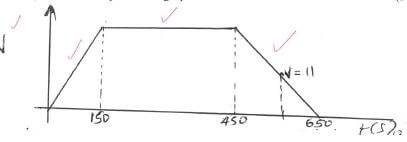
- Calculate; the maximum speed in km/h the train attained. (3 marks)
1/2 (650 + 300)v = 10450
950v = 20900
v = 22m/s
= 79.2km/h - Acceleration (2 marks)
22 -10 = 11
150 75
= 0.1467m/s2 - Distance the train travelled during the last 100 seconds (2 marks)
av velocity = 11m/s2
1/2 x 100 x 1 = 550
0 + 22 = 11
2
11 + 0 = 5.5 m/s
2
5.5 x 100 = 550m
- Sketch the speed time graph for the train. (3 marks)
- Given that 4p - 3q =
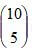 and p + 2q =
and p + 2q = 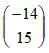 find
find-
- p and q (3 marks)
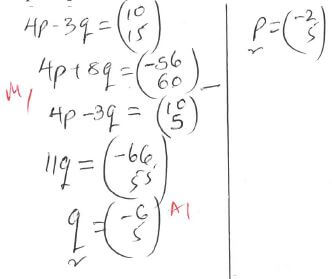
- |p + 2q| (3 marks)
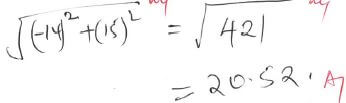
- p and q (3 marks)
- Show that A (1, -1), B (3, 5) and C (5, 11) are collinear. (4 marks)
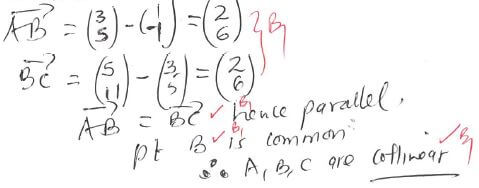
-
- From town P, a town Q is 60km away on a bearing South 80º east. A third town R is 100km from P on the bearing South 40º west. A cyclist travelling at 20km/h leaves P for Q. He stays at Q for one hour and then continues to R. He stays at R for 1½ hrs. and then returns directly to P.
- Sketch the positions of towns PQR . (2 marks)
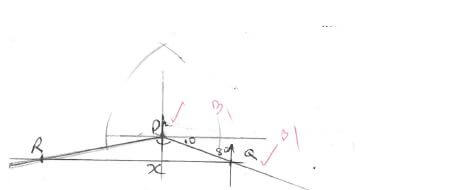
- Calculate the distance of Q from R. (3 marks)
x2 = 1002 + 602 - 2(60)(100) cos 160
= 13600 - - 11.276
=24,876
= √24, 876
=157.7km - Calculate the bearing of R from Q. (3 marks)
157.5 = 100
sin 160 sin Q
Sin R = 100 sin 160
157.5
=12.54º
80 + 12.5 = 92.5
360 - 92.5
- 267.5º - What is the time taken for the whole round trip? (2 marks)
66 + 157.7 + 100 = 317.7
317.7 = 15.885hrs = 15 hrs 53min
15 hr 33 min
+ 2 30
18 hr 03 min
- Sketch the positions of towns PQR . (2 marks)
- A particle moves in a straight line so that t seconds after passing affixed point in the line, its velocity v m/s is given by
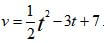 .
.- The velocity after 8s, (3 marks)
v = 1/2 (8)2 - 3(8) + 7
= 32 - 24 + 7
=15m/s - The acceleration when t = 0 (2 marks)
a = t - 3
= - 3m/s 2 - The minimum velocity (2 marks)
t - 3 = 0
t = 3
v= 1/2 (3)2 - 3(3) + 2
ans = 2.5m/s - The distance travelled in the first two seconds of motion, (3 marks)
ans = 91/3
- The velocity after 8s, (3 marks)
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Paper 1 Questions and Answers - Bunamfan Post Mock 2021 Exams.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

