INSTRUCTIONS TO CANDIDATES
- This paper consists of two sections: Section l and Section II
- Answer all questions in section l and Section II.
- Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non- programmable silent electronic calculators and KNEC Mathematical tables may be used.
SECTION I (40 MARKS)
ANSWER ALL QUESTIONS IN THIS SECTION
- Find the equation of a line through point (5, -1) and perpendicular to line 4x + 2y – 3 = 0. (3mks)
- Two spheres have surface areas of 36 cm2 and 49 cm2. If the volume of the smaller sphere is 20.2cm3. Calculate the volume of the larger one. (3 mks)
- Find the integral values of x which satisfy the following inequality.
6 – 3x ≤ 2x – 4 < x + 1 (3 marks) - Factorize the quadratic expression below: x2 + 6x + 9 (3mks)
- The interior angle of a regular polygon is 150o. Find the value of n. (3 mks)
- Simplify the following expression (3 mks)
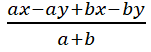
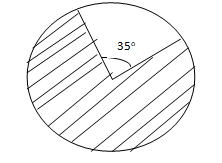
- Calculate the area of the shaded region given that the radius is 27cm. (4 mks)
- Simplify:(3 mks)
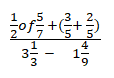
- Using a pair of compasses and a ruler only construct a triangle ABC such that AB= 4cm,
BC = 6cm and angle ABC = 135°. (3mks) - Calculate the volume of a sphere of radius 9cm. (3mks)
- Solve for x. If 32X+3 +1 = 28. (3mks)
- A straight line passing through A (-2,1) and B(2,-k). The line is perpendicular to a line 3y + 2x = 5. Determine the value of k and hence the equation passing through A and B. (3mks)
- Use substitution method to solve:
3y+2x=13
2y-3x=0
SECTION II (30 MARKS)
ANSWER ALL QUESTIONS IN THIS SECTION
- A soda depot had 30816 sodas which were packed in crates. Each crate contained 24 sodas. The mass of an empty crate was 2kg and that of a full crate is 12 kg.
- How many crates were there? (2mks)
- What was the total mass of empty crates? (2mks)
- What was the total mass of sodas alone? (3mks)
- A lorry was hired to transport the crates at a cost of sh. 5 per crate of soda per trip. The lorry could only carry 107 crates per trip. How much money was spent on transporting all the crates? (3mks)
- Triangle PQR has vertices P(3,2), Q(-1,1) and R(-3,-1).
- Draw PQR on the grid provided. (1mk)
- Under a rotation the vertices of P1Q1R1 are P1(1,4), Q1(2,0) and R1(4,-1). Find the centre and angle of rotation using points P and Q. (4mks)
- Triangle PQR is enlarged with scale factor 3 centre O(0,0) to give triangle P2Q2R2. Draw triangle P2Q2R2 and state its co-ordinates. (2mks)
- Triangle P1Q1R1 undergoes reflection in line y = x to give triangle P3Q3R3. Draw P3Q3R3 and state its coordinates. (3mks)
- A country bus left Nairobi at 10.45a.m and traveled towards Mombasa at an average speed of 60km/h. A matatu left Nairobi at 1:15p.m on the same day and traveled along the same road at an average speed of 100km/h. The distance between Nairobi and Mombasa is 500km.
- Determine the time of the day when the matatu overtook the bus (5mks)
- Both vehicles continued towards Mombasa at their original speeds. How long had the Matatu waited before the bus arrived? (5mks)

Marking Scheme
- 4x+2y-3=0
2y=-4+3
y=-2x+3
2
-2M2 = -1
M2=1
2
y-1= 1
x-5 2
2y+2=x-5
2y-x=-7 - Solution:
- 6 – 3x ≤ 2x – 4 < x + 1
6 – 3x ≤ 2x – 4
-5x ≤ -10
2 ≤ x
2x – 4 < x + 1
x < 5
2 ≤ x < 5 - x2 + 6x + 9 (3,3)
x2(x+3)+3(x+3)
(x+3)(x+3) - interior angles=150º
exterior angles= 30º
sum of all exterior angles= 360º
360º = 12
30º
=12 sides - ax-ay+bx-by
a+b
= a(x-y)+b(x-y)
a+b
= (a-b)(x-y)
a+b
= x-y - 360-35=325
325 x 27 x 27= 658.125cm2
360 - Answer:
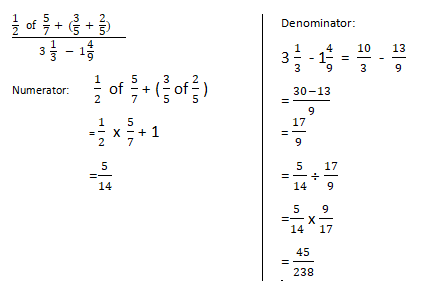
- .
- answer:
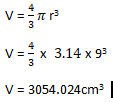
- 32x + 3 + 1 = 28
32x + 3 = 28 -1=27
32x + 3 = 3 3
2x + 3 = 3
2x = 0
x = 0 - 3y + 2x = 5
3y = -2x + 5
y = -2x + 5
3 3
gradient M1 = -2/3
M2 = 3/2
change in y = -k - 1 = 3
change in x 2 + 2 2
-k - 1 =3
4 2
-k - 1 = 3 x 4
2
-k -1 = 6
-k = 7
k= -7 - 3y + 2x = 13
2y - 3x = 0
2y = 3x
y = 3/2x
3(3/2x) + 2x = 13
9/2x + 2x =13
9x + 4x
2
13x = 13
2
x = 2. - .
- 30816 ÷ 24
= 1284 crates - 1284 x 2 = 25.68kg
- 12 - 2 = 10kg
10 x 1284 = 12840kg - 1204 ÷ 107 = 12 trips
5 x 107 = 535 per trip
12 x 535 = Ksh. 6420
- 30816 ÷ 24
- .
- .
- Time of day:
1:15pm - 10:45 am = 2 hours 30 minutes= 2.5 hrs
Distance= Speed x time
= 60km/h x 2.5 = 150km
Distance of overtaking means
distance for bus= distance for matatu
let distance that bus had covered when matatu left be x, then distance of bus that was covered will be 150+x
theerefore: x = 150+ x
60 100
100x = 9000 + 60x
100x - 60x = 9000
40x = 9000
x = 225 km
time for bus when overtaken = 225
60
= 3 hrs 45 minutes
1: 15
+ 3: 45
5:00
time = 5:00 pm - Distance remaining= 500 - 150 - 225 = 125km
Time taken by matatu: 125 = 1.25 hours = 1 hour 15 minutes
100
Time taken by bus: 125 = 2hours 5 minutes
60
time waited: 2: 05
-1: 15
: 50
= 50 minutes
- Time of day:
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Mathematics Questions and Answers - Form 2 End Term 3 Exams 2021.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students


