Mathematics Questions and Answers - Form 2 End of Term 3 Exams 2022

QUESTIONS

SECTION I:
Answer all questions.

1. Solve the following simultaneous equation (3mks)
   2x + 3y = 8
   5x – y = 3
2. The internal and external diameters of a spherical shell are 7cm and 14cm respectively. Calculate the volume of material of the shell. (3mks)
3. Use reciprocal tables and square root tables to evaluate: (3mks)
   1/3.953+√2.458
4. Evaluate without using a calculator (3mks)
   (-9+(-7)×(-8)-(-5))
      (-2+(-6)÷3×6)
5. Solve √1.843×0.048 using logarithm tables. (3mks)
                   11.53
6.                
   1. Find the gradient of the straight line passing through the points P (2,3) and Q (8,-6) (1mk)
   2. Hence find the equation of a line parallel to the straight line and passing through R (1,2) in the form of y=mx+c. (3mks)
7. The corresponding sides of two similar regular pentagons are 3cm and 7cm respectively. (3mks)
   1. Find the ratio of their areas.
   2. Calculate the area of the larger if the area of the smaller is 36cm².
8. A triangular flower garden measure 10m, 15m and 24m. Find the area of the garden. (3mks)
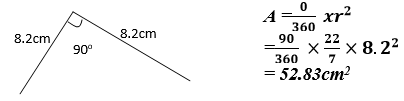
9. Two arms of a pair of divider are spread so that the angle between them is 90º. Find the area of the sector formed if the length of an arm is 8.2cm. (3mks)
10. Without using a calculator, evaluate; (3mks)
    (2 1⁄5+2⁄3 of3 3⁄4-4 1⁄6)
    (1 1⁄4-2 2⁄5 ÷1 1⁄3-3 3⁄4)
11. An observer stationed 20m away from a tall building finds that the angle of elevation of the top of the building is 68o and angle of its foot is 50o. Calculate the height of the building. (3mks)
12. Factorize the following; (2mks)
    4x² + 7x + 3
13. Find the integral values of the inequalities. (3mks)
    -1 ≤ 3x -1 < 5
14. Three years ago, Juma was three times as old. as Ali and in two years time, the sum of their ages will be 62. Determine their present ages (3mks)
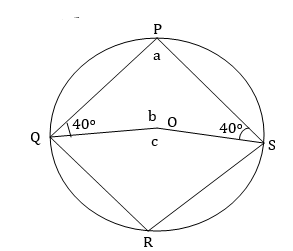
15. The figure below shows a circle with centre O. Find the values of a, b, c and if <PQO=40º, <PSO=30º (3mks)
    
16. A tourist visited Kenya with 2500 US dollars and changed the US dollars into Kenya shillings at a local bank in Kenya when the exchange rates at the time were as follows:
                                          Buying           Selling
    1 US dollar                   shs.78.45      shs. 78.55
    1 Sterling Pound          shs.120.25    shs. 120.45
    1. How much did he get in Kenya shillings? (2mks)
    2. While in Kenya he used shs. 80,000 and after his stay he converted the remaining amount into Sterling pounds. Calculate to 2 decimal places the Sterling pounds that he got (2mks)

SECTION II:
Answer any THREE Question.

17. The table below shows the names of 200 persons measured to the nearest kg
    

    Mass (kg)	40-49	50-59	60-69	70-79	80-89	90-99	100-109
    No. of persons	9	27	70	50	26	12	6

    1. State the modal class (1mk)
    2. Calculate the mean mass (5mks)
    3. Calculate the median mass (4mks)
18. Using a ruler and pair of compasses only.
    1. Construct a triangle ABC in which AB=9cm, AC=6cm and BAC=37 ½º. (5mks)
    2. Measure line BC (1mk)
    3. Drop a perpendicular from C to meet AB at D. Measure CD (3mks)
    4. Find the area of triangle ABC. (2mks)
19. A motorist left Embu for Nairobi a distance of 240km at 8:00 a.m. and travelled at average speed of 90km/hr. Another motorist left Nairobi for Embu at 8:30a.m and travelled at 100km/hr. Find;
    1. The time they met. (3mks)
    2. How far they met from Nairobi. (3mks)
    3. The time of the day each motorist arrived at his destination. (4mks)
20. On the graph paper provided, plot the triangle whose coordinates are P(1,3), Q(2,1), R(3,4) (1mk)
    1. On the same grid draw
       1. P’Q’R’ the image of PQR under an enlargement centre (0, 0) scale factor -1 and state its co-ordinates. (3mks)
       2. P”Q”R” the image of P’Q’R’ under rotation +90o about the origin and state the coordinates of P”Q”R”. (3mks)
       3. P”’Q’”R”’ the image of P”Q”R” under reflection y=x and state its co-ordinates. (3mks)
          

MARKING SCHEME:

1. Solve the following simultaneous equation (3mks)
   2x + 3y = 8
   5x – y = 3
   • Ans
     1 (2x + 3y = 8)
     3 (5x – y = 3)
     
         2x + 3y = 8
     + 15x – 3y = 9
          17x = 17
     x = 1
     
     5x – y = 3
     5 – 3 = y
     y = 2
2. The internal and external diameters of a spherical shell are 12cm and 8cm respectively. Calculate the volume of material of the shell. (3mks)
   • V =4/3×22/7×6³=905.14cm³
     V =4/3×22/7×4³=268.19cm³
     Shell                 636.953cm³
     = 636.953cm³
3. Use reciprocal tables and square root tables to evaluate: (3mks)
   •      1    +√2.458
      3.953
     Ans:
   • 0.2529+1.568
     = 1.821
4. Evaluate without using a calculator (3mks)
   (-9+(-7)×(-8)-(-5)
      (-2+(-6)÷3×6)
5. Solve √1.843×0.048 using logarithm tables. (3mks)
                    11.53
   

   number	std.form	log
   1.843	1.843 × 10º	0.2655
   0.048	4.8 × 10-2	2.6812
   		2.9467
   11.53	1.153 × 101	1.0619
   		3.8848

   3 + 0.8849
   3        3
   1.972 × 10^-1
   = 0.1972
6.                     
   1. Find the gradient of the straight line passing through the points P (2,3) and Q (8,-6) (1mk)
      • Gradient = (3--6)
                          (2-8)
        =  9 
          (-6)
        = (-3)
             2
   2. hence find the equation of a line parallel to the straight line and passing through R (1,2) in the form of y=mx+c. (3mks)
      • Ans
        (x, y) (1,2) (-3)/2
        (y-2)/(x-1)=(-3)/2
        y – 2 = (-3)/2 x+3/2
        y = (-3)/2 x+7/2
7. The corresponding sides of two similar regular pentagons are 3cm and 7cm respectively. (3mks)
   1. Find the ratio of their areas.
      • LSF =  3 
                   7
        ASF =  9  
                   49
   2. Calculate the area of the larger if the area of the smaller is 36cm².
      •            4
        49 ×36=196
         9
         1
        = 196cm².
8. A triangular flower garden measure 10m, 15m and 24m. Find the area of the garden. (3mks)
   
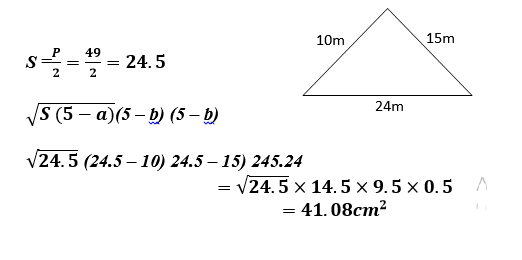
9. Two arms of a pair of divider are spread so that the angle between them is 90º. Find the area of the sector formed if the length of an arm is 8.2cm. (3mks)
   
10. Without using a calculator, evaluate; (3mks)
    (2 1⁄5+2⁄3 of3 3⁄4-4 1⁄6)
    (1 1⁄4-2 2⁄5 ÷1 1⁄3-3 3⁄4)
    • 11/5+2/3×15/4-25/6
      11/5+5/2-25/6
      = 8/15
      5/4-(12/5÷4/3)-15/4
      5/4-9/5-15/4
      8/15×10/43
      = -16  
         129
11. An observer stationed 20m away from a tall building finds that the angle of elevation of the top of the building is 68º and angle of its foot is 50º. Calculate the height of the building. (3mks)
    
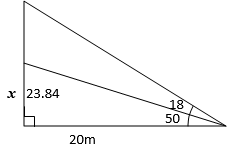
    tan 50 = x 
                  20
    x = 23.84
    tan 60 = h
                 20
    h = 34.64
    h = 10.8
12. Factorize the following; (2mks)
    • 4x² + 7x + 3
      S=7 P=12
      (4x²+4x)+(3x+3)
      4x(x+1)+3(x+1)
      (4x+3)(x+1)
13. Find the integral values of the inequalities. (3mks)
    -1 ≤ 3x -1 < 5
    • 3x – 1 < 5
      3x < 6
      x < 2
      -1 ≤ 3x – 1
      0 ≤ 3x
      0 ≤ x
      0 ≤ x < 2
      0,1 integral values.
14. Three years ago, Juma was three times as old. as Ali and in two years time, the sum of their ages will be 62. Determine their present ages (3mks)
    •                   3 years ago             present              2 yrs
      Juma              x – 3                     x (42)                x+2
      Sli                   y – 3                     y (16)                y+2
                   x – 3 = 3(y – 3)             x + 2 + y + 2 = 62        x + y = 58
                   x 3 = 3y – 9                  x + y = 58                     x = 58 - 16
                   x – 3y = =6                – x – 3y = -6
                                                      4y = 64
                                                       y = 16
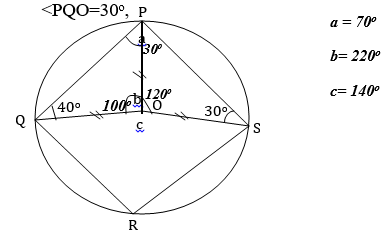
15. The figure below shows a cirlcle with centre O. Find the values of a, b, c and if <PQO=30º,
    
16. A tourist visited Kenya with 2500 US dollars and changed the US dollars into Kenya shillings at a local bank in Kenya when the exchange rates at the time were as follows:
                                          Buying           Selling
    1 US dollar                   shs.78.45      shs. 78.55
    1 Sterling Pound          shs.120.25    shs. 120.45
    
    1. How much did he get in Kenya shillings? (2mks)
       • 2500 X 78.45
         = 196125 /=
    2. While in Kenya he used shs. 80,000 and after his stay he converted the remaining amount into Sterling pounds. Calculate to 2 decimal places the Sterling pounds that he got (2mks)
       • 196125
         80000  
         116125
         116125
         120.45
         = 964.09 Sterling Pounds.
17. The table below shows the names of 200 persons measured to the nearest kg
    

    Mass (kg)	40-49	50-59	60-69	70-79	80-89	90-99	100-109
    No. of persons	9	27	70	50	26	12	6

    1. State the modal class (1mk)
       • 60 - 69
    2. Calculate the mean mass (5mks)
       

       Class	x	F	Fx	C.F
       40-49 50-59 60-69 70-79 80-89 90-99 100-109	44.5 54.5 64.5 74.5 84.5 94.5 104.5	9 27 70 50 26 12 6      . 200	400.5 1471.5 4515 3725 2197 1134 627   . 14070	9 36 106 156 182 194 200

       x ̅=14070
              200
       =70.35
    3. Calculate the median mass (4mks)
       59.5+(200/2-36)×10)
                          70
       =68.64
18. Using a ruler and pair of compasses only.
    1. Construct a triangle ABC in which AB=9cm, AC=6cm and BAC=37 ½º. (5mks)
    2. Drop a perpendicular from C to meet AB at D. Measure CD and hence find the area of triangle ABC.
19. A motorist left Embu for Nairobi a distance of 240km at 8:00 a.m and travelled at average speed of 90km/hr. Another motorist left Nairobi for Embu at 8:30a.m and travelled at 100km/hr. Find;
    1. The time they met. (3mks)
       
       8: 00 am → 90km/h
       T= 30mins
       S= 90km/h
       D= 45km
       D.A = 195km
       RS = 190km/hr
       T = 39
             38
       8.30 am
          62 
       9.32 am
    2. How far they met from Nairobi. (3mks)
       T= 39/38hr
       S = 100km/hr
       D= 102.63 km
    3. The time of the day each motorist arrived at his destination. (4mks)
       Embu → Nairobi     NairobiEmbu
       D = 240km              D = 240km
       S = 90km/hr            S = 100km/hr
       T= 2hr 40mins        T = 2h 24mins
       8.00                        8.30
       2.40                        2.24
       10.40am                10.54 am
20.                
    1. 88 km ± 1 and 049º ± 1
    2. 96km ± and 254º  ± 1
    3. 90 + 31
       = 121 ± 2º