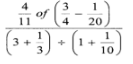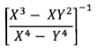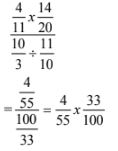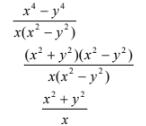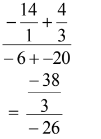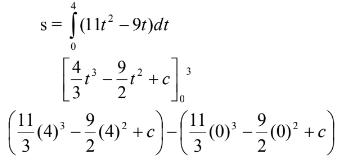Mathematics Paper 1 Questions And Answers - Form 4 Term 2 Opener 2021

INSTRUCTION

This paper consist of TWO sections: section I and Section II.
Answer ALL the questions in Section I and only five questions from section II.
Show all the steps in your calculations, giving your answers at each stage in the stage in the spaces below each question.
Marks may be given for correct working even if the answer is wrong.
Non-programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise.

Evaluate without using a calculator or Mathematical tables leaving your answer in the simplest form. (3mks)
A Kenya bank buys and sells foreign currencies as shown.
Buying (Ksh) Selling (Ksh)
1 Euro 84.15 84.26
100 Japanese Yen 65.37 65.45
A Japanese travelling from France to Kenya had 5000 Euros. He converted all the 5000 Euros to Kenya shilling at the bank. While in Kenya, he spent a total of Ksh.289850 and then converted the remaining Kenya shilling to Japanese Yens at the bank. Calculate the amount in Japanese Yen that he received. (3mks)
Line L1 passes through the points A (1, −2) and B (3, −4). Find the equation of line L2 passing through the mid-point of AB and perpendicular to L1, leaving your answer in the form ax+by+c=0. (4mks)
The curved surface area of a cylindrical container is 1980cm². If the radius of the container is 21cm, calculate to one decimal place the capacity of the container in litres (3 mks) Take π = ²²/₇
State all the integral values of a which satisfy the inequality. (4mks)
3a + 2 ≤ 2a + 3 ≤ 4a + 15
4 5 6
1. Using a pair of compasses and a ruler only construct a triangle ABC such that AB= 4cm, BC = 6cm and ZABC = 135°. (2mks)
2. Construct the height of triangle ABC in (a) above taking AB as the base, hence calculate the area of triangle ABC. (2 mks)
One interior angle of a polygon is equal to 800 and each of the other interior angles are 128°. Find the number of sides of the polygon. (3 mks)
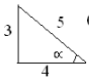
Given that tan c = 0.75, without using tables or a calculator find cos (180— ct) (3mks)
Simplify: (3 marks)
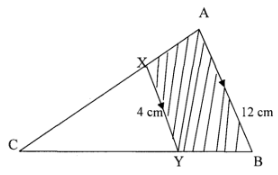
In the figure below, lines AB and XY are parallel.

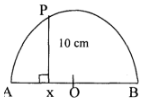
If the area of the shaded region is 36 cm², find the area of triangle CXY. (3 marks)
In the figure below 0 is the centre of the circle diameter AB. <AXP = 900, AX 4cm and PX 10 cm. Calculate the radius of the semi-circle. (3 mks)
All prime numbers between ten and twenty are arranged in descending order to form a number.
1. Write down the number. (1 mk)
2. State the total value of the third digit of the number formed in (i) above. (1 mk)
Find the value of x in the following equations: (3mks)
(4)^−2x = (¹/₃₂)^3x−4
The marked price of a car in a dealer’s shop was Kshs 450,000. Wekesa bought the car at 7% discount. The dealer still made a profit of 13%. Calculate the amount of money the dealer had paid for the car. (3 mks)
Use tables of cubes, square roots and reciprocals to evaluate. (3mks)
3
(0.3375)³ − √337.5
Without using tables or a calculator, evaluate (3mks)
(−2) × 7 + (−4) ÷ (−3)
3 × −2 + 5 × (−4)
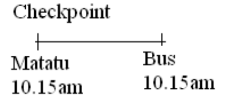
1. A bus traveling at 99km/hr passes a checkpoint at l0.00am and a matatu Traveling at 32km/hr in the same direction passes through the check point at 10.l5am. If the bus and the matatu continue at their uniform speeds, find the time the matatu will overtake the bus. (6 mks)
2. Two passenger trains A and B which are 240m apart and travelling in opposite directions at 164km/h and 88km/h respectively approach one another on a straight railway line. Train A is 150 metres long and train B is 100m long. Determine the time in seconds that elapses before the two trains completely pass each other. (4 mks)
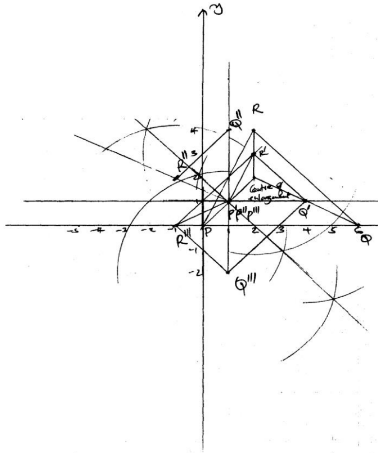
The vertices of triangle PQR are P(O,O), Q(6, 0) and R(2, 4)
1. Draw triangle PQR on the grid provided. (lmk)
2. Triangle P1Q1R’ is the image of a triangle PQR under an enlargement scale factor , ½ and centre (2, 2). Write down the coordinates of triangle P¹Q¹R¹and plot on the same grid. (2 mks)
3. Draw triangle P¹¹Q¹¹R¹¹ the image of triangle P¹Q¹R¹under a positive quarter turn about points (1, 1). (3 mks)
4. Draw a triangle P¹¹¹Q¹¹¹R¹¹¹ the image of triangle P¹¹Q¹¹R¹¹ under reflection in the line y=1. (2mks)
5. Describe fully a single transformation that maps triangle P¹¹¹Q¹¹¹R¹¹¹ onto triangle P¹Q¹R¹(2 mks)
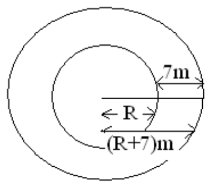
A circular lawn is surrounded by a path of uniform width of 7m. The area of the path is 21% that of the lawn.
1. Calculate the radius of the lawn. (4 mks)
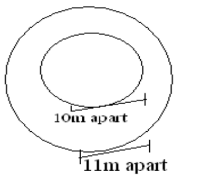
2. Given further that the path surrounding the lawn is fenced on both sides by barbed wire on posts at intervals of 10 metres and 11 metres on the inner and outer sides respectively. Calculate the total number of posts required for the fence. (4 mks)
3. Calculate the total cost of the posts if one post costs sh 105. (2 mks) Page 10 of 15
The velocity of a particle t seconds after passing a fixed point 0, is given by V = at² + bt m/s, where a and b are constants. Given that its velocity is 2 m/s when t =1 sec and it returns to 0 when t = 4.5 secs, calculate;
1. The values of a and b. (4 mks)
2. Hence find;
  1. The values oft when the particle is instantaneously at rest. (2 mks)
  2. The total distance travelled by the particle during the first 4 seconds. (2 mks)
  3. The maximum velocity attained by the particle. (2mks)

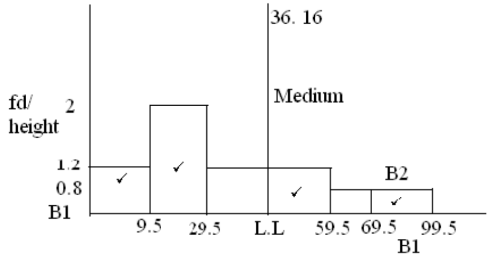
The table below shows marks obtained by 120 candidates. Frequencies for all the groups and also the area and height of the rectangle for the group 30 — 60 marks are shown.

marks	0-10	10-30	30-60	60-70	70-100
Frequency	12	40	36	8	24
Area of rectangle			36
Height of rectangle			1.2

1. Complete the table. (2mks)
2. On the grid provided below, draw he histogram to represent the distribution. (4mks)
3. State the group in which the median mark lies. (1 mk)
4. A vertical line drawn through the median mark divides the total area of the histogram into two equal parts. Using this information, estimate the median mark. (2 mks)

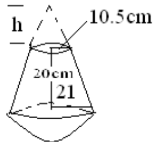
A frustum of a cone is such that one of its ends is hemispherical with a radius of2lcm and the other top end is circular with a radius of 10.5cm .The perpendicular distance between the centres of the circular parts is 20cm. Find;
1. The slant length of the original cone. (3 mks)
2. The slant length of the frustum. (2mks)
3. The surface area of the frustum. (5 mks)
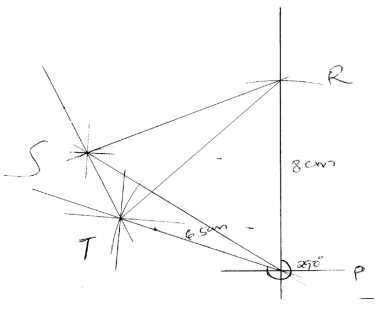
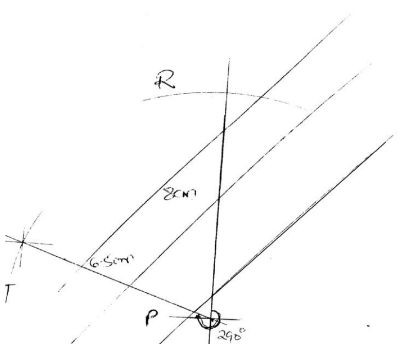
Four towns P, R, T and S are such that R is 80km directly to the north of P and T is on a bearing of 290° from P at a distance of 65km. S is on a bearing of 330° from T and a distance of 30 km. Using a scale of 1cm to represent 10km, make an accurate scale drawing to show the relative position of the towns. (4mks)
Find:
1. The distance and the bearing of R from T (3mks)
2. The distance and the bearing of S from R (2mks)
3. The bearing of P from S (lmk)
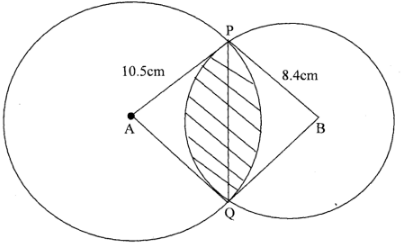
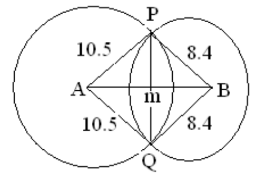
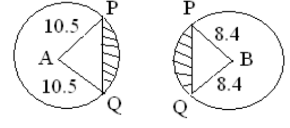
The figure below shows two circles of radii 10.5 and 8.4cm and with centres A and B respectively. The common chord PQ 9cm.
1. Calculate angle PAQ. (2 mks)
2. Calculate angle PBQ. (2 mks)
3. Calculate the area of the shaded part. (6 mks)

MARKING SCHEME

=³/₁₂₅
500 x 84.15 – 289850
= 130,900
But 100 yens ≡ 65 – 45
? 130900
= 200000 yens
Gradient L1 = −4 + 2 = −2 = −1
3−1 2
→Gradient L2 = 1
Mid- point AB = (2, −3)
∴ y + 3 =1
x −2
→y + 3 = x − 2
∴ −x+y+5=0
Πdh = 1980
²²/₇ × 42 × h
h=15cm
Vol = ²²/₇ × 21 × 21 × 15
= 20790cm3
= 20.79li
3a + 2 ≤ 2a + 3
4 5
→ 5(3a+2) ≤ 4(2a+3)
15a + 10≤8a + 12
7a ≤2
a≤²/₇
2a + 3 ≤ 4a + 15
5 6
6(2a+3) ≤ 5(4a +15)
12a +18 ≤ 20a +75
−8a ≤ 57
A ≤ −⁵⁷/₈ → −⁵⁷/₈ ≤ a ≤ ²/₇
Intergal values
−7, −6, −5, −4, −3, −2, −1, & 0
80 + (n –1)128 = 180n – 360 or its equivalent
→ 80 + 128n – 128 = 180n – 360
–52n =–312
n = 6
→ Cos ∝ =⁴/₅
Cos (180 - ∝) = ⁴/₅
Let Area c x y = x
L.S. F = ⁴/₁₂ = ¹/₃
A.S.F = ¹/₉
→ 1 = x
9 x+36
→9x =x +36
8x = 36
x=4.5cm²
XO = (r–4)cm
OP = rcm
XP = 10cm
→ r² = 100 + (r–4)²
r² = 100 + r²–8r +16
→ 8r = 116
r = 14.5cm
1. 19, 171, 311
2. 300
(¼)^2x = (¹/₃₂)^3x–4
(½)^4x = (½)^15x–20
→4x = 15x – 20
– 11x = –20
X =²⁰/₁₁
450000 = 100%
? = 93%
Cash price = 418500 shillings
But 418500 = 113%
? = 100%
= 370353.9823 shillings
(3.375 x ¹/₁₀)³ = 0.038441
(3.375 x 100)^½ = 18.372
= 3
–18.333559
(−3) x 1 = (−3) x 1 × 10
18.33 1.833
= (–3) x (0.5455) x ¹/₁₀
= –0.16365
=–38 × 1
3 –26
=38 × 1 = 19
3 26 39
1. Distance between matatu and bus = distance covered by bus for 15min
  = 99km/h x ¹⁵/₆₀ = 24.75km
  Time taken for matatu to catch up with bus
  = Distance between
  Relative speed
  = 24.75km = 0.75hrs = 45min
  33km/h
  → Overtaking will take place at
  10.15am + 45min = 11.00am
2. Time taken = Distance
  R.S
  =(150 + 240 +100)
  252km / h
  But 252km/h = 70m/s
  T = 490m =7secs
  70m/s
2. P’ (1, 1) Q’(4, 1) R’ (2, 3)
3. P”(1, 1) Q”(1, 4) R” (−1, 2)
4. P’” (1, 1) Q’”(1, −2) R’” (−1, 0)
5. Reflection through the mirror line y = −x+2
  Gradient = −1
  → y−1 = −1
  x −1
  y – 1 = −x +1
1. let radius lawn Rm
  radius of lawn r path = (R+7)m
  Area of the lawn = πR²m²
  Area of the lawn + path = π(R +7)²
  = π(R² + 14R + 49)
  = (R² + 14R + 49) πm²
  Area of the path = (R² + 14R +49) πR²
  = πR² + 14πR + 49π – πR²
  = 14πR + 49π = (14R + 49)π
  Area of the path also equal to 21% of area of lawn → 21% of πR²
  = 0.21πR²
  → 0.21πR² = (14R +49)π
  0.21R² = 14 R + 49
  0.21R²– 14R – 49 =0
  21R²- 1400R – 4900-0
  3R²-200R – 700= 0
  
  = 200 ± 220 → −20 or 420
  6 6 6
  = −20 impossible
  6
  Hence R =70m
2. Perimeter of inner fence = 2πR
  = 2 3.14 x 70 = 439.88m
  No of post 43.988 = 43.988 = 44 posts
  10
  Perimeter of outer fence
  = 2x3.14 x 77 = 483.868m
  No of posts = 483.868 = 43.988
  11
  = 44 posts
  Total number of posts = 44 + 44 = 88posts
3. Total cost
  88 x 103 −1 = Sh. 9240
1. v = at² +bt m/s
  at t = 1sec
  v= 2m/s
  a + b = 2 ..........................(i)
  at rest v = 0, t = 45
  (4.5)²a + 45b = 0
  20.25 a + 4.5 b = 0 .............(ii)
  Solving (i) and (ii) simultaneously
  a = 2−b
  20.25 ( 2−b) + 4.5b = 0
  40.5 + 4.5 b = 0
  b = −40.5 = −9
  4.5
  → a = 2 –(−9) = 11
  v = 11t²−9tm/s
2. 1. at rest, v = 0
    11t²– 9t = 0
    (11t – a)t = 0
    → t=0 or 11t = 9 →t =⁹/₁₁
  2. (234.67 – 72 + c) – (c) = 162.67 m
  3. at max velocity a = 0
    a = dv
    dt
    v = 11t²– 9t
    a = 22t – a
    22t – 9 = 0
    t = ⁹/₂₂
    v = 11 (⁹/₂₂)² − 9(⁹/₂₂)
    =11⁸¹/₄₄ − ⁸¹/₂₂=⁸¹/₄₄ − ⁸¹/₂₂ = 81 − 162
    44
    =⁻⁸¹/₄₄m/s deceleration

marks	0-10	10-30	30-60	60-70	70-100
Frequency	12	40	36	8	24
Area of rectangle	12	40	36	8	24
Height of rectangle	12	2	1.2	0.8	0.8
L.L	9.5	29.5	59.5	69.5	99.5
C.F	12	52	88	96	120

Medium position = N +1 = 121 = 60.5
2 2
in the class 30- 60
½ total area = ¹²⁰/₂units² = 60units²
=12+40+8 = 60units²
But 8 = 6.66 + 29.5 = 36.16
1−2

1. h = 10.5
  20+h 21
  21h = 10.5h +210
  10.5h = 210
  h = 20cm
  → H = 40cm
  L² = 21² + 40²L² = 441 + 1600
  L = 45.17742799cm
2. L2 = 20² + 10.5²L2 400 + 110.25
  L = 22.588714cm
  → slant length of frustrum
  = 45.17742799 – 22.588714
  = 22.58871399
3. TOTAL S.A = πr² + (πRL – πrL) + 2πR2
  (²²/₇ × 10.5 × 10.5) + (²²/₇ × 21 × 45.17742799) − (²²/₇ × 10.5 × 22.588714)) + 2²²/₇ × 21 × 21
  = 346.5 + 2981.7104 – 745.427562 + 2772
  = 5354.782685cm²
1. 84km, 042°
2. 80km, 065°
3. 120°
1. < PAQ = <PAM + <QAM
  < PAM = sinθ1 = 4.5 = 0.4286
  10.5
  Sin ^-1(0.4286) = 25.38°
  < QAM = <PAM = 25.38
  →<LAP = 25.38x2= 50.76
2. <PBQ = < PBM + <QBM
  < PBM = sin∝1 = 45 = 0.5357
  84
  Sin^-1(0.5357) = 32.39°
  < PBM = <QBM = 32.39º
  <PBQ = 32.39° x 2 = 64.78
3. area of segment = area of a section – area of D
  Taking (i)
  =(^50.76/₃₆₀ × 3.14 × 10.5²) − (½ × 10.5 sin 50.76)
  = 48.84 – 42.69 = 6.15cm²
  Taking (ii)
  =(^64.78/₃₆₀ × 3.14 × 8.4²) − (½ × 8.4 × 8.4 × sin 64.78)
  = 39.89 – 31.92 = 7.97cm²
  = (6.15 + 7.97) cm² = 14.12cm²