INSTRUCTIONS TO CANDIDATES
- This paper consists of two sections: Section I and Section II.
- Answer ALL questions in section 1 and ONLY FIVE questions from section II
- All answers and workings must be written on the question paper in the spaces provided below each question.
- Show all the steps in your calculation, giving your answer at each stage in the spaces below each question.
- Non – Programmable silent electronic calculators and KNEC mathematical tables may be used, except where stated otherwise.
FOR EXAMINERS USE ONLY
SECTION I
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
TOTAL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SECTION II GRAND TOTAL
|
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
TOTAL |
|
|
|
|
|
|
|
|
|
|

QUESTIONS
SECTION I
Answer all questions in the spaces provided
- Ballast, sand and cement are mixed in the ratio 6:4:3. The cost of 6 tonnes of sand is sh. 6000, 7 tonnes of ballast cost sh. 9100 and 3 tonnes of cement cost sh. 24000. Calculate the cost of 10 tonnes of the mixture to the nearest shilling. (3mks)
- The 2nd term of an A.P is three times the 7th term. If the 9th term is 1, find the 1st term and the common difference. (3mks)
- Given that x=2-√3, simplify x2-x√3. (3mks)
- Write the expansion of
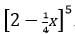 . Hence, use the expansion to find the value of (1.96)5 correct to 3 decimal places. (4mks)
. Hence, use the expansion to find the value of (1.96)5 correct to 3 decimal places. (4mks) - The figure below shows a cuboid labeled ABCDEFGH. Point x is the mid-point of BD. AB=15cm, BC=8cm and CF=5cm.
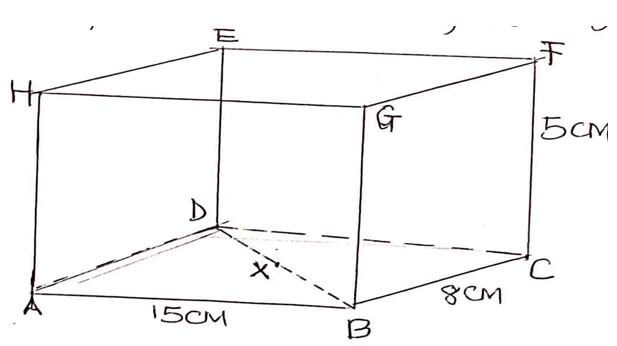
- Calculate the length XC. (2mks)
- Calculate the angle <FXC (2mks)
- The area A of a sector of a circle of radius r varies jointly as r2 and Ѳ, the angle of the sector at the centre of the circle. If A=30cm2, r=8cm, and Ѳ=24º, find A when Ѳ=48º and r=4cm. (3mks)
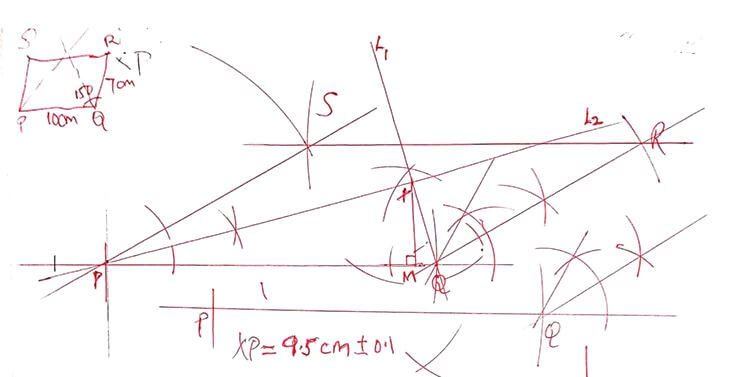
- The figure below shows a circle and a point R outside the circle.
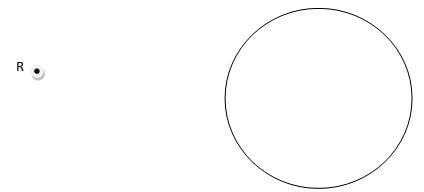
- Locate the centre of the circle. (1mk)
- Using a ruler and a pair of compasses only, construct two tangents to the circle from R. (3mks)
- Solve for y in [log10y ]2=3-log10y2 (3mks)
- Find the percentage error in calculating the area of a square of length 20cm. (3mks)
- An old laptop has a cash price of sh 18000. A trader offers a down payment of sh 5000 and 15 monthly installments of shs. 1050 each. Calculate the rate of compound interest charged per month for the laptop. (3mks)
- Find the inverse of the matrix
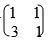 hence determine the point of intersection of the Lines
hence determine the point of intersection of the Lines
y + x = 7
3x + y = 15 (3mks) - A bag contains 3 blue marbles, 4 white marbles and 3 red ones. Two marbles are drawn from the bag, one at a time without replacement. Find the probability that one of them is red and the other is white. (3mks)
-
- Draw the line of best fit for the values of E and C given in the table below: (3mks)
E
4
7
10
13
16
19
c
15.1
20.2
23.9
27.3
30.1
33.1

- Write the equation connecting E and C. (1mk)
- Draw the line of best fit for the values of E and C given in the table below: (3mks)
- Given that cos Ѳ = 0.6 and Ѳ is an acute angle, find.
- Ѳ (1mk)
- Tan Ѳ (2mks)
- Find the position vector of a point p that divides AB in the ratio 3:5, where
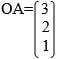 and
and 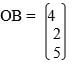 (2mks)
(2mks) - The positions of points A and B are A(25ºN, 45ºE) and B(25ºN, 63ºE) respectively. Calculate the distance between the points along the latitude. (take the radius of the earth to be 6370km) (2mks)
SECTION II
Answer any FIVE questions from this section - A metal water pipe has an internal radius of 10cm. the pipe is made of a metal of uniform thickness of 1cm.
- Find the volume, in cubic centimeters of metal used to make a portion of the pipe, 5m long. (4mks)
- Given that the metal used to make the pipe has a density of 8.5g/cm3, find the mass of the piece of pipe in kilograms. (3mks)
- Water runs through the pipe at a rate of 30cm per second. Find the time taken to fill a water tank of capacity 50000 litres. (3mks)
- The table below shows the distribution of masses of a sample of students in a certain school.
Using 47 as your assumed mean, calculate:Mass (kg)
20-24
25-29
30-34
35-39
40-44
45-49
50-54
55-59
60-64
65-69
No. of pupils
1
5
9
11
20
20
19
8
4
3
- The actual mean mass. (5mks)
- The standard deviation of the mass. (5mks)
- The length and breadth of a rectangle are given as (6x-1) and (x-2) metres respectively. If the length and breadth are each increased by 4 metres, the new area is three times that of the original rectangle.
- Form an equation in x and solve it. (4mks)
- Find the dimensions of the original rectangle. (2mks)
- Express the increase in area as a percentage of the original area. (4mks)
- The equation of a curve is given by y = 1+ 3sinx.
- Complete the table below for y=1+3sinx correct to 1 decimal place. (2mks)
xo
0
30
60
90
120
150
180
210
240
270
300
330
360
Y=1+3sinx
1
3.6
1
-0.5
-1.6
-
- On the grid provided, draw the graph of y=1+3sinx for 0≤x≤360º. (3mks)

- State the period of the curve y=1+3sinx. (1mk)
- On the grid provided, draw the graph of y=1+3sinx for 0≤x≤360º. (3mks)
- On the same grid draw the graph of y=tanx for 90º≤x≤270º. (3mks)
- Use the graphs to solve the equation 1+3sinx=tanx for 90º≤x≤270º. (3mks)
- Complete the table below for y=1+3sinx correct to 1 decimal place. (2mks)
- Mrs. Kihara is a clerk on a basic monthly salary of ksh. 16000. She also gets a house allowance of ksh. 12000. A medical allowance of ksh. 3060 and a commuter allowance of ksh. 4635. She has a life insurance policy for which she pays ksh 800 per month. She claims personal relief of shs. 1056 and insurance relief of kshs. 120 per month. Use the tax table below;
Income in K£ per month
Rate (%)
1-484
10
485-940
15
941-1396
20
1397-1852
25
Over 1852
30
- Calculate Mrs. Kihara’s taxable income in K£. (3mks)
- Using the table above, calculate her PAYE. (4mks)
- In addition to the PAYE, the following deductions are made on her pay every month NHIF ksh. 600. Co-operative share Khs. 4800. Calculate her net salary. (3mks)
- A quadrilateral with vertices at K(1,1) L(4,1) M(2,3 and N(1,3) is transformed by a matrix.
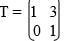 to a quadrilateral K΄L΄M΄N΄.
to a quadrilateral K΄L΄M΄N΄.- Determine the coordinates of the image. (3mks)
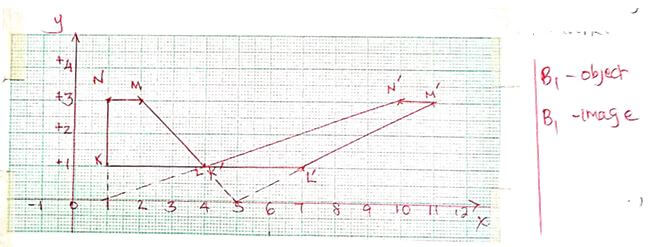
- On the grid provided draw the object and the image. (2mks)

- Describe fully the transformation which maps KLMN onto K΄L΄M΄N΄. (2mks)
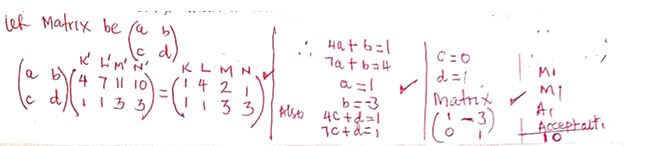
- Find a matrix which maps K΄L΄M΄N΄ onto KLMN. (3mks)
-
- Complete the table for the function y=x^3+3x+6 for the range -2≤x≤8 (2mks)
x
-2
-1
0
1
2
3
4
5
6
7
8
y
- Using trapezium rule, find the area bounded by the curve, lines x=-2 and x=8 (3mks)
- Using mid-ordinate with 5 strips, find the area bounded by the curve, lines x=-2 and x=8 (3mks)
- Find the exact area of the region described in 23 (c) above. (2mks)
- Complete the table for the function y=x^3+3x+6 for the range -2≤x≤8 (2mks)
- A body moves in a straight line such that at any time t seconds, its distance S metres from the starting point is given by S=8t-t2.
- How fast is the body moving at:
- T= 1 second (2mks)
- T=3 seconds (2mks)
- Calculate the maximum displacement from the starting point that the body achieves. (3mks)
- Calculate the acceleration of the body during the motion. (1mk)
- After how long will the body be back at the starting point? (2mks)
- How fast is the body moving at:

MARKING SCHEME
SECTION I
Answer all questions in the spaces provided
- Ballast, sand and cement are mixed in the ratio 6:4:3. The cost of 6 tonnes of sand is sh. 6000, 7 tonnes of ballast cost sh. 9100 and 3 tonnes of cement cost sh. 24000. Calculate the cost of 10 tonnes of the mixture to the nearest shilling. (3mks)
6 + 4 + 3 = 13 tonnes
cost of 6 tonnes of ballast = 6/7 x 9100
cost of 4 tonnes of sand = 4/6 x 600
= ks 4000
cost of 3 tonnes of cement = 3/3 x 24000
= ksh 24000
13 tonnes of mixture cost = 7800 + 400 + 24000
= sh 35,800
therefore cost of 10 tonnes = 10/13 x 35800
=sh 27 538.4615
= sh 27, 538 - The 2nd term of an A.P is three times the 7th term. If the 9th term is 1, find the 1st term and the common difference. (3mks)
a + d = 3(a + 6d)
therefore 2a + nd = 0(i)
let ath term be a + 8d
therefore a + 8d = 1 (ii)
2a + 17d = 0
2 x (a + 8d = 1)
2a + 17d = 0
- 2a + 16d = 2
d = -2
a + -16 = 1
a = 17 - Given that x=2-√3, simplify x2-x√3. (3mks)
x2 => (2 - √3)2
= 7 - 4√3
x√3 => (2 - √3) √3
= 2√3 + 3
=> 7 - 4√3 - (2√3 - 3)
7 - 4√3 - 2√ + 3
10 - 6√3 - Write the expansion of
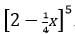 . Hence, use the expansion to find the value of (1.96)5 correct to 3 decimal places. (4mks)
. Hence, use the expansion to find the value of (1.96)5 correct to 3 decimal places. (4mks)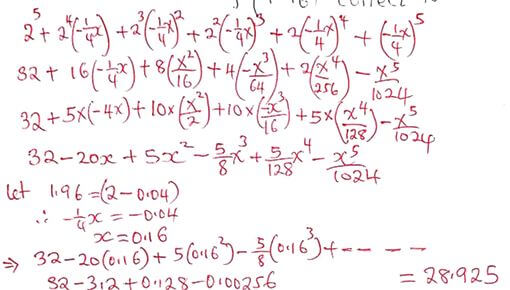
- The figure below shows a cuboid labeled ABCDEFGH. Point x is the mid-point of BD. AB=15cm, BC=8cm and CF=5cm.
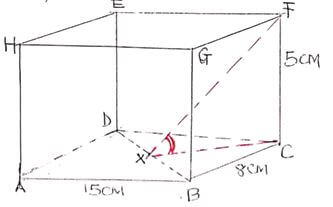
- Calculate the length XC. (2mks)
Diagonal AC = √152 + 82
= √289
= 17
therefore XC = 1/2 x 17
= 8.5 - Calculate the angle <FXC (2mks)
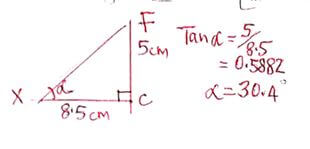
- Calculate the length XC. (2mks)
- The area A of a sector of a circle of radius r varies jointly as r2 and Ѳ, the angle of the sector at the centre of the circle. If A=30cm2, r=8cm, and Ѳ=24º, find A when Ѳ=48º and r=4cm. (3mks)
A α r2θ
therefore A = kr2θ
30 = k x 64 x 24
therefore k = 30/1536
= 5/256
=> A = 5/256 r2θ
A = 5/256 x 16 x 48
= 15 cm2 - The figure below shows a circle and a point R outside the circle.

- Locate the centre of the circle. (1mk)
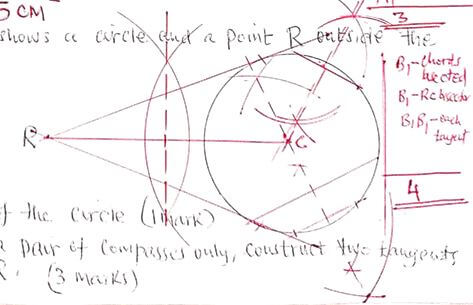
- Using a ruler and a pair of compasses only, construct two tangents to the circle from R. (3mks)
- Locate the centre of the circle. (1mk)
- Solve for y in [log10y ]2=3-log10y2 (3mks)
let log10y = u
u2 = 3 - 2u
u2 + 2u - 3 = 0
(u - 1)(u + 3) = 0
therefore u = 1 or u = -3
log 10 y = 1 or log 10 y = -3
y = 10 y = 10-3 or 1/1000 - Find the percentage error in calculating the area of a square of length 20cm. (3mks)
- An old laptop has a cash price of sh 18000. A trader offers a down payment of sh 5000 and 15 monthly installments of shs. 1050 each. Calculate the rate of compound interest charged per month for the laptop. (3mks)
total instalments = 15 x x1050
= sh 15750
borrowed amount = 18000 - 5000 = sh 13 000
A = P(1 + r/100)n
15750 = 13000(1 + r/100)15
1.21 = (1 + r/100)15
log 1.21 = 15 log (1 + r/100)
log 1.21/15 = log (1 + r/100)
= 0.005519 = log (1 + 0.01r)
1.013 = 1 + 0.01r
therefore 0.01r = 0.013
r = 1.3% - Find the inverse of the matrix
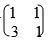 hence determine the point of intersection of the Lines
hence determine the point of intersection of the Lines
y + x = 7
3x + y = 15 (3mks)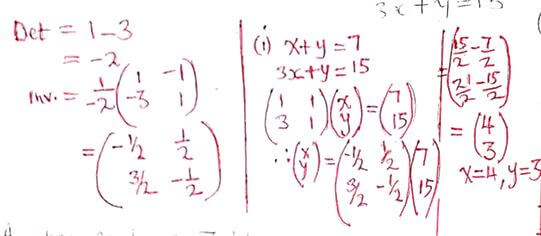
- A bag contains 3 blue marbles, 4 white marbles and 3 red ones. Two marbles are drawn from the bag, one at a time without replacement. Find the probability that one of them is red and the other is white. (3mks)
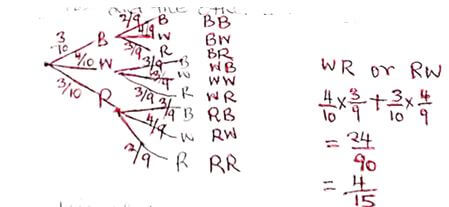
-
- Draw the line of best fit for the values of E and C given in the table below: (3mks)
E
4
7
10
13
16
19
c
15.1
20.2
23.9
27.3
30.1
33.1

- Write the equation connecting E and C. (1mk)
C = ME + K
therefore K = 10
M = gradient
using (0,10) and (4, 15.1)
gradient = 15.1 - 10
4 - 0
= 5.1 = 1.275
4
c = 51E + 10
40
or
C = 1.275E + 10
- Draw the line of best fit for the values of E and C given in the table below: (3mks)
- Given that cos Ѳ = 0.6 and Ѳ is an acute angle, find.
- Ѳ (1mk)
Ѳ = 53.21º - Tan Ѳ (2mks)
cos Ѳ = 6/10
tan Ѳ = 8/6
= 1.333
- Ѳ (1mk)
- Find the position vector of a point p that divides AB in the ratio 3:5, where
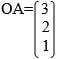 and
and 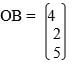 (2mks)
(2mks)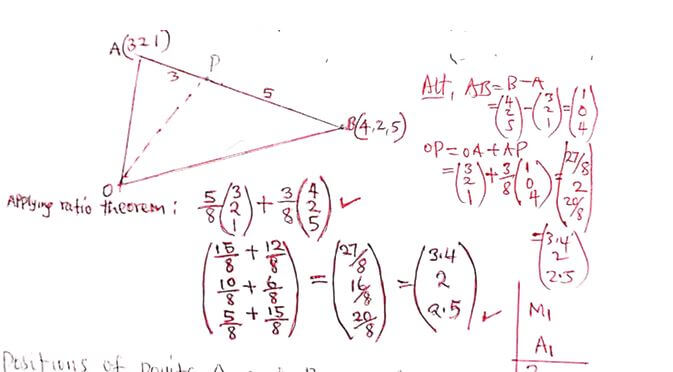
- The positions of points A and B are A(25ºN, 45ºE) and B(25ºN, 63ºE) respectively. Calculate the distance between the points along the latitude. (take the radius of the earth to be 6370km) (2mks)
let α = 63 - 45
= 18º
AB = 60 x 18 cos 25
= 978.8 nm
alternative in km
AB = 18/360 x 2π x 6370 cos 25
= 652925.73 km
360
= 1813.68 km
SECTION II
Answer any FIVE questions from this section - A metal water pipe has an internal radius of 10cm. the pipe is made of a metal of uniform thickness of 1cm.
- Find the volume, in cubic centimeters of metal used to make a portion of the pipe, 5m long. (4mks)
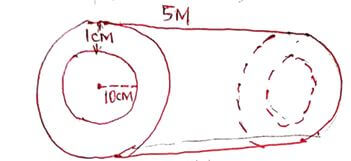
extra volume - int volume
112πx500 - 102πx500
500π(121 - 100)
= 32986.72 cm3 - Given that the metal used to make the pipe has a density of 8.5g/cm3, find the mass of the piece of pipe in kilograms. (3mks)
m = D x v
= 8.5 g/cm3 x 32986.72 cm3
= 280387.12 gms ÷ 1000
= 280.4 kg - Water runs through the pipe at a rate of 30cm per second. Find the time taken to fill a water tank of capacity 50000 litres. (3mks)
volume in 1 sec = πr2 x 30
= 102π x 30
= 9424.78 cm3
1 sec --> 9424.78cm3
? --> 50000 x 1000 cm3
= 5305.16 sec
= 5305.16 = 1.474 hrs
3600
- Find the volume, in cubic centimeters of metal used to make a portion of the pipe, 5m long. (4mks)
- The table below shows the distribution of masses of a sample of students in a certain school.
Using 47 as your assumed mean, calculate:Mass (kg)
20-24
25-29
30-34
35-39
40-44
45-49
50-54
55-59
60-64
65-69
No. of pupils
1
5
9
11
20
20
19
8
4
3
- The actual mean mass. (5mks)
mean (x) = 0 + Σfdclass x f d = x fd 20-24 22 1 -25 -25 25-29 27 5 -20 -100 30-34 32 9 -15 -135 35-39 37 11 -10 -110 40-44 42 20 -5 -100 45-49 47 20 0 0 50-54 52 19 5 95 55-59 57 8 10 80 60-64 62 4 15 60 65-69 67 3 20 60 Σf = 100 Σfd = 175
Σf
= 47 + (-175/100)
= 45.25 kg - The standard deviation of the mass. (5mks)

- The actual mean mass. (5mks)
- The length and breadth of a rectangle are given as (6x-1) and (x-2) metres respectively. If the length and breadth are each increased by 4 metres, the new area is three times that of the original rectangle.
- Form an equation in x and solve it. (4mks)

therefore (6x + 3)(x + 2) = 3(6x - 1)(x - 2)
6x2 + 120x + 3x + 6 = 3(6x2 - 12x - x + 12)
6x2 + 15x + 6 = 3(6x2 - 13x + 2)
6x2 + 15x + 6 = 15x2 - 39x + 6
12x2 - 54x = 0
6x(2x - 9) = 0
x = 0 or x = 4.5 cm - Find the dimensions of the original rectangle. (2mks)
original 6 x 4.5 - 1
= 26
4.5 - 2
= 2.5
length 26cm
width 2.5 cm - Express the increase in area as a percentage of the original area. (4mks)
original area = 26 x 2.5
= 65 cm2
new area = 65 x 3
= 195 cm2
increase = 195 - 65
= 130
130 x 100
65
= 200%
- Form an equation in x and solve it. (4mks)
- The equation of a curve is given by y = 1+ 3sinx.
- Complete the table below for y=1+3sinx correct to 1 decimal place. (2mks)
xo
0
30
60
90
120
150
180
210
240
270
300
330
360
Y=1+3sinx
1
2.5 3.6
4 3.6 2.5 1
-0.5
-1.6 -2 -1.6
0.5 1 -
- On the grid provided, draw the graph of y=1+3sinx for 0≤x≤360º. (3mks)
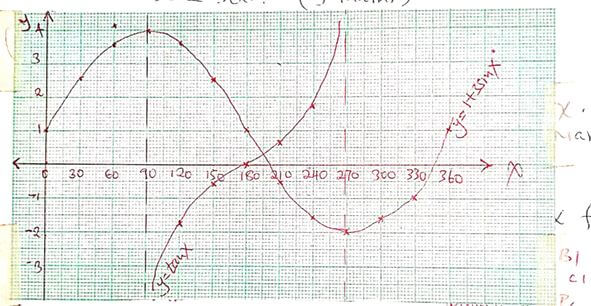
- State the period of the curve y=1+3sinx. (1mk)
- On the grid provided, draw the graph of y=1+3sinx for 0≤x≤360º. (3mks)
- On the same grid draw the graph of y=tanx for 90º≤x≤270º. (3mks)
- Use the graphs to solve the equation 1+3sinx=tanx for 90º≤x≤270º. (3mks)
intersection point at a = 195º ± 1º
- Complete the table below for y=1+3sinx correct to 1 decimal place. (2mks)
- Mrs. Kihara is a clerk on a basic monthly salary of ksh. 16000. She also gets a house allowance of ksh. 12000. A medical allowance of ksh. 3060 and a commuter allowance of ksh. 4635. She has a life insurance policy for which she pays ksh 800 per month. She claims personal relief of shs. 1056 and insurance relief of kshs. 120 per month. Use the tax table below;
Income in K£ per month
Rate (%)
1-484
10
485-940
15
941-1396
20
1397-1852
25
Over 1852
30
- Calculate Mrs. Kihara’s taxable income in K£. (3mks)
ksh (16000 + 12000 + 3060 + 4635)
= 35695
33695 = kf 1784.75
20 - Using the table above, calculate her PAYE. (4mks)
1st 484 ==> 484 x 10/100 = 48.40
2nd 456 ==> 456 x 15/100 = 68.40
3rd 456 ==> 20/100 x 456 ==> 91.20
last 388 ==> 388 x 25/100 = 97.00
total tax due = 305
305 x 20 = sh 6100
paye = total tax - reliefs
= 6100 - (1056 + 120)
= sh 4924 - In addition to the PAYE, the following deductions are made on her pay every month NHIF ksh. 600. Co-operative share Khs. 4800. Calculate her net salary. (3mks)
sh 35695 - (4924 + 600 + 4800) = sh 25371
- Calculate Mrs. Kihara’s taxable income in K£. (3mks)
- A quadrilateral with vertices at K(1,1) L(4,1) M(2,3 and N(1,3) is transformed by a matrix.
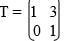 to a quadrilateral K΄L΄M΄N΄.
to a quadrilateral K΄L΄M΄N΄.- Determine the coordinates of the image. (3mks)
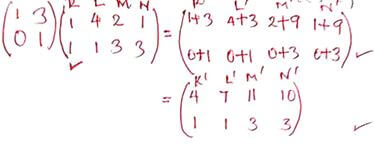
- On the grid provided draw the object and the image. (2mks)
- Describe fully the transformation which maps KLMN onto K΄L΄M΄N΄. (2mks)
shear x-axis invariant and (2, 3) ---> m1(11, 3) b1 - invariant
line must be stated
shear factor 9/3 = 3 - Find a matrix which maps K΄L΄M΄N΄ onto KLMN. (3mks)
- Determine the coordinates of the image. (3mks)
-
- Complete the table for the function y=x^3+3x+6 for the range -2≤x≤8 (2mks)
x
-2
-1
0
1
2
3
4
5
6
7
8
y
- Using trapezium rule, find the area bounded by the curve, lines x=-2 and x=8 (3mks)
xm = 2.5 cm ± 0.1 - Using mid-ordinate with 5 strips, find the area bounded by the curve, lines x=-2 and x=8 (3mks)
A = 1/2 x 10 x 2.5
= 12.5 cm2 - Find the exact area of the region described in 23 (c) above. (2mks)
- Complete the table for the function y=x^3+3x+6 for the range -2≤x≤8 (2mks)
- A body moves in a straight line such that at any time t seconds, its distance S metres from the starting point is given by S=8t-t2.
- How fast is the body moving at:
- T= 1 second (2mks)
8 - 2 x 1 = 6 m/s - T=3 seconds (2mks)
8 - 3 x 2 = 2 m/s
- T= 1 second (2mks)
- Calculate the maximum displacement from the starting point that the body achieves. (3mks)
ds/dt = 0
8 - 2t = 0
therefore t = 45
but s = 8t - t2
s = 8 x 4 - 42
= 32 - 16
= 16m - Calculate the acceleration of the body during the motion. (1mk)
v = 8 - 2t
dv/dt = -2
= -2 ms -2 ie deceleration - After how long will the body be back at the starting point? (2mks)
displacement = 0
8t - t2 = 0
t(8 - t) = 0
therefore t = 0
or
t = 8
8 seconds
- How fast is the body moving at:
Download Mathematics Paper 2 Questions and Answers - Form 4 Term 2 Opener Exams 2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

