Mathematics Questions and Answers - Form 4 Mid Term 2 2022

QUESTIONS

1. Use logarithms to 4 decimal places to evaluate: (4 marks)
   (0.7841 x √0.1356)^1/₃
          Log 84.92
2. A globe representing the earth has a radius of 0.5m. point A(0º, 10ºW), B (0º, 35ºE), P(60ºN, 110ºE) and Q(60ºN, 120ºW) are marked on the globe.
   Find the length of arc AB, leaving your answer in term of (3mks)
3. A circle centre is the point C(2,3) passes through a point P(a,b). A point M(-2 , ^-5/₂) is the mid-point of the line CP.
   
   1. Calculate the coordinates of P. (1mk)
   2. Determine the equation of the circle in the form x² +y² +ax + by + c = 0 (3mks)
4. Make a the subject of the formula:
   x = y +√(x²+ a²) (3marks)
5. Given that Sin (²/₃ x+ 20º ) - Cos (⁵/₆x + 10º) = 0. Without using a mathematical table or a calculator, determine tan (x+ 20º). (3 marks)
6. Two fair dice one a regular tetrahedron (4 faces) and the other a cube are thrown. The scores are added together. Complete the table below to show all possible outcomes. (2 mark)
   Find the probability that:
   1. The sum is 6. (1 mark)
   2. The sum is 6 or 9. (2 marks)
7. A particle moves along a straight line such that its displacement s metres from a given point is s = t³ – 5t² + 3t + 4 where t is time in seconds. Find:
   
   1. The displacement of the particle at t = 8. ( 2 marks )
   2. The velocity of the particle when t = 10. (3 marks )
8. A classroom measures (x + 2) m by (x – 5)m. If the area of the classroom is 60m².
   Find its length. (3 marks )

SECTION B

9. Lengths of 100 mango leaves from a certain mango tree were measured t the nearest centimeter and recorded as per the table below,
   Length in cm       No. of leaves
   10 to 12                     3
   13 to 15                    16
   16 to 18                    36
   19 to 21                    31
   22 to 24                    14
   
   1. On the grid provided draw a cumulative frequency graph to represent this data. (5mks)
   2. Use your graph to estimate
      
      1. The median length of the leaves (2mks)
      2. The number of leaves whose lengths lie between 13cm and 17cm. (3mks)
10.      
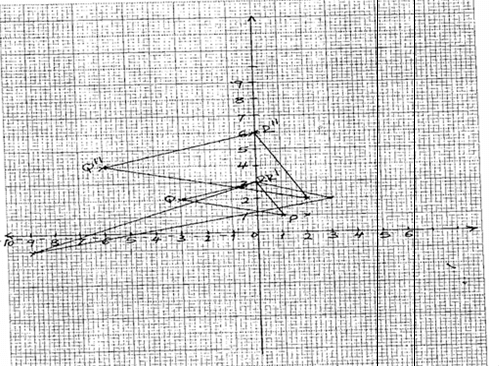
    1. Draw ΔPQR whose vertices are P (1, 1), Q (-3, 2) and R (0, 3) on the grid provided.(1mk)
       Find and draw the image of ΔPQR under the transformation whose matrix (³₁ ⁰₁) is and label the image P¹Q¹R¹. (2 marks)
    2. P¹Q¹R¹ is then transformed into P¹¹Q¹¹R¹¹ by the transformation with the matrix (^-1₁ ⁰₃) .Find the co-ordinates of P¹¹Q¹¹R¹¹ and draw P¹¹Q¹¹R¹¹. (3 marks)
    3. Describe fully the single transformation which maps PQR onto P¹¹Q¹¹R¹¹ find the matrix of this transformation. (3 marks)
    4. Describe fully the single transformation which maps PQR onto P¹¹Q¹¹R¹¹ find the matrix of this transformation. (3 marks)

MARKING SCHEME

1. 
   

   No	Log
   0.7841 0.1356½ Log 84.92 = 1.929 0.5310	1.8944 1.1323 = 1.5662    2          14606 1.2853 1.1753 3/3 + 2.1753 = 1.7251             3 1.7251

2. Difference in longitude = 10 + 35 = 45º
   length of arc AB = ⁴⁵/₃₆₀ x 2 x π x 0.5
   = ¹/₈π = 0.125π
3.    
   1. 2 + a = 2 = 2 + a = -4
        2
      a  = -6
      3 + b = -2.5 = 3 + b = -5
         2
      b = -8
   2. (a, b) = (-6,8)
      r = √(2 --6)² + (3--8)² = √185
      (x-2)² + (y-3)² = 185
      x² - 4x + 4 + y² - 6y + 9 = 185
      x² + y² - 4x - 6y - 172 = 0
4. x = y + √(x²+ a²)
   x – y = √(x²+ a²)
   (x – y)² x² + a²
   (x – y)² x² = a²
   ± √((x-y+x)(x-y-x) = a
   ± √(2x-y)(-y) = a
   ± √(y²- 2xy) = a
5. (²/₃ x+20)+⁵/₆ x+10º=90
   ⁹/₆ x+30=90
   ⁹/₆ x=60º
   x = 40º
   =Tan (x+20)
   =Tan 60 M1
6. CUBE
   

   	1	2	3	4	5	6
   1	2	3	4	5	6	7
   2	3	4	5	6	7	8
   3	4	5	6	7	8	9
   4	5	6	7	8	9	10

   1. P(6) = ⁴/₂₄ = ¹/₆
   2. P(6 or 9) = ¼
      P(6) = ⁴/₂₄
      P(9) = ²/₂₄
      ⁴/₂₄ + ²/₂₄
      ⁶/₂₄ = 1/4
7.      
   1. s = 8³ – 5 x 8² + 3 x 8 + 4
      512 – 320 + 24 + 4
      = 220m
   2. V = ^ds/_dt = 3t² – 10t + 3
      = 3 x 10² – 10 x 10 + 3
      300 – 100 + 3 = 197m
8. (x + 2) (x – 5 ) = 60
   x² – 5x + 2x – 10 = 60
   x² – 3x – 70 = 0
   x² – 10x + 7x – 70 = 0
   x (x – 10) + 7(x – 10) = 0
   (x – 10) (x +7) = 0
   x = 10
   x = -7
   Length 10 + 2 = 12m
9. Upper class limits 12.5, 15.5, 18.5, 21.5 24.5
   Cumulative frequency 3, 19 55, 86,100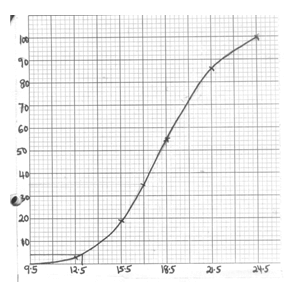
   
10.    
    
    1. Median = 50th 18.2 ± 0.15
    2. Leaves below 13 =4 leaves
       leaves below 17 =35 leaves
       leaves between 13 and 17 = 35-4=31
11.