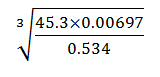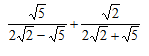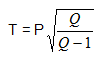Mathematics Paper 2 Questions and Answers - Form 4 End Term 1 Exams 2023

SECTION I (50 MARKS)
Answer all the questions from this section

1. Use logarithm to solve tables to evaluate (4 marks)
   

2. The length and breadth of a rectangular paper were measured to be the nearest centimeter and found to be 20cm and 15 cm respectively. Find the percentage error in its perimeter leaving your answer to 4 significant figures.      (3 marks)

3. Simplify the following surds leaving your answer in the form a+b√c(3 marks)
   

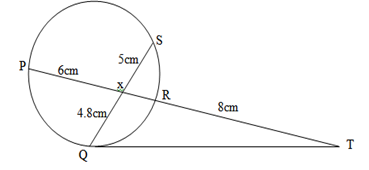
4. In the figure below QT is a tangent to the circle at Q. PXRT and QXS are straight lines. PX = 6cm, RT = 8cm, QX = 4.8cm and XS = 5cm.                                                   
   Find the length of QT       (3 marks)
   

5. Mary and Jane working together can cultivate a piece of land in 6 days. Mary alone can complete the work in 15 days. After the two had worked for 4 days Mary withdrew the services. Find the time taken by Jane to complete the remaining work. (3 marks)

6. The equation of a circle is given by   3x² + 3y² – 18x + 12y – 9=0. Determine the radius and the center of the circle.       (3 marks)

7. Make Q the subject of the formula   (3 marks)
   

8. Solve for x in the equation
   2sin² x – 1 = cos² x + sin x for 0⁰ ≤   x ≤ 360    (3 marks)

9. Solve for x in  (3 marks)
   

10. In a transformation, an object with area 4cm² is mapped onto an image whose area is 48cm² by a transformation matrix Find the value of y (3 marks)

11.  
    1. Expand (2 + 2y)⁵. (2 marks)
    2. Hence find the value of (2.02)⁵, correct to 4 decimal places when substitution for y is up to y⁴.            (2 marks)

12. A coffee blender mixes 6 parts of type A with 4 parts of type B. If type A costs sh 72 and type B costs him sh 66 per Kg respectively, at what price should he sell the mixture in order to make 5% profit? Give your answer to the nearest ten cents.                         (3 marks)

13. The data below represents the ages in months at which 11 babies started walking: 9,15 , 12, 9, 8, 13, 7, 11, 13, 14 and 10.
    Calculate the interquartile range of the above data       (3 marks)

14. Karimi deposited sh 45000 in a bank which paid compound interest of 12% per annum. Calculate the amount after 2 years to the nearest whole number.        (3marks)

15. Use tables of reciprocals only to work out (3 marks)
    

16. PQR is a triangle of area 9cm² . If PQ is the fixed base of the traingle and 6cm long draw it and describe the locus of point R. (3marks)

SECTION II (50 marks)
Answer only five questions from this section in the spaces provided

17. Pump R can fill an empty water tank in 6 hours while pump S can fill the same tank in 7 hours. On a certain day, when the tank was empty, both pumps were opened for 17 hours.
    1. Determine the fraction of the tank that was still empty at the end of the 17 hours. (4 marks)
    2. Pump R was later opened alone to completely fill the tank. Determine the time it took pump R to fill the remaining fraction of the tank. (2 marks)
    3. The two pumps R and S are operated by different proprietors. Water from the full tank was sold for Ksh 31 500. The money was shared between the two proprietors in the ratio of the quantity of water supplied by each.
       Determine the amount of money received by the proprietor of pump R (4 marks)
18. A rectangular plot measures 75 m by 36 m A lawn, rectangular in shape, is situated inside the plot with a path surrounding it as shown in the figure below.
    
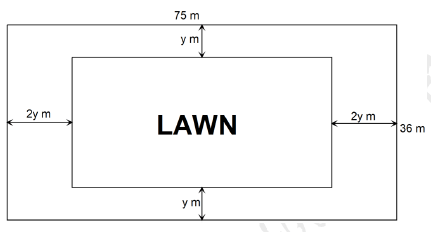
    The width of the path is ym between the lengths of the lawn and those of the plot and 2y m between the widths of the lawn and those of the plot.
    1. Form and simplify an expression in y for the area of the
       1. Lawn; (2 marks)
       2. Path. (1 mark)
    2. The ratio of the area of the path to the area of the lawn 3:2
       1. Form an equation in y and hence solve for y. (4 marks)
       2. Determine the perimeter of the lawn. (3 marks)
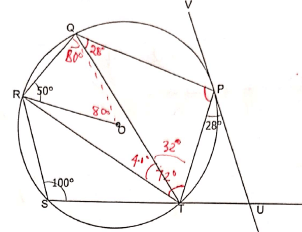
19. In the figure below, points P, Q, R, S and T lie on the circumference of a circle centre 0. Line UPV is a tangent to the circle at A. Chord ST of the circle is produced to intersect with the tangent at U. Angle UPT = 28º, ∠RST = 100° and ∠ORQ = 50°
    
    
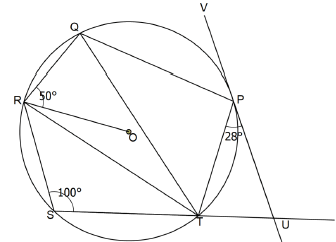
    1. Determine the size of:
       1. ∠PTR (3 marks)
       2. ∠PTO (3 marks)
    2. Given that PQ = 6 cm, ST=5.4 cm and TU=3.5 cm Calculate correct to 1 decimal place:
       1. The radius of the circle (2 marks)
       2. The length of line PU (2 marks)
20. The table below shows income tax rates in a certain year.
    

    Monthly taxable income in Kenya Shillings	Tax rates
    0 - 13458	10%
    13459 - 26351	15%
    26352 - 39244	20%
    39245 - 52137	25%
    52138 and above	30%

    In the year, the monthly earnings of Kaliech were as follows:
    Basic salary Ksh 75 500
    House allowance Ksh 13 600
    Kaliech contributes 12.5% of his basic salary to a pension scheme. This contribution is exempted from taxation. He is entitled to a personal tax relief of Ksh 2 400 per month.
    Calculate:
    1. Kaliech's monthly taxable income (2 marks)
    2. The tax payable by Kaliech that month. (6 marks)
    3. Kaliech's net pay that month. (2 marks)
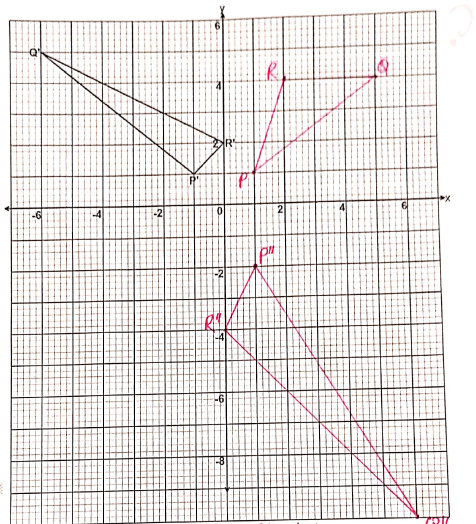
21. The vertices of the triangle shown on the grid are P'(-1,1), Q'(-6,5) and R'(0,2). Triangle P'QR' is the image of triangle PQR under a transformation whose matrix is (^-2₁ ¹₀)
    
    
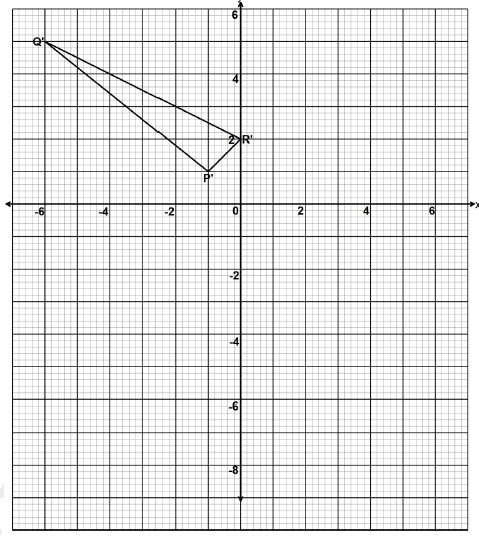
    1. Find the coordinates of triangle POR (4 marks)
    2. Triangle P'O'R" is the image of triangle P'O'R' under a transformation matrix (^-1₀ ⁰₂).
       Determine the coordinates of triangle P"Q"R". (2 marks)
    3. On the same grid provided draw triangles PQR and P'Q"R" (2 marks)
    4. Determine a single matrix that maps PQR onto P'O'R" (2 marks)
22. Workers in an institution commute from their homes to the institution. The table below shows the distances in kilometres, covered by the workers.
    

    Distance (km)	4-6	7-9	10-12	13-15	16-18	19-21	22-24
    Number of workers	4	15	21	k	13	9	5

    The mean distance covered was 13.4 km.
    1. Determine the value of k and hence the standard deviation of the distances correct to 2 decimal places. (6 marks)
    2. Calculate, correct to 2 decimal places, the interquartile range of the distances. (4 marks)
23.    
    1. Complete the table below giving the values correct to 1 decimal place.(2 marks)
       

       xº	0	30	60	90	120	150	180	210	240	270	300	330	360
       y= 3 sin(2/3x) –3 cos(2/3x)	-3	-1.8		1.1	2.4	3.5		4.2	3.8	3	1.8		-1.1
       y=1–2 sinx	1	0		-1		0	1	2	2.7			2	1

    2. On the grid provided and using the same axis, draw the graphs of y = 3 sin(²/₃x) - 3cos(²/₃x) and y=1-2cosx for the range 0° ≤ x ≤ 360° (4 marks)
       
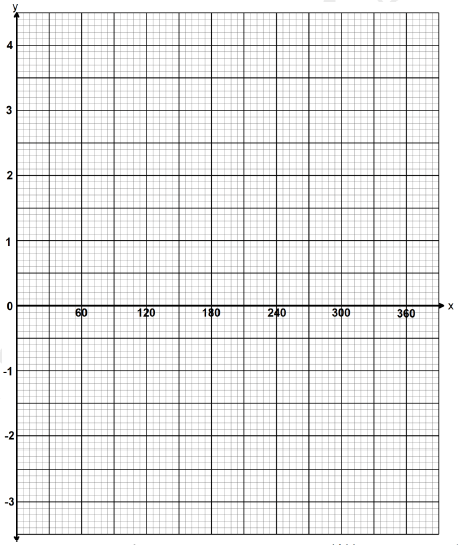
    3. Using the graphs in part (b):
       1. Find the values of x for which sin(²/₃x) = ½ + cos(²/₃x) (2 marks)
       2. Determine the range of x which 3 sin(²/₃x) -3 cos(²/₃x) > 1 - 2cosx (2 marks)
24. A particle moves along a straight line such that its displacement s metres after t seconds is given by s = t³ - pt² + qt + 4. Given that its velocity, v after 5 seconds was 28 m/s and its acceleration, a after 5 seconds was 20m/s².
    1. Determine the value of p and q (5 marks)
    2. Find the values of t when the particle is momentarily at rest. (3 marks)
    3. Calculate the displacement of the particle at t = 5 seconds (2 marks)

MARKING SCHEME

SECTION II

1.  
   1. In 1h R fills ⁴/₅, S fills ²/₁₅
      In 1h both fill ⁴/₂₅ + ²/₁₅ = ²²/₇₅
      In 1⁷/₈h both fill ¹⁵/₈ x ²²/₇₅ = ¹¹/₂₀
      fraction empty = 1 - ¹¹/₂₀
   2. = ⁹/₂₀
      ⁴/₂₅ is filled in 1hr
      ⁹/₂₀ is filled in ⁹/₂₀ x ²⁵/₄ x 1
      2hrs 48mins 45secs/ 213/16hrs
   3. fraction of tank filled S
      1h = ²/₁₅
      17/8 = ¹⁵/₈ x ²/₁₅ = ¼
      fraction filled by R = 1 - ¼ = ¾
      amount for R = ¾ x 31500º)
2.  
   1.  
      1. area = (75-4y)(36-2y)
         2700-144y-150y+8y²
         2700-294y+8y²
      2. (75 x 36) - (2700 - 294y + 8y²)
         2700 - 2700 + 294y - 8y²
         294y - 8y² 
   2.  
      1. (294y - 8y²) = ³/₂(2700 - 294y + 8y²)
         588y - 16y² = 8100 - 882y + 24y²
         40y² - 1470y + 8100 = 0
         4y² - 147y + 810 = 0
         y = 147±√(-147)² - 4 x 2 x 810
                              2 x 4
         y =147 ±123
                     8
         y = 33.75m or y =3m
      2. length = 75 - 4 x 3 = 63m
         width = 36 - 2 x 3 = 30m
         P = 2(63 + 30)
         = 186m
3. 
      
   1.          
      1. ∠PQT = 28º(alternate segment theorem)
         ∠RQT = 180 - 100 = 80º (opp ∠s of cyclic quad add to 180)
         ∠PTR = 180-(80+28)
      2. ROQ = 180 -(50x2)=80º 
         QTR = ⁸⁰/₂ = 40º
         PTQ = 72 - 40 = 32º
   2.  
      1. ⁶/_sin32º = 2R
         R = 5.7cm
      2. (PU)² = TU.SU
         PU = √3.5(3.5 + 5.4)
         = 5.6cm
4.  
   1. ⁸⁷⁵/₁₀₀ x 75500 + 136000
      Ksh 79662.50
      OR
      75500 + 13600 - 12.5/100 x 75500
      Ksh 79662.50
   2. 1st slab 13458 x 10/100 = 1345.8
      2nd slab 12893 x 15/100 = 1933.95
      3rd slab 12893 x 20/100 = 2578.6
      4th slab 12893 x 25/100 = 3223.25
      5th slab 27525.5 x 30/100 =  8257.65  
                                                   17339.25
      17339.25 - 2400
      Ksh 14939.25
   3. 75500 + 13600 - 12.5/100 x 75500 + 14939.25
      Ksh 64,723.25
      or 79662.50 - 14939.25
5.  
   1. 
      
   2.  
      
   3.  
      
      
      
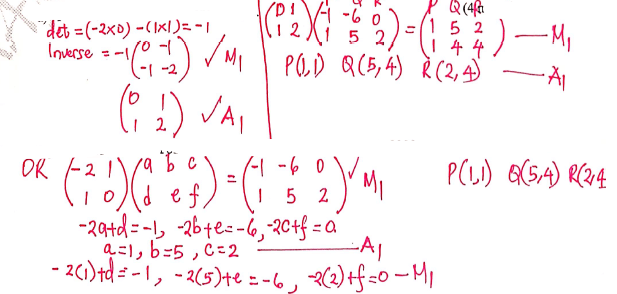
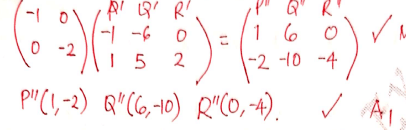
   4. a+b = 1
      5a+4b=6
      5a+5b=5
      5a+4b=6
      b = -1
      a = 1+1=2
      c+d = -2
      5c+4d = -10
      5c+5d=-10
      5c+4d= -10
      d = 0
      c= -2
      Matrix = (2-2 -10)  
6.  
   1.  
      

      Distance (km)	4-6	7-9	10-12	13-15	16-18	19-21	22-24
      Number of workers	4	15	21	k	13	9	5
      c.f	4	19	40	58	71	80	85

      
      

      class	f	x	fx	fx2
      4-6	4	5	20	100
      7-9	15	8	120	960
      10-12	21	11	231	2541
      13-15	k	14	14k	3528
      16-18	13	17	221	3757
      19-21	9	20	180	3600
      22-24	5	23	115	2645
      	85			1731

      s.d = √17131 - 13.4²
                    85
      = 4.69
      x =∑fx = 887 + 14k = 13.4
            ∑f        67+k
      k = ^10.8/_0.6 = 18
   2. Q =¼ x 85 = 21.25
      9.5 + (21.25 - 19) x 3
                      21
      9.821
      Q3 =¾ x 85 = 63.75
      15.5 + (63.75 - 58) x 3
                        13
      = 16.827
      Q - Q1 = 16.827 - 9.821 = 7.01    
7.  
   1.  
      

      xº	0	30	60	90	120	150	180	210	240	270	300	330	360
      y= 3 sin(2/3x) –3 cos(2/3x)	-3	-1.8	-0.4	1.1	2.4	3.5	4.1	4.2	3.8	3	1.8	0.4	-1.1
      y=1–2 sinx	1	0	-0.7	-1	-0.7	0	1	2	2.7	3.0	2.7	2	1

   2.  
      
   3.  
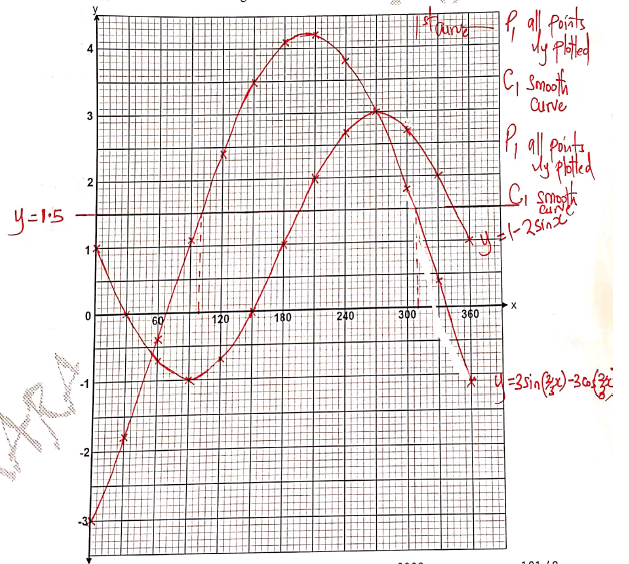
      1. sin(²/₃x) - cos(²/₃x) = ½
         3sin(²/₃x) - 3cos(²/₃x) = ³/₂
         3sin(²/₃x) - 3cos(²/₃x) = y
         y = ³/₂
         x = 97º to 101º or 307º to 311º
      2. 54º < x < 270º
8.  
   1. v = ^ds/_dt = 3t² - 2pt + q
      3(5)² - 2p(5) + q = 28
      75 - 10p + q = 28
      -10p + q = -47
      a = dv/dt = 6t - 2p
      6(5) - 2p = 20
      -2p = -10
      p = 5
      -10(5) + q = -47
      q = 3
   2. s = t³ - 5t² + 3t + 4
      v = ^ds/_dt = 3t² - 10t + 3 = 0
      3t² - 9t - t + 3 = 0
      3t(t-3) -1(t-3)=0
      (3t-1)(t-3) = 0
      t = ¹/₃ or t = 3
   3. s = 5³ - 5(5)² + 3(5) + 4
      s = 125 - 125 + 15 + 4
      = 19m