Questions

1. The size of an interior angle of a rectangular polygon is 6 ½ times that of its exterior angle.
   Determine the number of sides of the polygon.
2. The sum of interior angles of two regular polygons of sides n and n + 2 are in the ratio 3:4.
   Calculate the sum of the interior angles of the polygons with n sides
3. The area of a rhombus is 60cm2. Given that one of its diagonals is 15cm long. Calculate the perimeter of the rhombus.
4. In the figure below AE is parallel to BD. BC = BD, AB = 7.25cm, AE = 15.25cm and ED = 5.25 cm
   
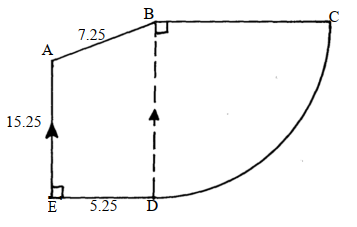
   Find the perimeter of the figure .
5. The figure below shows a trapezium ABCD in which side AB is perpendicular to both AD and BC. Side AD=17cm, DC=10cm
   
   
   1. What is the length of side AB
   2. Find the value of cos(90^o – x^o) in the form ^a/_b where a and b are integers
6. The size of an interior angle of a regular polygon is 3x^o while its exterior angle is (x-20)^o.
   Find the number of sides of the polygon
7.  
   
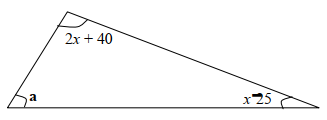
   In the figure above, angle a is half the sum of the other angles. Evaluate the triangle
8. The sum of the interior angles of an n-sided polygon is 1260^o. Find the value of n and hence deduce the polygon
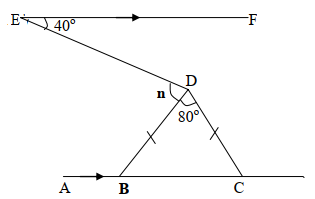
9. Giving reason, find the angle marked n
   
   
10. Solve for y in the equation 125^y+1 + 5^3y = 63⁰
11. The interior angle of a regular polygon is 108o larger than the exterior angle. How many sides has the polygon?
12. The interior angle of a regular polygon is 4 times the exterior angle. How many sides has the polygon
13. In the figure below ABCD is a trapezium with DC parallel to AB. DC = 5cm, CB = 4cm, BD = 8cm and AB = 10cm
    
    Calculate:
    1. the size of angle BD
    2. the area of triangle ABD
14. In the figure below, DE bisects angle BDG and AB is parallel to DE. Angle DCF = 60^o and angle CFG = 100^o
    Find the value of angle:-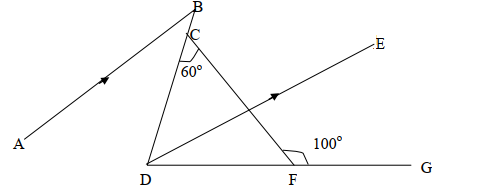
    
    
    1. CDF
    2. ABD
15. The size of an interior angle of a regular polygon is 4x^o, while its exterior angle is (x – 30)^o
    Find the number of sides of the polygon
16. The sum of interior angles of a polygon is 1440^o. Find the number of sides of the polygon hence name the polygon
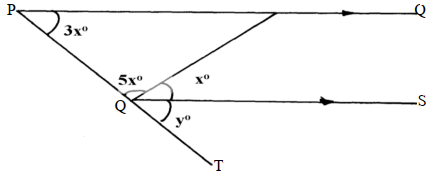
17.  In the figure below PQ is parallel to RS. Calculate the value of x and y
    
    
18. The interior angle of a n-sided regular polygon exceeds its exterior angle by 132^o.Find the value of n
19. The sum of angles of a triangle is given by the expression (2a+b)^o while that of a quadrilateral is given by (13a - b)^o. Calculate the values of a and b (4 mks)
20. The figure below represents a quadrilateral ABCD. Triangle ABX is an equilateral triangle. If <ADX = 50^o , find <AXD with <BAD = 90^o (2 mks)
    
21. Wanjiku is standing at a point P, 160m south of a hill H on a level ground. From point P she observes the angle of elevation of the top of the hill to be 67^o
    1. Calculate the height of the hill (3 mks)
    2. After walking 420m due east to the point Q, Wanjiku proceeds to point R due east of Q, where the angle of elevation of the top of the hill is 35^o. Calculate the angle of elevation of the top of the hill from Q (3 mks)
    3. Calculate the distance from P to R (4 mks)

Answers

1. Let the exterior ∠be x
   6.5x + x = 180
   7.5x = 1800
   x = 24
   No. of sides = ³⁶⁰/₂₄
   = 15 sides.
2. (2n – 4) 90 =  3
   (2(n+2) - 4)90 4
   2n – 4 = 3
   2n          4
   8n – 16 = 6n
   2n = 16
   n = 8
   (2(8) – 4) 90
   = 12 x 90 = 1080
3. 15 b = 60
   2   2
   15b = 60 x 4
   b = 16cm (diagonal)
   = √8² + 7.5²
   ∴per = 4 √8² + 7.5²
   = 43.86cm
4. x² = 7.25² – 5.25²
   x = √7.25² – 5.25²
   = 52.5625
   27.5625 -
   √25
   = 5cm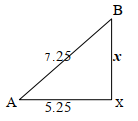
   
   BC = 15.25 + 5 = 22.25cm
   Arc CD = ⁹⁰/₃₆₀ X 3.142 X 2 X 22.25
   = 34.65475
   Perimeter = AB + BC + CD + DE + EA
   = 15.25 +7.25 + 22.25 + 34.95 + 5.25
   = 84.95cm
5. AB² = 102 – 82= 100 – 64
   AB² = 36
   AB = 6cm
   Cos (90^o – x^o) 8/10 = 4/5
   
6. x -20 + 3x = 180^oC
   4x = 200
   x = 50^o
   
7. 2x + 40 + x – 25
   3x + 15 + 9 = 180
    3x + 15 = 29
   9 = ½ (3x + 15)
   3x + ^3x/₂ = 180 -15-¹⁵/₂
   x = 35^o
   x = 35 = 10^o
   ½ ( 10 + 110) = 60^o
8. 1260 = 14rt ∠s
   90
   Sum of interior ∠s
   (2n -4) rt ∠s
   2n-4 = 14
   n = 9
   9 sided polygon
9. N = 50 + 40 = 90^o
   Alternative angles
10. 53(y+1) + 53y = 630
    Let x = 53y
    53 x 53y + 53y =630
    125x + x = 630
    x = 5
    53y = 51
    3y = 1
    y =¹/₃
11. 360/_n + ¹⁰⁸/_n = 180 - 360
    360 + 108n = 180n – 360
    -72n = -720
    n = 10
12. Let exterior angle be x
    ^4x/₄ = 180^o/₄
    x = 45^o
    n=360
    Exterior angle
    n = ³⁶⁰/₄₅
    = 8 sides
13.   
    1. Let ∠BDC = ø
       A²= 5²+ 8² – 2 x 5 x 8 cos ø
    2. Area of ABD
       = ½ x 8 x 10 sin 24°9¹
       = 40 x 0.4091
       = 16.36cm³
       
14.  
    
    1. ∠CDF = 100-60=40^o (exterior angle of a Δ)
    2. ∠BDE = 20^o (DE is bisector of BDG)
       ∠ABD = 20^o (alternate angles)
15. 4x + x – 30 = 180
    5x = 210°
    x = 42
    (x - 30)n = 360°
    12n = 360°
    n = 360°/₁₂
    n = 30
16. 180(n-20) = 1440
    n - 2 = ¹⁴⁴⁰/₁₈₀ = 8
    n = 10
    Decagon
17. ∠PQR =∠SRT = x (Alt ∠SPQ //RS)
    ∴5x + 3x + x = 180° <’s of 
    9x = 180°
    X = 20°
    ∴5 x 20 + y = 180
    y = 180 – 120 = 60
18.  Let the interior ∠be x and exterior be y
    ∴ x + y = 180
    +
    x – y = 132
    2x = 312
    
    x = 156
    y = 180 – 156 = 24^o
    No. of sides (n) = 360^o/₂₄= 15
    = 15 sides

---

Download Angles and Plane Figures Questions and Answers - Form 1 Topical Mathematics.

Tap Here to Download for 50/-

---

Get on WhatsApp for 50/-

---

Join our whatsapp group for latest updates