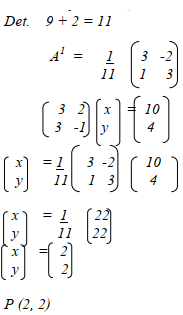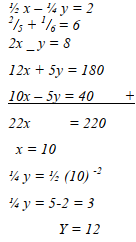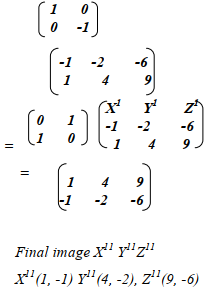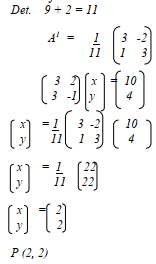Matrices Questions and Answers - Form 3 Topical Mathematics

Questions

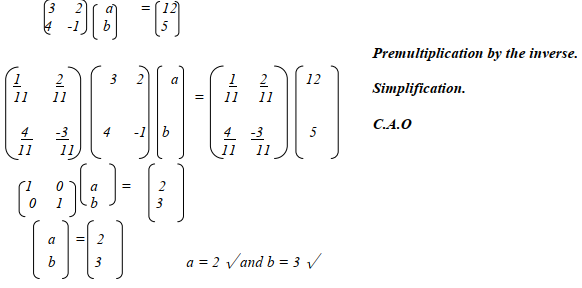
1. Given that A is and A^-1 is
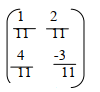
   Find the value of a and b in the expression: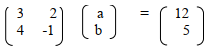
   (3 mks)
2. Solve for the unknowns given that the following is a singular matrix.
   
   
3. Given that A = and B = and that C = AB, find C^-1
4. B is a matrix  and C is the matrix 
   If A is a 2 x 2 matrix and A x B = C. determine the matrix A.
5. An object of area 20 cm2 undergoes a transformation given by the matrix  followed by  find the area of the final image
6.  Find the matrix B such that AB = I and A = Hence find the point of intersection of the lines 3x + 2y = 10 and 3y – 4 = x.
7. Given that P =  and Q =  find the matrix product of PQ. Hence solve the simultaneous eqution below
   2x – 3y = 5
   - x + 2y = – 3
8. Solve for x and y in the following matrix equation using elimination method
   
   
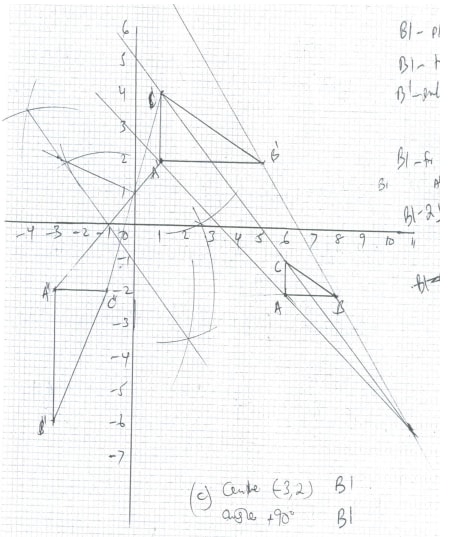
9. A triangle XYZ , X (-1, -1) , Y (-2, -4) Z (-6 , -9) is reflected in the line X axis followed by a reflection in line X= Y. Find the image of the final image
10. Triangle ABC is the image of triangle PQR under a transformation M =  where P, Q, R map onto A, B, C respectively.
    1. Given the points P (5, -1) Q (6, -1) and R(4, - 0.5) draw the triangle ABC on the grid provided.
    2. Triangle ABC in (a) above is to be enlarged by scale factor 2 with centre at (11, - 6) to map onto A¹B¹ and C¹. Construct and label triangle A¹B¹ and C¹ on the same grid.
    3. By construction, find the coordinates of the centre and the angle of rotation which can be used to rotate triangle A^IB^IC^I onto triangle A^IIB^IIC^II whose coordinates are (-3, -2) , (-3, -6) and (-1, -2) respectively.
11. Triangle ABC with an area of 15 cm² is mapped onto triangle A^IB^IC^I using matrix M = . Find the area of triangle A^IB^IC^I.
12. T is a transformation represented by the matrix  under T a square whose area is 10cm² is mapped onto a square of area 110cm². Find the possible values of X
13. Triangle A¹B¹C¹ is the image of ΔABC under a transformation represented by the matrix
    M = 
    If the area of triangle A¹B¹C¹ is 54cm². Determine the area of triangle ABC
14. Find the matrix B such that AB = I and A =  . Hence find the point of intersection of the lines 3x + 2y = 10 and 3y – 4 = x

Answers

1.  
   
2. (x-3) – (2x) = 0
   x-3-2x = 0
   -2x + x – 3 = 0
   -x -3 = 0
   x=3
3.  
   
   Determinant = + 65 – 49 = 16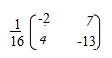
   
   
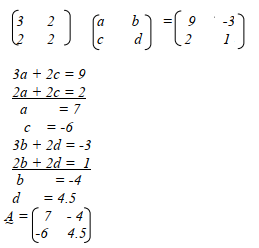
4.  
   
   
   
5. 20x (-3 - -8)
   100 area of 1^st image.
   100 x (4 - -3)
   700 area of 2^nd image
6.  
   
7.  
   
8.  
   
9.  
   
10.  
    
    
    
    
11. Det 2 - -3 = 5
    Area of A^IB^IC^I = 5 x 15
    = 75 cm²
12. A.S.F = 110 = 11
                 10
    5X (X) - -6 = 11
    5X² + 6 = 11
    5x² = 5
    X² = 1
    X = ±1 
13. Area of the image = Area of the object x Det.
    Det. (∆) = 15 – 18 = -3
    54 cm² = A x -3
    54 cm² = A
     3
    Area of ∆ ABC = 18 cm²
14.