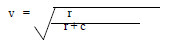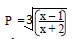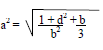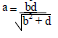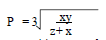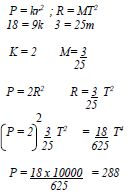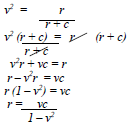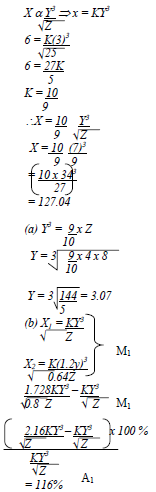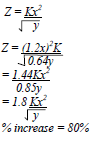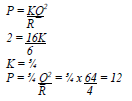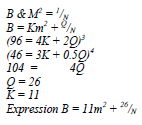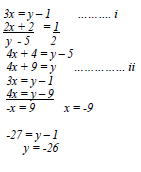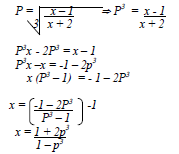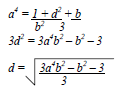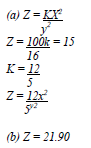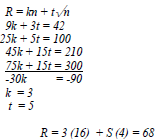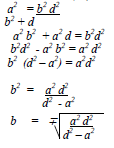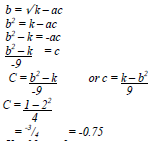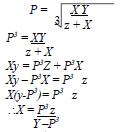Formulae and variation Questions and Answers - Form 3 Topical Mathematics

Questions

1. P varies as the square of R. R. varies as the square of T. When P = 18, R = 3 and T = 5. Express P in terms of T hence find P when T = 10.
2. Make r the subject of the formula.
   
3. X varies as the cube of Y and inversely as square root of Z, X = 6 when Y = 3 and Z= 25.
   1. Find;
      1. An expression connecting X,Y,Z
      2. X when Y = 7 and Z = 9
      3. Y when X = 8 and Z = 16
   2. If Y is increased by 20% and Z is decreased by 36%, find the percentage increase in X
4. Make b the subject of the formula;
   K = ab
        b –a
5. A quantity Z varies directly as the square of x and inversely as the square root of y. If x increases by 20% and y decreases by 36%, find the percentage change in Z.
6. A quantity P varies directly as the square of Q and inversely as quantity R. If P = 2 when Q = 4 and R=6, find P when Q = 8 and R= 4.
7. B varies partly as the square of M and partly as the inverse of N. B,M and N are such that when M=2, N= ½ , B=96 while when M= 3 , N=2, B = 46. Write an expression for B in terms of M and N.
8. Solve for x and y.
   3x    = 1
   y - 1
   (2x + 2) : (y – 5) = 1 : 2
9. Make x the subject of the formula.
   
10. Make d the subject of the formula given that:-
    
11. Z varies jointly as the square of x and inversely as the square of y. When x = 10 and
    y = 4 then z = 15.
    1. Find z in terms of x and y
    2. Find the value of x when z = 8 and y = 12
12. A quantity R partly varies as n and partly as the square root of n. When n = 9 R = 42 and when n = 25 R = 100. Find R when n = 16.
13. Make b the subject of the formula.
    
14. P varies party as Q and partly as the square root of Q. When Q = 4, P = 22 and when
    Q = 9, P = 42. Find the value of P when Q = 25.
15. Make C the subject of the formula
    b = √(k-aC)
    hence find the value of C when K= 1, a = 4 and b = 2
16. The velocity of water flowing through a pipe is inversely proportional to the square of the
    radius of the pipe. If the velocity of the water is 30cm/s when the radius of the pipe is 2cm. Find the velocity of water when the radius of the pipe is 4cm.
17. Make x the subject of the formula.
    
18. Three quantities x, y and z are such that x varies partly as y and partly as the inverse
    of the square of Z . When x = 6, y = 3 and z= 2. When x = 8, y = 5 and z= 1. Find the
    value of x when y = 10 and z= 8.
19. The resistance of an electrical conductor is partly constant and partly varies as the temperature. When the temperature is 20^oC, the resistance is 55 ohms. When the temperature is 28^oC, the resistance is 58 ohms. Find the resistance when the temperature is 60^oC

Answers

1. 
   
2. 
   
3. 
   

4. K ( b-a) = ab
   Kb – ka = ab
   Kb – ab = ka
   B(k-a) = ka
   B =    ka 
          K –a

5. 
   
6. 
   
7. 
   
8.  
   
9. 
   
10. 
    
11.  
    
12.  
    
13.  
    
14. P = KQ + m√Q
    22 = K (4) + m(2)……………(1)
    42 = K(g) + n(3)……………(2)
    22= 4K + 2m
    42 = 9K + 3m
    3(22) = 3(4K) + 3(2m)
    2(42) = 2(9K) + 2(3)
    66 = 12k + 6m
    84 = 18K + 6m
    18= 6k = k=3
    22 = 4(3) + 2m
    22-12 = 2m
    20 = 2m
    M = 10
    = 3(25) + 10(5)
    = 75 + 50
    = 125
15. 
    
16. V = 30, r = 2
    K = Ur²
    = 30 x 22 = 120
    When r = 4
    V = ¹²⁰/₄₂ = 7.5m/s
17. 
    
18.  
    
19. R = m + nI
    55 = M + 20n……(i)
    58 = m + 28n…….(ii)
    -3 = -8n
    n = ³/₈ = 0.375
    55 = m + 60/8
    m =55 -7.5 => m = 47.5
    R = 47. 5 + 60 X 3/8
    R = 70 ohms