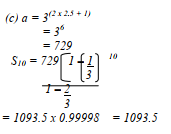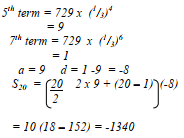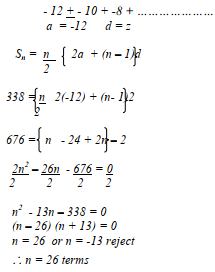Sequences and Series Questions and Answers - Form 3 Topical Mathematics

Questions

1. The area covered by Mau forest is 40,000 km² at present. If the human encroachment rate is estimated to be 2% every 10 years. Calculate the area of the forest encroached in 30 years.
2. Three consecutive terms of geometric progression are 3^{2x + 1}, 9^x and 81 respectively. Calculate:
   1. The value of x
   2. Find the common ratio
   3. Calculate the sum of the first 10 terms of this series
   4. Given that the fifth and the seventh terms of this G.P forms the first two consecutive terms of arithmetic sequence, calculate the sum of the first 20 terms of this sequence
3.  How many terms of the sequence -12 + -10 + -8 .....should be added to give a sum of 338?
4. An arithmetic progression whose first term is 2 and whose nth term is 32 has the sum of its n terms equal to 357. Find n
5. In the figure OACB is parallelogram in which M is the mid- point of AC and OM produced meets BC also produced at X.
   
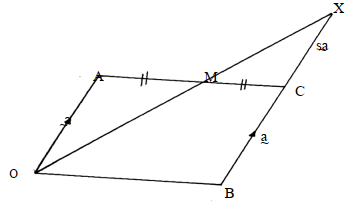
   Given OA = a and OB = b
   1. Express OC in terms of a and b
   2. Find the values of r and s such that OX = rOM and CX = sBC
   3. Hence determine the ratio BC:BX
6. For the series 29 + 23 +..... + (-91), find;
   1. The number of terms in the above series
   2. The sum of the series
7. 1. Given that 5, a, b, and 7 are in arithmetical progression, find the value of a and b
   2. If 5, P, Q , ¹³⁵/₈ are in geometrical progression. Find the value of P and Q
   3. Prove that the sum of the first 12 terms of the first series in (a) is approximately equal to the sum of the first 6 terms of the second series (b) above
8. An aeroplane flew East for 640km then turned and flew on a bearing of 050o. After 2.5hrs flying at 324km/hr, it was necessary to fly to the original point because of technical hitch. How much shorter is it going to cover flying straight to the starting point than retracing its former route?
9. A ball falls vertically from a height of 15m. Each time it bounces back to 50% of the height achieved on the previous bounce. Find the distance covered after 6 such bounces
10. Find the sum of the first 51 terms of the series: -22, -19, -16...................................
11. Olunga saves shs.100 on his son’s first birthday. He saves shs.200 on the second birthday and Shs.400 on the third birthday and so on doubling the amount on every birthday. How much will he be saving on the boy’s 10th birthday.
12. A self-help group intended to purchase a dry cleaning machine worth shs.720,000. The members were required to contribute equal amounts to pay for the machine. The group recruited 20 more members consequently, each member paid shs.3000 less that what he would have contributed.
    1. find the original number of members
    2. find the amount required from each member to contribute after the recruitment
13. Find the number of terms in the following sequence
    8, 4, 2, ½ …….., ¹/₅₁₂
14. An arithmetic progression has the first term a and the common difference d
    1. Write down the third, ninth and twenty fifth terms of the progression in terms of a and d
    2. The arithmetic progression above is increasing and that the third, ninth and twenty fifth terms form the first three consecutive terms of a geometric progression. The sum of the seventh and twice the sixth terms of the arithmetic progression is 78.
       Calculate:
       1. The first term and common difference of the arithmetic progression
       2. The sum of the first nine terms of the arithmetic progressionn
15. The difference between the fourth and the seventh terms of an increasing arithmetic progression

Answers 

1.  
   
2.  
   
   1. 9^x       =     81
      3^{2x + 1}         9^x
      9^2x = 34(3^{2x + 1})
      3^4x = 3^{4 + 2x + 1}
      3^4x = 3^{2x + 5}
      4^x = 2^{x + 5}
      2x = 5
      x = 2.5
   2.  
      Common ratio = 81 
                             92.5
      = 1 
         3
   3.   
      
   4.  
      
3.  
    
4.   
   
   
5.  
   1. OC = OB + BC = a + b
   2.  OM = OA + AM = a + ½ b
      Given OX = rOM
      = r(a + ½ b)
      From ΔOBX
      Ox = OB + BX
      = OB + BC + CX
      = b + a + sa
      = (1+s) a +b
      ∴ r(a + ½ b) = (1 + s) a + b
      Comparing coefficients of a and b
      r = 1 + S
      and ½ r = 1⇒r = 2
      Substitute for r = 2 ⇒2 = 1 + s ⇒s = 1
   3. Now BX = BC + Cx
      = a + a = 2a
      ∴BC:BX = 1:2-91 = 29 + (n-1) x -6
6.  
   1. -120 = -6n + 6
      6n = 126
      n = 21
   2. S₂₁ = ²¹/₂ [(2 x 2a) + (20 x -6)]
      = 21 x -62
              2
      = -651
7. d = p - 5 ….....(i)
   d = q – p .………(ii)
   0 = 2p -q – 5
   0 = 7 – 2q + p
   - p + 2q = 7
   2p – q = 5
   -2p + 4q = 14
   2p – q = 5
   3q = 19
   q =¹⁹/₂
   p=2q – 7
   ³⁸/₂ – 7
   p=¹⁷/₈
   S = n {2a + (n-1)d}
         2
   =¹²/₂ (10+11 x ²/₃)
   = 6 (10+²²/₃) = 104
   S_n= a(rⁿ-1) = S(1.5-6)
   r - 1 1.5 – 1
   = 5 x (1.5 – 1) = 103.90
   0.65 = 10.4
8.  a + a + d = 10………………(i)
   10{2a + 9d}= 210……………..(ii)
    2
   2a+ d =10
   2a + 9d = 42
           8d = 32
             d= 4
   T₁ = 3 +6(4)
   = 3 + 24
   = 27
9. S₆ = 15 (1-0.56)
              1 - 0.5
   = 29.5314metres
10. S_n = n {2a + (n-1)L
            2
    S51 = 51 (2x -22) + (51 -1)3
               2
    = 2703
11. 100 + 200 + 400 + 800 + 1600 + 3200 + 6400 + 12800 + 25600 + 51200
    200 =  400 = 800
    100     200     400
    = 51200 99600 108200 110,600
    25600    6400      1600        700   
    76800 105,000 109,800    111,300
    12800     3,200        800   
    99,600  108,200   110,600
    = 111300
12. 1. Let n be the initial members
       Each to contribute ⁷²⁰⁰⁰⁰/_n
       New membership n + 20
       Contributions: 720000
                             n + 20
       720000 – 720000 = 3000
           n          n + 20
       720000(n + 20) – 720000n= 3000n(n + 20)
       4800 = n(n + 20)
       n²+ 20 – 4800 = 0
       n²+ 80n – 60n – 4800 = 0
       n(n + 80) – 60(n + 80)= 0
       (n-60) (n + 80) = 0
       n = 60
       Original members = 60
    2. Contributions required before recruitment
       = 720000
             60
       = 120000
       After requirement = 720000
13. n^th term is ar^n-1
    a = 8, r = ½
    n^th term = ¹/₅₁₂
    8(½)^n-1 = ¹/₅₁₂
    8(½)^n-1 = 2^-9
    (½)^n-1 = 2^-9 ÷ 2³
    (½)^n-1 = 2^-12 = (½)¹²
    n^-1= 12
    n = 13
14. 1. 3^rd a + 2d
       9^th a + 8d
       25^th a + 24d
       a + 2d =  a + 8d 
       a + 8d    a + 24d
       (a +2d) (a +2d) = (a + 8d) (a +8d)
       a2 + 26da + 48d2 = a2 + 16da + 64d²
       10da = 16d²
       10d      10d
       a = 1.6d………….(i)
       (a + 6b) + 2(a+5d) = 78
       3a + 16d = 78…………………(ii)
       But a = 1.6d
       ∴ (3x1.6d) +16d = 78
       4.8d + 16d = 78
       4.8d + 16d = 78
       20.8 = 78  
       20.8   20.8
       Common distance d= 3.75
       a=1.6 x 3.75
       first term a = 6
    2. Sn = ⁿ/₂ (2a + (n-1)d)
       Sa = ⁹/₂ ((2x6) + (9-1)3.75)
       =⁹/₂ (12 + 30)
       ⁹/₂ x 42= 189
15. T₄ = a + 3d
    T₇ = a + bd
    (a + 6d) – (a + 3d) = 12
    3d = 12
    d = 4
    But a = 9
    S5 = ⁵/₂ 2(9) + 4 (4)
    = ⁵/₂ (18 + 16)
    = ⁵/₂ x 34
    = 85