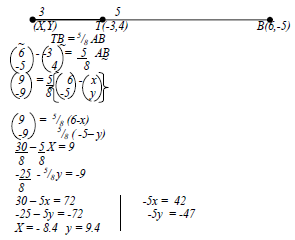Vectors 2 Questions and Answers - Form 3 Topical Mathematics

Questions

1.  
   
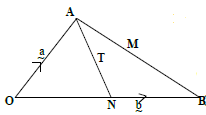
   In the figure alongside OA = a , OB = b. T lies on AN such that AN : TN = 13:6. M lies on AB such that AM:MB=1:3 and N lies on OB such that OB:BN = 7:-5.
   1. Express in terms of a and b in the simplest form.
      1. AN
      2. AT
      3. AM
   2. Show that O, T and M are collinear and state the ratio of OT: TM
2. A point (-3, 4) divides AB internally in the ratio 3:5. Find the coordinates of point A given that point B is (6, -5)
3. Given that O is the origin, OA = 3i + 2j – 4k and OB = 6i + 11j + 2k. If x divides AB in the ratio 1:2, find the modulus of OX to 2d.p
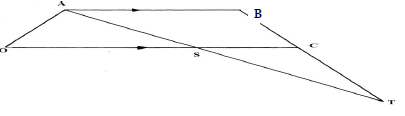
4. In the figure OABC is a trapezium in which 3 AB = 2OC. S divides OC in the ratio 2:1
   and AS produced meets BC produced at T.
   
   Given that OC = 3c and OA = a
   1. Express AS and BC in terms of a and c
   2. Given further that AT = hAS and BT = kBC where h and k are constants
      1. Express AT in two ways in terms a, c , h and k
   3. The obtuse angle between the lines PQ
   4. Hence find the ratio BT: BC
5. 
   
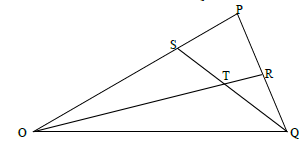
   In the figure above, OPQ is a triangle in which OS = ¾ OP and PR: RQ = 2 : 1. Lines OR and SQ meet at T.
   1. Given that OP = P and OQ = q, express the following vectors in term of p and q
      1. PQ
      2. OR
      3. SQ
   2. You area further given that ST = mSQ and OT = nOR. Determine the values of m and n.

Answers

1.  
   1.  
      1. AN = OA + ON
         = -a + ²/₇b
         = ²/₇b - a
      2. AT = ⁷/₁₃AN
         ⁷/₁₃ (-a + ²/₇b)
         ²/₁₃b - ⁷/₁₃a
      3. AM = ¹/₄AB
         = ¹/₄ (AO + OB)
         = ¹/₄ (b - a)
   2. OT = OA + AT
      = a + (²/₁₃b - ⁷/₁₃a)
      = ²/₁₃(3a + b)
      OM = OA + AM
      = a + (-¹/₄a + ¹/₄b)
      =³/₄a + ¹/₄ b
      =¹/₄(3a + b)
      OT = 2/13 (3a + b)
      OM     1/4 ( 3a + b)
      OT = ⁸/₁₃ OM
      Or OM = ¹³/₈OT
      Since OT = ⁸/₁₃OM
      Then OT : TM = ⁸/₁₃ : ⁵/₁₃
      = 8 : 5
2. 
   
3. OX = ²/₃(3i + 2j – 4k) + ¹/₃(6i + 11j + 2k)
   = 2i + 4j – ⁸/₃k + 2i + ¹¹/₃j + ²/₃
   = 4i + 5j -2k
   10x1 = √(16 + 25 + 4)
   = 6.71units
4. 1. AS = AO + OS
      = -a + 2(3c)
      = 2 c – a…………
      BC = BA + AC
      = a - b + AC
      But AC = AO + OC = -a + 3c
      = 3c – a……….
      AB + ²/₃OC = ²/₃ 3 c = 2 c
      BA = 2 c…….
      BC = -12c +3c – a = c -a.
   2.  
      1. AT = hAS = h(2c –a)
         = 2hc -ha
         AT = AB + BT = 2c + K ( c -a)
         = 2c + Kc – Ka
         = ( 2 + k)c – Ka
      2. 2 + K = 2h
         (i) K = h
         (ii) 2 + h = 2h
         2 = 2h - h
         2 = h, K = 2
   3. BT : BC
      BT = 2 BC
5.  
   1.  
      1. PQ = PO + OQ
         = P + q or q – p
      2. OR = OP + PR
         = P + ²/₃PQ
         = P + ²/₃(q – p)
         = P + ²/₃q - 2p
         = ¹/₃p + ²/₃q
      3. SQ = SO + OQ
         = -³/₄OP + OQ
         = -³/₄p + q or q – ³/₄p
   2. Express OT in two different ways:
      Given OT = nOR
      = n (¹/₃P + ²/₃q)
      = ⁿ/₃p + ²ⁿ/₃q
      From ΔOST,
      OT = OS + ST
      = ³/₄OP + MSQ
      = ³/₄P + M (-³/₄P +q)
      = (³/₄ - ³/₄m) p + mq
      ∴ ⁿ/₃p + 2nq = (³/₄ - ³/₄m) p + mq
      Compare the coefficients of p and q
      ⁿ/₃ = ³/₄ - ³/₄m
      4n = 9 – 9m
      4n + 9m = 9 ………………..eq (1)
      ²/₃n = m
      m = ²/₃n …………….eq. (2)
      Substitutes form in equation (1)
      4n + 9 (²/₃n) = 9
      4n + 6n = 9
      10n = 9
      n = ⁹/₁₀
      Substitute for n in equation (2)
      m = ²/₃ x ⁹/₁₀ = ³/₅