Questions
-
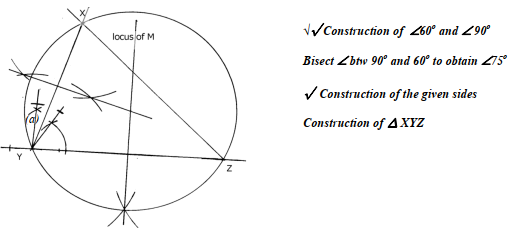
- Using a ruler, a pair of compasses only construct triangle XYZ such that XY = 6cm, YZ = 8cm and ∠XYZ = 75o
- Measure line XZ and ∠XZY
- Draw a circle that passes through X, Y and Z
- A point M moves such that it is always equidistant from Y and Z. construct the locus of M and define the locus
-
- Construct a triangle ABC in which AB=6cm, BC = 7cm and angle ABC = 75o
Measure- Length of AC
- Angle ACB
- Locus of P is such that BP = PC. Construct P
- Construct the locus of Q such that Q is on one side of BC, opposite A and angle BQC = 30o
- Locus of P and locus of Q meet at X. Mark x
- Construct locus R in which angle BRC 120o
- Show the locus S inside triangle ABC such that XS ≥SR
- Construct a triangle ABC in which AB=6cm, BC = 7cm and angle ABC = 75o
- Use a ruler and compasses only for all constructions in this question.
- Construct a triangle ABC in which AB=8cm, and BC=7.5cm and ∠ABC=112½°
- Measure the length of AC
- By shading the unwanted regions show the locus of P within the triangle ABC such that
- AP ≤ BP
- AP >3cm
Mark the required region as P
- Construct a normal from C to meet AB produced at D
- Locate the locus of R in the same diagram such that the area of triangle ARB is ¾ the area of the triangle ABC.
- On a line AB which is 10 cm long and on the same side of the line, use a ruler and a pair of compasses only to construct the following.
- Triangle ABC whose area is 20 cm2 and angle ACB = 90o
- The locus of a point P such that angle APB = 45o.
- Locate the position of P such that triangle APB has a maximum area and calculate this area.
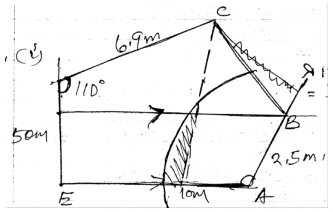
- A garden in the shape of a polygon with vertices A, B, C, D and E. AB = 2.5m, AE = 10m, ED = 5.2M and DC=6.9m. The bearing of B from A is 030º and A is due to east of E while D is due north of E, angle EDC = 110º,
- Using a scale of 1cm to represent 1m construct an accurate plan of the garden
- A foundation is to be placed near to CD than CB and no more than 6m from A,
- Construct the locus of points equidistant from CB and CD.
- Construct the locus of points 6m from A
- shade and label R ,the region within which the foundation could be placed in the garden
- Construct the locus of points in the garden 3.4m from AE.
- Is it possible for the foundation to be 3.4m from AE and in the region?
-
- Using a ruler and compasses only construct triangle PQR in which QR= 5cm, PR = 7cm and angle PRQ = 135°
- Determine ∠ PQR
- At P drop a perpendicular to meet QR produced at T
- Measure PT
- Locate a point A on TP produced such that the area of triangle AQR is equal to one and – a - half times the area of triangle PQR
- Complete triangle AQR and measure angle AQR
- Use ruler and a pair of compasses only in this question.
- Construct triangle ABC in which AB = 7 cm, BC = 8 cm and ∠ABC = 60o.
- Measure
- side AC
- ∠ ACB
- Construct a circle passing through the three points A, B and C. Measure the radius
- Construct ∆ PBC such that P is on the same side of BC as point A and ∠ PCB = ½ ∠ ACB, ∠ BPC = ∠ BAC measure ∠ PBC.
- Without using a set square or a protractor:-
- Construct triangle ABC in which BC is 6.7cm, angle ABC is 60o and ∠BAC is 90o.
- Mark point D on line BA produced such that line AD =3.5cm
- Construct:-
- A circle that touches lines AC and AD
- A tangent to this circle parallel to line AD
- Use a pair of compasses and ruler only in this question;
- Draw acute angled triangle ABC in which angle CAB = 37½o, AB = 8cm and CB = 5.4cm. Measure the length of side AC (hint 37½o = ½ x 75o)
- On the triangle ABC above:
- On the same side of AC as B, draw the locus of a point X so that angle AXC = 52½o
- Also draw the locus of another point Y, which is 6.8cm away from AC and on the same side as X
- Show by shading the region P outside the triangle such that angle APC ≥52 ½o and P is not less than 6.8cm away from AC
Answers
-
- XYZ = 42o + 1o
XZ = 8.8 + 0.1 cm - Bisecting any two sides
Drawing the circle - Perpendicular bisector of YZ
Identification of locus of M
- AC = 8 cm ±0.1
∠ACB = 460 ±10 - AC = 12.9 ±0.1cm
- Line and well shaded B2
- h = 7 ±0.1
- ΔABC _____ Area = ½ x 8 x 7cm
= 28cm
i.e. ¾ x 28 = Area for ARB
= 21cm
i.e. ½ x 8 x h = 21
h = 5.25
-
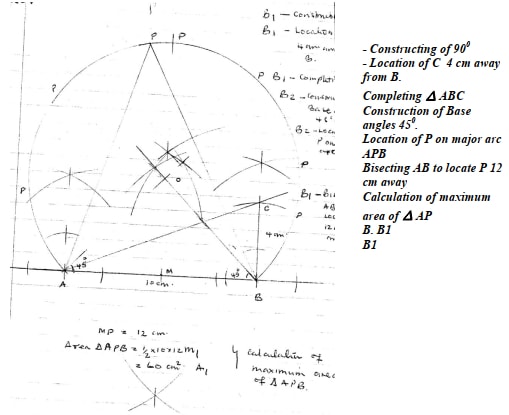
MP = 12 cm
Area ∆ APB = ½ x 10 x 12 = 60 cm2 -
-
- Yes
-
-
-
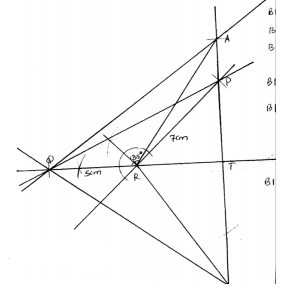
- ∠ PQR = 26° + 1°
- 4.9 ± 0.1cm
- AT = u = 8.7cm
- ∠AQR = 37 ± 1
-
-
- AB = 7 cm, BC = 8 cm
∡ ABC = 60o - AC = 7.6 + 0.1 cm
∡ ABC = 53o ±0.1 - Perpendicular bisectors of any two sides.
Circle drawn
Radius = 4.4.±0.1. cm - ∡ ACB bisected
Bisection line drawn to cut circle at P
∡BPC = ∡BAC = 67o
∡ PBC = 88 ± 0.1o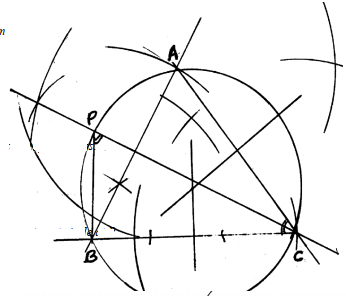
- AB = 7 cm, BC = 8 cm
- B1 – Line AC
B1 Line AB
B1 AD
B3 – Drawing correct circle
B2- Tangent correctly drawn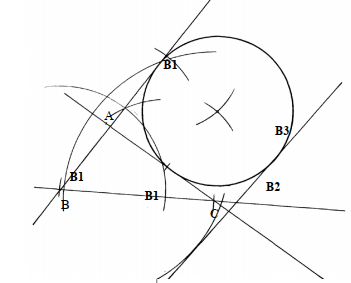
-
- B1 for constructing 150o
B1 for constructing 75oB1 for completing triangle ABC
B1 for AC = 8.8 ± 0.1 - B1 For locating locus centre
B1 for locus of X - B1 for constructing arcs 6.8cm from AC
B1 for locus Y
- B1 For locating locus centre
- B2 for shading the locus of P
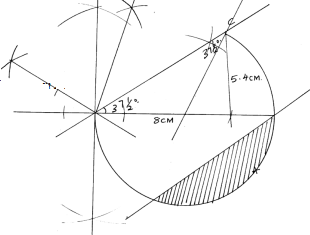
- B1 for constructing 150o
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Loci Questions and Answers - Form 4 Topical Mathematics.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students