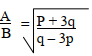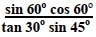Questions
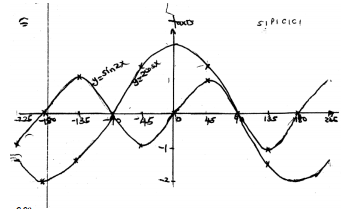
- The table below gives some values of y = sin 2x and y = 2 cox is the range given.
- Complete
xo -225 -180 -135 -90 -45 0 45 90 135 180 225 y - sin 2x3 -1.0 1.0 0 -1.0 1.0 y=2cos x3 -1.4 -1.4 2.0 -1.4 -1.4 - On the same axes, draw the graphs of y = sin 2x and y = 2 cos x.
- Use your graph to find in values of x for which sin 2x – 2 cos x = 0.
- From your graph
- Find the highest point of graph y = sin 2x.
- The lowest point of graph y = 2 cos x.
- Complete
-
- Copy and complete the table below for y =2sin (x +15)o and y =cos(2x -30)o for 0o ≤x ≤360o
x 0 30 60 90 120 150 180 210 240 270 300 y=2sin(x+15) y=cos(2x-30) - On the same axis draw the graphs:
y = 2sin (x + 15) and y = cos(2x -30) for 0o ≤x ≤360o - Use your graph to:
- State the amplitudes of the functions y = 2sin (x +15) and y= cos (2x - 30)
- Solve the equation 2sin (x+15) – cos (2x - 30) = 0
- Copy and complete the table below for y =2sin (x +15)o and y =cos(2x -30)o for 0o ≤x ≤360o
- The diagram below shows a frustum of a square based pyramid. The base ABCD is a square of side 10cm. The top A1B1C1D1 is a square of side 4cm and each of the slant edges of the frustum is 5cm
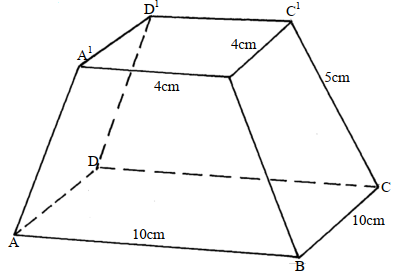
Determine the:- Altitude of the frustrum
- Angle between AC1 and the base ABCD
- Calculate the volume of the frustrum
-
- Compete the table below:
y = 3sin (2x + 15)o
x -180 -150 -120 -90 -60 -30 0 30 60 90 120 y 0.8 -0.8 21 - Use the table to draw the curve y = 3sin (2x +15) for the values – 180o≤ θ ≤120o
- Use the graph to find:
- The amplitude
- The period
- The solution to the equation:-
Sin (2x + 15)o = 1/3
- Compete the table below:
- Make q the subject of the formula in
-
- Complete the table below for the functions y = cos (2x + 45)o and y = -sin (x + 30o)for
- 180o ≤ x ≤ 180o.
-180 -150 -120 -90 -60 -30 0 30 60 90 120 150 180 y=cos(2x+45o) 0.71 -0.97 -0.71 0.71 -0.97 0.97 y=-sin(x+30o) 0.5 0.87 0.5 -0.87 -0.87 0.5 - On the same axis, draw the graphs of y = cos (2x + 45)o and y = -sin (x + 30)o
- Use the graphs drawn in (b) above to solve the equation.
Cos (2x + 45)o + sin(x + 30)o = 0
- Complete the table below for the functions y = cos (2x + 45)o and y = -sin (x + 30o)for
- Without using tables or calculators evaluate
leaving your answer in surd form. -
- Complete the table below for the functions y = 3 sin x and y = 2 cos x
X 0 30 60 90 120 150 180 210 240 270 300 330 360 3sin x 2.6 0 -1.5 -2.6 -3 -1.5 2cos x 1.7 1.0 -1.7 -2 -1.0 1.0 1.7 2 - Using a scale of 2cm to represent 1 unit on the y- axis and 1cm to present 30o on the x-axis ,draw the graphs of y =3sinx and y = 2cosx on the same axes on the grid provided
- From your graphs:
- State the amplitude of y = 3sin x
- Find the values of x for which 3sin x – 2cos x = 0
- Find the range of values of x for which 3sin x ≥2cos x
- Complete the table below for the functions y = 3 sin x and y = 2 cos x
-
- Fill in the following table of the given function:-
x 0 90 180 270 360 450 540 630 720 810 sin½x 0 0.71 0 3sin(½x+60) -2.6 2.6 - On the grid provided draw the graph of the function y = sin ½x and y = 3Sin(½x + 60) on the same set of axes
- What transformation would map the function y = sin ½ x onto y = 3 Sin (½ x + 60)
- State the period and amplitude of function : y = 3 Sin (½x + 60
- Use your graph to solve the equation: 3Sin ( ½x + 60) – Sin ½x = 0
- Fill in the following table of the given function:-
-
- Complete the table below giving your answer to 2 decimal places
xº 0o 30o 60o 90o 120o 150o 180o 2sinxo 0 1 2 1 - cos xo 0.5 1 2 - On the grid provided, using the same axis and scale draw the graphs of :-
y = 2sinxº, and y =1-cosx for
0º≤ x ≤ 180º , take the scale of
2cm for 30º on the x-axis
2cm for 1 unit on the y-axis - use the graph in (b)above too solve the equation 2sinx + cosxº = 1 and determine the range of values of for which 2 sinxº =1-cosxº
- Complete the table below giving your answer to 2 decimal places
- Solve the equation 2 sin (x + 30) = 1 for 0 ≤ x ≤ 360.
-
- Complete the table below, giving your values correct to 1 decimal place
x 0o 10o 20o 30o 40o 50o 60o 70o 80o 90o 100o 110o 120o 130o 140o 150o 160o 170o 180o 10sinx 0 3.4 5.0 7.7 9.4 9.8 10 9.8 9.4 7.7 5.0 3.4 0 - Draw a graph of y = 10 sin x for values of x from 0o to 180o.
Take the scale 2cm represents 20o on the x-axis and 1cm represents 1 unit on the y axis - By drawing a suitable straight line on the same axis, solve the equation: -
500 sin x = -x + 250
- Complete the table below, giving your values correct to 1 decimal place
- Complete the table below for the functions y = cosx and y =2 cos (x 300) for θ≤x ≤ 360o
x 0o 30o 60o 90o 120o 150o 180o 210o 240o 270o 300o 330o 360o Cos x 1 0.87 0.5 -0.5 -0.87 -1.0 0.5 0 0.87 1 2cos 1.73 0 -1.0 -2.0 -1.73 -1.0 1 1.73 2.00 1.73 - On the same axis, draw the graphs of y cos x and y 2cos(x - 30) for O<x < 360°.
- State the amplitude of the graph y = cos xo.
- State the period of the graph y = 2 cos (x + 30°).
- Use your graph to solve
Cos x = 2cos(x+30°)
- Solve the equation sin(2θ+10) = -0.5 for 0 ≤ θ≤ 2πc
- Solve the equation
4 sin 2x = 5 – 4 cos2x for 0° ≤ x ≤ 360° -
- Complete the table given below by filling in the blank spaces
X 0 15 30 45 60 75 90 105 120 135 150 165 870 4cos 2x 4.00 2.00 0 -2.00 -3.46 -4.00 -3.46 -2.00 0 2.00 4.00 2 sin(2x+30o) 1.00 1.73 2.00 1.73 0 -1.00 -1.73 -2.00 0 -1.73 0 1.00 - On the grid provided; draw on the same axes, the graphs of y = 4cos 2x and y =2sin(2x +30o) for 0o≤X ≤180o. Take the scale: 1cm for 15o on the x-axis and 2cm for 1unit on the y-axis
- From your graph:-
- State the amplitude of y = cos 2x
- Find the period of y = 2sin (2x + 30o)
- Use your graph to solve:-
4cos2x – 2sin (2x +30) = 0
- Complete the table given below by filling in the blank spaces
Answers
-
-
Xo -225 -180 -135 -90 -45 0 45 90 135 180 225 y=sin2x 0 0 1.0 1.0 0 0 y=2cosx -2.0 0 1.4 1.4 0 -2.0 -
- -90o or 90o
- Highest point 1 unit
- Lowest point - 1.4
-
-
-
x 0 30 60 90 120 150 180 210 2sin(x+15o) 0.52 1.41 1.93 1.93 1.41 0.52 -0.52 -
1.41Cos(2x -30o) 0.87 0.87 0 -0.87 0.87 0 0.87 0.87 -
x 240 270 300 330 360 2sin(x+15o) -1.93 -1.93 -1.41 -0.52 0.52 Cos (2x -30o) 0 -0.87 -0.87 0 0.87 - Amplitudes:, y = 2 sin ( x + 15)
= 2units
y = cos (2x – 30)
=1unit
12o, 159o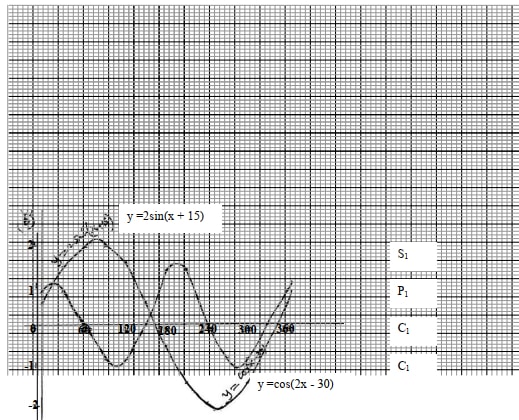
- Amplitudes:, y = 2 sin ( x + 15)
-
- Determine the
- Altitude of the frustrum
Solution
A1C1 = √ 42 + 42 = √32
AC = √102 + 102
= √200
= 10√2
AM + XM = 10√2 - 4√2
= 6√2
AM = 6√2/2 = 3√2
Height = AM =√52 – (3√2)2 = √25 – 18
= √7 = 2.646
∴ the altitude of the frustrum = 2.646 cm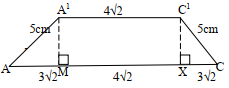
- Angle between AC and the base ABCD
AX = 3√2 + 4√2 = 7√2
Tan ø = CX/AX =√7/7√2 = 2.646/9.898
= 0.2673
θ = tan-1 0.2673
= 14.96°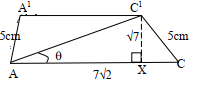
- Volume of pyramid = 1/3 bh
AC = 10√2
A1C1= 4√2
L.S.F = 10:4
∴ h + 2.646 = 10
h 4
4(h + 2.646) = 10h
4h + 10.584 = 10h
6h = 10.584
h = 1.764
H = h + 2.646
= 1.764 + 2.646 = 4.410
Vf = (1/3 x 10 x 10 x 4.41) – (1/3 x 4 x 4 x 1.76)
=441.0/3 - 28.224/3
=413.776/3
= 137.592cm3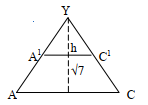
- Altitude of the frustrum
- table completed
-
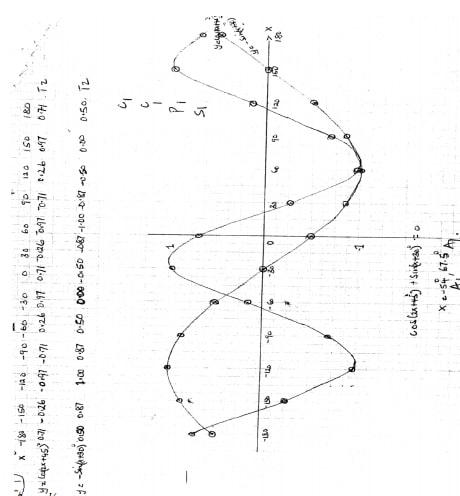
- 3 P1 – plotting
S1- scale
C1 – smooth curve - 180o
- Line y = 1 drawn
x = 4.5o or 72.8o – 107.2o - 175.4o
- 3 P1 – plotting
- (A/B)2 = p + 33q
q – 3P
A2q – 3A2P = BP + 3Bq
Aq2 – 3Bq = BP + 3A2P
2(A2 – 3B) = BP + 3A2P
Q = BP + 3A2P
A2 – 3B -
- √3x ½
2
1 x 1
√3 √2
√3 x √6
4 1
√18
4
3 √2
4 -
-
x 0 30 60 90 120 150 180 210 240 270 300 330 360 3sinx 1.5 2.6 1.5 -2.6 0 2cosx 2 0 -1.0 -1.7 0 -
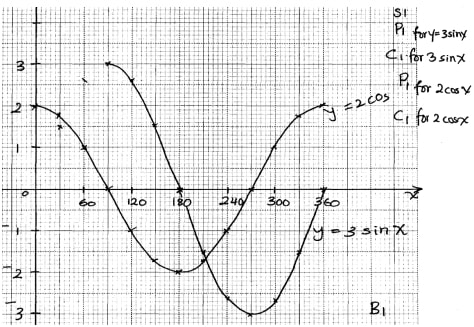
- Amplitude =3
- x = 36o
x = 216o - 33o ≤x ≤213o
-
-
x 0 90 180 270 360 450 540 630 720 810 sin ½x 0 0.71 1 0.71 0 -0.71 -1 -0.71 0 0.71 3Sin (½x + 60) 2.6 2.9 1.5 -0.78 -2.6 2.9 -1.5 0.78 2.6 2.9 -
x 0o 30o 60o 90o 120o 150o 180o 2 sin x 0 1 1.73 2 1.73 1.00 0 1-Cos x 1 0.13 0.50 1 0.06 1.87 2 
- Sin (x + 30) = 0.5
x + 30 = 30o
x = 0
0, 180, 360 -
- 10sin x = -1/50 + 5
Y = -1/50 + 5
X1 = 28o ±1X 0 50 y 5 4
X2 = 70o ±1
-
-
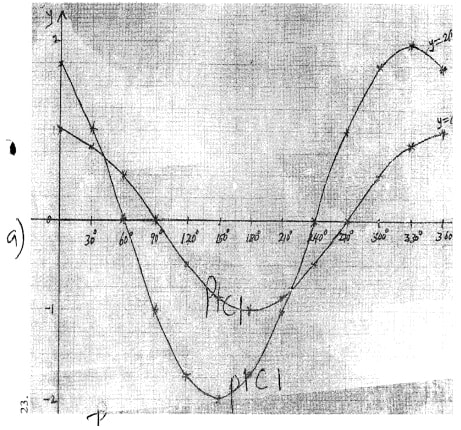
- amplitude = 1
- Period = 360°
- 45°, 219°
-
- 2θ+ 10 = 210o, 330o, 570o, 690o
2θ= 200, 320, 560, 680
= 100o, 160o, 280o, 340o
= 5πc , 8πc, 14πc, 17πc
90 9 9 9 - 4sin 2x+4cos x-5 = 0
4(1-cos2x) + 4 cosx - 5= 0
4cos2x – 4 cosx + 1=0
4cos2x – 2cosx – 2cos x +1 =0
(2cos x – 1)2 = 0
X = 60°, 300° -
-
x 15o 60o 150o 165o 4cos2x 3.46 3.46 2sin(2x+30o) 1.00 -1.00 - graph
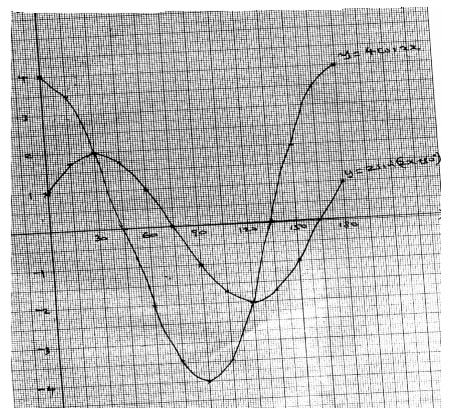
- Amplitude = 4
- period = 180o
- x = 30o, 120o
-
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Trigonometric Ratios 3 Questions and Answers - Form 4 Topical Mathematics.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students