Questions
- A particle moves such that t seconds after passing a given point O, its distance S metres from O is given by S= t (t-2) (t-1)
- Find its velocity when t = 2 seconds
- Find its minimum velocity
- Find the time when the particle is momentarily at rest
- Find its acceleration when t = 3 seconds
- The table below gives the values of x and y for the curve y=x2 +1
X 0 1 2 3 4 5 6 7 8 9 10 y 1 2 10 17 37 50 82 - Complete the table
- Use the mid- ordinate rule to estimate the area enclosed by the curve y = x2 + 1. Use five coordinates
- Using integration, calculate the actual area in (a) above
- Calculate the percentage error in the estimated area
- The gradient function of a curve is given by the expression 2x + 1. If the curve passes through the point (-4, 6); find the equation of the curve
- A particle P moves in a straight line so that its velocity, V m/s at time t seconds where t ≥0 is given by v = 28 + t – 2t2
Find;- the time when P is instantaneously at rest
- the speed of P at the instant when the acceleration of P is zero
- Find the acceleration of P when the article is instantaneously at rest
- Find the distance covered by the particle during the 3rd second, when at t = 0 D = 5M
- A particle K moves a long a straight line 50 cm long. At time t = 0, k is at A and t seconds later its velocity vcm/s is given by v = 15 + 4t – 3t2.
- Write down the expression for;
- The acceleration of K at time t seconds.
- The distance of K from A at time t seconds.
- Find t when K is instantaneously at rest.
- How far is K from A at this time?
- Find the period of time during which the acceleration of P is positive.
- Write down the expression for;
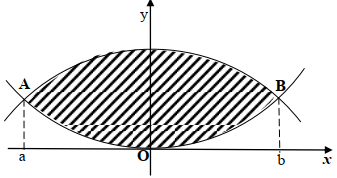
- The diagram below shows the sketch of the curve y = x2 and y = -x2 + 8 intersecting at A and B:-
- Find the value of a and b hence find the coordinates of A and B
- Find the area enclosed by x = a, x = b, the axis and:-
- the curve y = x2
- the curve y = -x + 8
- The distance from a fixed point of a particle in motion at any time t seconds is given by :- S = t3– 5/2t2 + 2t + 5 metres.
Find its:- Acceleration after t seconds
- Velocity when acceleration is zero
- A particle moves in a straight line. It passes through point O at t = 0 with a velocity v = 5 m/s. The acceleration a m/s2 of the particle at time t seconds after passing through O is given by a = 6t + 4
- Express the velocity v of the particle at time t seconds in terms of t.
- Calculate the velocity of the particle when t = 4.
- Express the displacement s by the particle after t seconds in terms of t.
- Calculate the distance covered by the particle between t = 1 and t = 4.
- The displacement S metres of a particle moving along a straight line after t seconds is given by. S = 3t + 3t2/2 – 2t3
- Find its initial acceleration
- Calculate:
- The time when the particle was momentarily at rest
- Its displacement by the time it came to rest momentarily
- Calculate the maximum speed attained
- Find the equation to the tangent to the curve:- y = 4x3 – 2x2 – 3x + 5 at the point (2, 23)
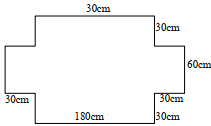
- A farmer wanted to make a trough for cows to drink water. He had a metal sheet measuring 240cm by 120cm and 1cm thick. The density of the metal is 2.5g/cm3. A square of sides 30cm is removed from each corner of the rectangle and the remaining part folded to form an open cuboid.
- Sketch the sheet after removing the squares for the four corners, showing all the dimensions
- Calculate:-
- The area of the metal which forms the cuboid
- The mass of the empty cuboid in Kilograms
- The cuboid is filled with water whose density is 1g/cm3. Calculate the mass of the cuboid when full of water
- A rectangular sheet of cardboard is 8cm long and 5cm wide. Equal squares are cut away at each corner and the remainder is folded so as to form an open box. Find the maximum volume
- Find the equation of the normal to the curve :- y = x3 – 2x – 1 at ( 1, -2)
- Determine the nature of the turning points to the curve y = x3 – 3x + 2; Hence in the space provided below, sketch the curve
- A particle moves in a straight line so that its velocity, v/m/s at time t seconds where t 0 is given by v = 28 + t – 2t2
Find:-- The time when P is instantaneously at rest
- The speed of P at the instant when the acceleration of P is zero
- Given that P passes through the point O of the line when t = 0; Find the distance of P from O when P is instantaneously at rest
- A particle moves in a straight line from a fixed point. Its velocity V m/s after t seconds is given by V = 9t2 −6t + 2. Calculate the distance traveled by the particle during the 2nd second. (4 mks)
Answers
- S = t3 – 3t2 + 2t
- V = ds = 3t2 – 6t + 2
dt
When t = 2
V = 3(4) – 6(2) + 2
= 2m/s - At minimum velocity :
dv = 0
dt
dv = 6t – 6
dt
6t – 6 = 0
t = 1
Min-velocity = 3(1)2 – 6(1) + 2
= -1m/s - 3t2 – 6t + 2 = 0
t = 6± √[(-6) – 4 (3)(2)]
6
= 6 ±5.2
6
t = 1.58 or 0.4sec - acc = dv = 6t − 6
dt
a = 6(3) – 6= 12m/s2
- V = ds = 3t2 – 6t + 2
-
-
X 2 5 8 10 y 5 26 65 101 - A = h(2 + 10 + 26 + 50 + 82)
= 2 x 170
= 34 square units - A = (x2 + 1 ) dx
= (1000/3 + 10) – 0
= 333.33 + 10
= 343.33
= 343.33 square units - Percentage error = 3.33/343.33 x 100 %
= 0.97%
-
- y = 2x2 + x + c
2
a + x = -4 , y = 6
6 = (-4)2 – 4+c
c = -6
y = x2+ x - 6 -
- -2t2 + t + 28 = 0
P = -56
S = 8, -7
-2t2 + 8t – 7t + 28 = 0
-2t(t – 4) – 7(t – 4) = 0
t = 3.5
t = 4 - AC = -4t + 1
- 4t + 1 = 0
T = ¼
V = -2(¼)2 + ¼ + 28
V = 28.125 - Acc = - 4t + 1
At rest t = 3.5, t = 4
Acc = -4 x 4 + 1
= -15m/s2
At t = 3.5
A = -13m/s2 -
- D= 2t3 + t2 + 28t + 5
3 2
Distance = -2 x 33/3 + 32/3 + 28 x 3 + 5 = 75.5m - D = 2t3 + t2 + 28t + 5
3 2
D = -2 x 33/3 + 32/3 + 28 x 3 + 5
= -18 + 4.5 + 84 + 5
= 70.5 + 5 = 75.5
- D= 2t3 + t2 + 28t + 5
- -2t2 + t + 28 = 0
-
- V = 15 + 4t – 3t2
dv = Acc = 4 – 6t
dt - V = 15 + 4t – 3t2
V = dv = 15 + 4t – 3t2
dt
∴ S = (15 + 4t – 3t2) dt
S = 15t + 4t2 - 3t2 + C
2 3
S = 15t + 2t2 – t3 + C
- V = 15 + 4t – 3t2
- Acc = 0 hence dv = 0
dt
4 – 6t = 0
-6 = -4
t = 2/3 sec. - S = 15t + 2t2 – t3 + C
= 15(2/3) + 2(2/3)2 − (2/3)3
= 10 + 8 = 8
1 9 27
= 286
27 = 10.5925 ≃ 10.59
- Acc = 0 hence dv = 0
- Acc. 4 – 6t
-4 = -6t
t = 2/3 Acc.= 0
∴ Time is 0 and 2/3
Bth. 0 and 2/3 sec.
-
- x2 = -x2 + 8
2x2 = 8
x = 2 a = -2, b = 2 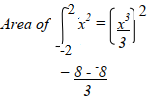
- Area = 80 + 16 = 96
3 3 3
= 32
- x2 = -x2 + 8
- a = d2s = d2 (t3 -5t2 + 2t + 5)
dt2 dt2 2
= d =3t2 – 5t + 2
dt
= 6t -5
If a = 0
6t – 5 = 0
t = 5/6
v = ds = 3t2 – 5t2 = 3 x 25 – 5 x 5 + 2
dt 36 6
= -1 m/s
12 -
- V = 6t + 4 = 3t2 + 4t + c
5 = 3(0)2 + 4(0) + c
5 = c
V = 3t2 + 4t + 5 - V = 3(4)2 + 4 (4) + 5
= 69 m/s -
- ∫3t2 + 4t + 5
= t3 + 2t2 + 5t + c
When t = 0 S = 0
S = t3 + 2t2 + 5t - S = t3 + 2t2 + 5t
= (4)3 + 2(4)2 + 5(4) - (1)3 + 2(1)3 + 5(1)
= 108 m
- ∫3t2 + 4t + 5
- V = 6t + 4 = 3t2 + 4t + c
-
- S = 3t + 3t2 – 2t3
2
ds = v = 3 + 3t – 6t2
dt
dv = a = 3 – 12t t = 0
dt
a = 3m/s2 - O = -6t2 = 3t + 3
t = 1 - S = 3(1) + 3(1)2 – 6(1)3
2
= 3 + 3/2 – 2
=2/2 + 3/2 = 5/2
- O = -6t2 = 3t + 3
- V = 3 + 3(1) -6 (1)
= 3+3 – 6
= 0m/s
- S = 3t + 3t2 – 2t3
- dy/dx = 12x2 – 4x – 3 at (2,23)
= 12(4) – 4(2) – 3
= 48 – 8 – 3
= 40 – 3
= 37
M = y –y or y = mx + c
= 23 – y
2 – x
23 – y = 37(2 - x)
23 – y = 74 - x
23 = 37 (2) +c
C = 23 – 74 = -51
Hence equation is y = 37x – 5 -
- (180 x 30 x 2) = 10800
(60 x 30 x 2 ) = 3600
(180 x 60 x 1 = 10800
Total area = 25200cm2 - Volume of the cuboid
= (180 x 60 x 30) cm3= 324,000cm3
Mass = (2.5 x 180 x 60x 30)
= 810000g
1000
= 810kg
Volume of water = (324,000cm3)
Mass of water = (324,000 x 1)
1000
= 324kg
Mass of cuboid = 324 + 810
Full of water = 1,134kg
- (180 x 30 x 2) = 10800
- Let length of square cut off be x
Length of box = 8 – 2x
Width of box = 5 – 2x
Height of box = x
V = (8 -2x) (5-2x)x
= 4x3 – 26x2 + 40x
dv = 12x2 – 52x + 40
dx
12x2 – 52 x + 40 = 0
3x2 – 13x + 10 = 0
3x2 – 10x – 3x + 10 = 0
X(3x -10) – 1 (3x-10) = 0
(x -1) (3x -10) = 0
x = 1 x = 10/3
d2= 24x – 52
dx2
x = 1
d2= 24x – 52 = -28
dx2
maximum
x = 1cm gives maximum vol
(8-2) (5-2) X 1 = 6 x 3
= 18cm3 -
- dy = 3x2 – 2
dx
Gradient of the tangent is 1 so, gradient of the normal is -1
y –-2 = -1
x -1 1
y + 2 = -1
x– 1 1
y = -x -1 - dy = 3x2 – 3 = 0
3(x2 -1) = 0
(x-1) =0
x =1, y = 0 & x = -1, y = 4
Coordinates of turning points
(1,0) and (-1, 4)
For (1,0) x<1 , dy is –ve
dx
x > 1, dy is +ve
dx
(1,0) is a minimum point for (-1, 4) x < -1, dy is +ve
dx
(1, 0) is a minimum point for (-1, 4) x < -1, dy is +ve
dx
x > -1, dy is –ve
dx
⇒ (-1, 4) is a maximum point
To sketch the curve we need
(i)Its turning points and their nature
(ii)The points the graph cuts the x and y axis i.e the x and y-intercepts - ⇒Indicating that the curve turns at (-1, 4) (1, 0) and cuts the y-axis at (0, 2) B1
⇒C1 for correct sketch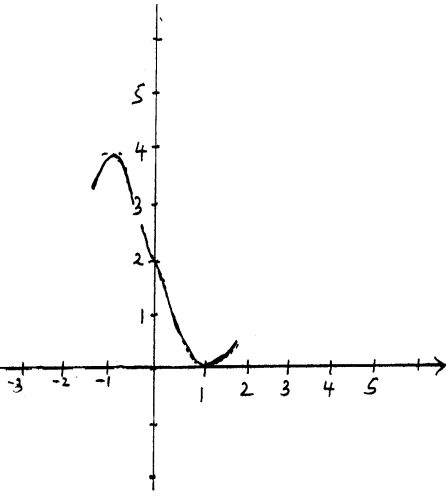
- dy = 3x2 – 2
-
- -2t2 + t + 28 = 0
t2– t – 28 = 0
2t2 – 8t) + (7t – 28) = 0
2t(t - 4) +7(t-4) = 0
(2t + 7) (t-4) = 0
t = -3.5 or 4
p.B at rest at t= 4seconds - a = 1-4t
1 – 4t = 0
0.25s = t
V = 28 + 25 – 2 (0.25)2
= 28.25 – 0.125
V = 28.125m/s - S = 28t + t2 – 2t3 + C
2 3
when t = 0, s = 0
∴S = 28t + t2 – 2t
PB at rest after 4s
∴S = 28 x 4 x 42 – 2 x 43
3
= 112 + 8 – 42.667
= 120 – 42.6667= 77.33m
- S = 28t + t2 – 2t3 + C
- -2t2 + t + 28 = 0
Join our whatsapp group for latest updates
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Download Differentiation Questions and Answers - Form 4 Topical Mathematics.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students