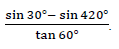SECTION I (50 marks)
Answer all questions from this section in the spaces provided.
- The roots of the quadratic equation x2+px=q are x= −3/7 and x=2. Find the values of p and q. (3mks)
- Without using a mathematical table or a calculator, evaluate leaving your answer in the form. a√b+c., where a, b and c are constants. (3mks)
- Two matrices P and Q are such that
. Given that the determinant of QP is 44, find the value of k. (3mks)
- Find the value of x given that log(x−1)+2= log(3x+2)+ log25. (3mks)
- The equation of a circle is given as x2+ y2+4x−2y−4=0. Determine the centre and the diameter of the circle. (3mks)
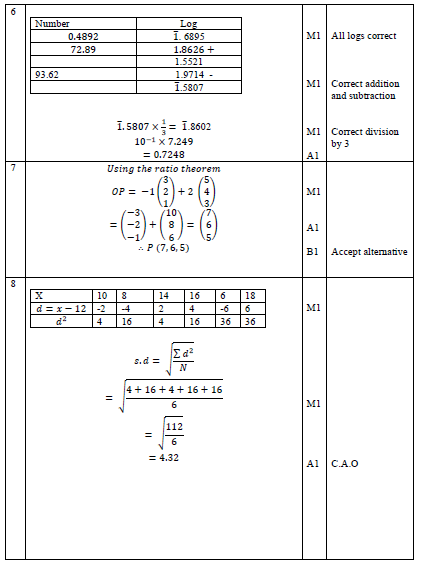
- Using logarithms, evaluate
(4mks)
- If
. P divides AB externally in the ratio 2:1. Find the coordinates of P. (3mks)
- Kapsabet Boys’ handball team scored the following goals in 6 matches; 10, 8, 14, 16, 6 and 18. Using assumed mean of 12, determine the standard deviation leaving your answer to 2 d.p. (3mks)
- The gradient of a curve at point (x,y) is 4x−6. The curve has a minimum value at 51/2. Find the equation of the curve. (3mks)
- The nth term of G.P is given by 5 x 2n-2
- Write down the first 4 terms of the G.P (1mark)
- Calculate the sum of the first 6 terms. (2marks)
-
- Expand (1− 1/2x)5 in ascending powers of x leaving the coefficients as fractions in their simplest form. (2mks)
- Using the first three terms in the expansion in (a) above, estimate the value of (19/20)5 (2mks)
- A 2– digit number is made by combining any two of the digits 1, 3, 5, 7, 9 at random
- Write down all the possible outcomes. (1mk)
- Find the probability that the number is prime. (1mk)
- Find the percentage error in evaluating (a+b)−c, if a=3.2 cm,b=5cm and c=2.0cm, leaving your answer to the nearest 4 s.f (3mks)
- Three quantities A, B and C are such that A varies directly as B and inversely as the square root of C. Find the percentage decrease in A if B decreases by 5.2% and C increases by 44%. (3mks)
- Write r in terms of u, y, p and t (3mks)
- Using the diagram below, find the angle;
- Plane BFC makes with ABCD (2mks)
- Plane ABFE makes with ABCD (2mks)
SECTION II (50 marks)
Answer only five questions from the section in the spaces provided.
- The table below shows monthly income tax rates for a certain year.
Monthly taxable income in Ksh. Tax rate (%) in each shilling 0 – 11180 10 11181 – 21714 15 21715 – 32248 20 32249 – 42782 25 Above 42782 30
Mr Tundu earned a salary of Ksh 58 000, a house allowance of Ksh. 8 200 and a commuter allowance of Ksh. 6 000. He gets a monthly personal relief of Ksh. 1280.- Calculate
- Mr Tundu’s monthly taxable income in Ksh. (2mks)
- The tax payable by Mr Tundu in that month. (5mks)
- The following month that year, Tundu’s basic salary was raised by 5%. Determine his net salary for that month. (3mks)
- Calculate
-
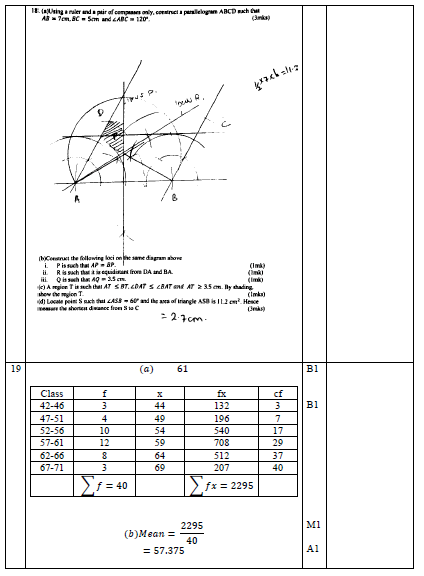
- Using a ruler and a pair of compasses only, construct a parallelogram ABCD such that AB=7cm,BC=5cm and ∠ABC=120°. (3mks)
- Construct the following loci on the same diagram above
- P is such that AB=BP. (1mk)
- R is such that it is equidistant from DA and BA. (1mk)
- Q is such that AQ=3.5 cm. (1mk)
- A region T is such that AT ≤BT,∠DAT ≤ ∠BAT and AT ≥3.5 ??. By shading, show the region T. (1mks)
- Locate point S such that ∠ASB=60° and the area of triangle ASB is 11.2 cm2. Hence measure the shortest distance from S to C (3mks)
- The marks scored by 40 students in a mathematics class were shown in the table below:
Marks 42 - 46 47 - 51 52 - 56 57 - 61 62 - 66 67 - 71 Number of students 3 4 10 12 8 3 - State the upper class limit of the modal class (1mks)
- Estimate the mean mark (3mks)
- If the pass mark is 55%, how many students passed? (3mks)
- Find the range of marks scored by the middle 50% of the students. (3mks)
- A plane leaves an airport X (41.5° N,36.4° W) at 9.00 a.m. and flies due North to airport Y on latitude 53.2° N.
- Calculate the distance covered by the plane in km. (3mks)
- After stopping for 30 minutes to refuel at Y, the plane then flies due East to airport Z, 2500 km from Y. Find the:
- Position of Z (3mks)
- Time the plane lands at Z, if its speed is 500km/h. (4mks)
(take Π= 22/7 and the radius of the earth R=6370 km)
-
- Complete the table below to 2 dp. (2mks)
?° 0 30 60 90 120 150 180 210 240 270 sin(?+30°) 0.50 0 -0.50 0.87 2cos(?+30°) 1.73 0 -1.73 - On the same axes, draw the graphs of y= sin(x+30°) and y=2cos(x+30°). (5mks)
- State the amplitude and period of each wave. (2mks)
- Use the graph to solve the equation 2cos(x+30°)= sin(x+30°). (1mk)
- Complete the table below to 2 dp. (2mks)
- Triangle OPQ is such that OP=p and OQ=q. Point R divides OP in the ratio 1:3 and point S divides PQ in the ratio 5:2. OS and RQ meet at T.
- Express OS and QR in terms of p and q. (3 mks)
- Given that OT=kOS, express OT in terms of k, p and q. (1mk)
-
- Given also that RT=hRQ, express OT in terms of h, p and q. (2mks)
- Find the values of h and k. (3mks)
- In what ratio does O divide TS? (1mk)
- Using the equation of the curve y= 1/2x2−2 for 0≤x≤8
- Complete the table below. (1mks)
x 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 y - Using trapezium rule with 8 strips, determine the area bounded by the curve, the lines x=0,x=8 and the x-axis. (2mks)
- Find the area in (b) above using the mid-ordinate rule with 4 strips (2mks)
- Find the exact area by integration (3mks)
- What is the percentage error in using the mid-ordinate rules? (2mks)
- Complete the table below. (1mks)
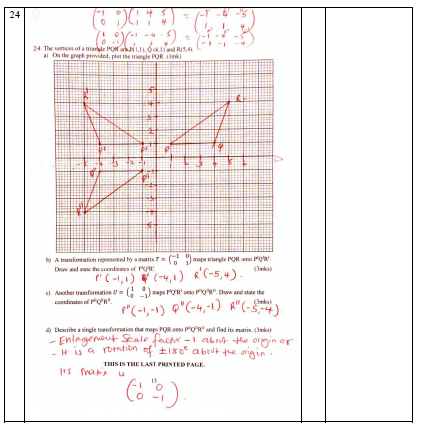
- The vertices of a triangle PQR are P(1,1), Q (4,1) and R(5,4).
- On the graph provided, plot the triangle PQR. (1mk)
- A transformation represented by a matrix T= (−10 01) maps triangle PQR onto PIQIRI. Draw and state the coordinates of PIQIRI. (3mks)
- Another transformation U= ( 10 0−1) maps PIQIRI onto PIIQIIRII. Draw and state the coordinates of PIIQIIRII. (3mks)
- Describe a single transformation that maps PQR onto PIIQIIRII and find its matrix. (3mks)
Download Mathematics Paper 2 Questions and Answers - Kapsabet Mocks 2020/2021.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students