INSTRUCTIONS TO CANDIDATES
- Write your name, index number and class.
- The paper contains two sections: Section I and II
- Answer ALL questions in section I and ONLY FIVE questions from section II.
- All working and answers must be written on the question paper in the spaces provided below each question.
- Marks may be awarded for correct working even if the answer is wrong.
- Negligence and slovenly work will be penalized.
- Non-programmable silent electronic calculators and mathematical tables are allowed for use.
FOR EXAMINER’S USE ONLY
SECTION 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
TOTAL |
SECTION II
|
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
TOTAL |

QUESTIONS
SECTION 1 (50 Marks)
Answer ALL questions from this section
- Evaluate:
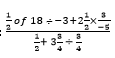 (3 marks)
(3 marks) - The straight line joining the points P (a, 7) and Q (13, a) is parallel to the line whose equation is 3y + 2x = 9. Find the value of a. (3 marks )
- Solve the following inequalities and represent the solution on a number line and hence state the integral values of x
7x – 4 ≤ 9x + 2 < 3x + 14 (4 marks) - The gradient of curve at any point is given by 2x – 1. Given that the curve passes through point (1, 5), find the equation of the curve. (3 Marks)
- Solve for x in the equation. (3 marks)
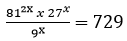
- The GCD of 6480, 7200 and a third number is 144. The L.C.M of the three numbers is 25 x 35 x 52 x 73. Find the smallest third number. (3 marks )
- Mr. Waweru needs to import a car from Japan where cost is USD 5000 outside Kenya. He intends to buy the car through an agent who deals in Japanese yen. The agent will charge him 20% commission on the price of the car and further 80,325 Japanese yen for shipment of the car. How much Kenya shillings will he need to send to the agent to obtain the car given that?
1USD = 105.00 yen and 1USD = KSh. 63.00 (3 marks) - Use tables of reciprocals only to find the value of
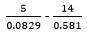 (3 marks)
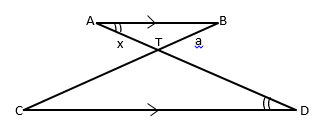
(3 marks) - The figure below AB//CD, AD and BC intersect at T. Given that AT:TD = 1:3 and CB = 12cm. Calculate the length of TB. (3 marks)
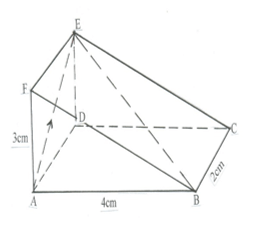
- Draw the net of the solid shown below. (3 marks )
- The figure below shows a histogram. (3mks)
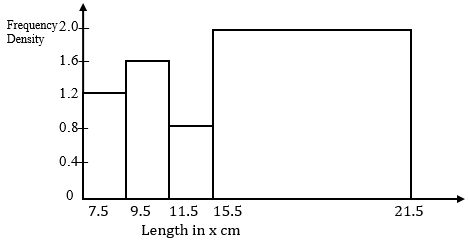
Fill in the table below the missing frequencies.
Length in x cm
Frequency
7.5 ≤ x ≤ 9.5
12
9.5 ≤ x ≤ 11.5
11.5 ≤ x ≤ 15.5
15.5 ≤ x ≤ 21.5
- Solve for x: (log2x )2 - Log2 x3 = 4 (4 marks)
- Mutua bought 8 pairs of trousers and six shirts at Sh. 4160. Had he bought twice as many shirts and half as many trousers, he would have saved Sh. 160. Find the cost of each item. (3 marks)
- Two containers have base area of 750cm2 and 120cm2 respectively. Calculate the volume of the larger container in litres given that the volume of the smaller container is 400cm3. (3 marks)
- In the figure below O is the centre of circle PQRS. ∠PTS = 56º and ∠PQS = 28º and TPQ is a straight line.
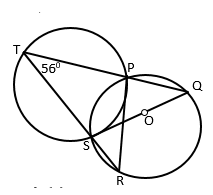
Find:- ∠TSP (2mark)
- ∠PRQ (1 mark)
- Simplify the following expression.
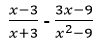 (3 marks)
(3 marks)
SECTION II (50 marks)
- Three partners Mutua, Muthoka and Mwikali contributed Sh. 600,000, Sh. 400,000 and Sh. 800,000 respectively to start a business of a matatu plying Mbumbuni – Machakos route. The matatu carries 14 passengers with each paying Sh. 250. The matatu makes two round trips each day and ever full. Each day Sh. 6000 is used to cover running costs and wages.
- Calculate their net profit per day. (2 marks)
- The matatu works for 25 days per month and is serviced every month at a cost of KSh.10, 000. Calculate their monthly profit in June. (1 mark)
- The three partners agreed to save 40% of the profit, 24% to be shared in the ratio of their contribution. Calculate Muthoka’s share in the month of July (4 marks)
- The matatu developed mechanical problems and they decided to sell it through an agent who charged a commission of 5% on selling price. Each partner received KSh. 475,000 from the agent after he had taken his commission. Determine the price at which the agent sold the matatu. ( 3 marks)
- The income tax rates in a certain year are as shown below.
Omar pays Sh. 4000 as P.A.Y.E per month. He has a monthly house allowance of KSh.10800 and is entitled to a personal relief of KSh. 1,100 per month. Determine:Income (k₤ – p.a
Rate (KSh. per ₤)
1 – 4200
2
4201 – 8000
3
8001 – 12600
5
12601 – 16800
6
16801 and above
7
- his gross tax per annum in Kshs (2 Marks)
- his taxable income in K₤ per annum (2 marks)
- his basic salary in Ksh. per month. (2marks)
- his net salary per month (2 marks)
-
-
- Fill the table below for the function.
y = 2x2 + 5x – 12 for -8 ≤ x ≤ 4 (2 marks)
x
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
2x2
98
18
2
32
5x
-35
-15
5
20
-12
-12
-12
-12
-12
y
51
-9
-5
40
- Using the table, draw the graph of the function y = 2x2 + 5x – 12. Use the scale 1cm to 1 unit on the x-axis and 1cm for 10 units for the y – axis (4 marks)

- Fill the table below for the function.
- Use the graph drawn above to solve the following equations.
- 2x2 + 5x – 12 = 0 (2 marks)
- 3 – 7x – 3x2 = 0 (2 marks)
-
- The diagram below shows the speed-time graph for a bus travelling between two stations. The bus begins from rest and accelerates uniformly for 30 seconds. It then travels at a constant speed for 60 seconds and finally decelerates uniformly for 40 seconds.
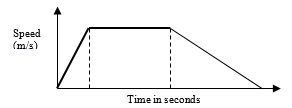
Given that the distance between the two stations in 2090m. Calculate- The maximum speed, in km/h the bus attained (3 Marks)
- The acceleration (2 Marks)
- The distance travelled during the last 20 seconds (2 Marks)
- The time the bus takes to travel the first half of the journey (3 Marks)
- In the figure below, K,L,M and N are points on the circumference of the circle centre O. The points K, O, M and P are on a straight line. PN is tangent to the circle at N. ∠KOL = 130º and ∠MKN = 40º.
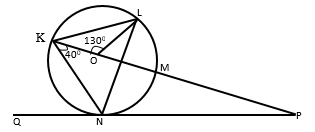
Stating the reason in each case, find the values of the following angles,- MLN (2 marks)
- OLN (2 marks)
- LNP ( 2 marks)
- MPN ( 2 marks)
- KNQ (2 marks)
- The figure below shows a model of a solid in the shape of a frustum of a cone with a hemispherical top.
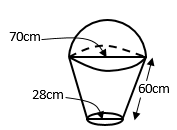
The diameter of the hemispherical top is 70cm and is equal to the diameter of the top of the frustum. The frustum has a base diameter of 28cm and a slant height of 60cm.- Calculate the area of the hemispherical surface. ( 1mark)
- Calculate the slant height of the cone from which the frustum was cut. (4marks)
- Calculate the total surface area of the mode. (5 marks)
- The figure below shows triangle OPQ in which OS = 1/3 OP and OR = 1/3 OQ. T is a point on QS such that QT = 3/4 QS
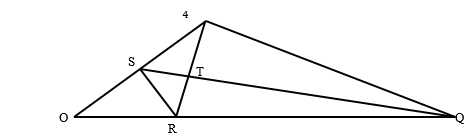
- Given that OP = p and OQ = q, express the following vectors in terms of p and q.
- SR (1 Mark)
- QS (2 Marks)
- PT (2 Marks)
- TR (2 Marks)
- Hence or otherwise show that the points P, T and R are collinear. (3 Marks)
- Given that OP = p and OQ = q, express the following vectors in terms of p and q.
- The displacement S metres of a body moving along a straight line after t seconds is given by
S = -2t3 + 3/2 t2 + 3t- Find its initial acceleration. (3 marks)
- Calculate:-
- The time when the body was momentarily at rest. (3 marks)
- Its displacement by the time it comes to rest momentarily (2 marks)
- Calculate the maximum velocity attained (2 marks)

MARKING SCHEME
SECTION 1 (50 Marks)
Answer ALL questions from this section
- Evaluate:
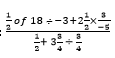 (3 marks)
(3 marks)
Numerator
9 ÷ -3 + 5/2 × 2/-5
-3 - 3/2 = -9/2
Denominator
1/2 + 15/4 × 4/3
=51/2
N = -9 ÷ 11
2 2
= -9 × 2
2 11
= -9
11 - The straight line joining the points P (a, 7) and Q (13, a) is parallel to the line whose equation is 3y + 2x = 9. Find the value of a. (3 marks )
3y = -2x + 9
y = -2/3 x + 3
g=(-2)
3
g=(7-a) =(-2)
(a-13) 3
-2a + 26 = 21 – 3a
a = -5 - Solve the following inequalities and represent the solution on a number line and hence state the integral values of x
7x – 4 ≤ 9x + 2 < 3x + 14 (4 marks)
7x – 4 ≤ 9x + 2 ..(i)
9x + 2 < 3x + 14(ii)
Solving (i)
7x – 4 ≤ 9x + 2
-2x ≤ 6
x ≥ -3
Solving equation (ii)
9x + 2 < 3x + 14
6x < 12
x < 2
Combining (i) and (ii)
-3 ≤ x < 2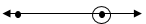
-3 – 2 -1 0 1 2
Integral values are
-3, -2, -1, 0, 1 - The gradient of curve at any point is given by 2x – 1. Given that the curve passes through point (1, 5), find the equation of the curve. (3 Marks)
dy = 2x – 1 y = x2 - x + c
dx
5 = 1 – 1 + c c = 5
y = x2 - x + 5 - Solve for x in the equation. (3 marks)
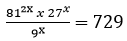
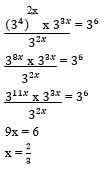
- The GCD of 6480, 7200 and a third number is 144. The L.C.M of the three numbers is 25 x 35 x 52 x 73. Find the smallest third number. (3 marks )
6480 = 24 x 34 x 5
7200 = 25 x 32 x 52
GCD = 24 x 32
LCM = 25 x 35 x 52 x 73
x=(29 x37 x 52 x 73)
(25×34×52 )
Third number: 24 x 33 x 73
= 148,176 - Mr. Waweru needs to import a car from Japan where cost is USD 5000 outside Kenya. He intends to buy the car through an agent who deals in Japanese yen. The agent will charge him 20% commission on the price of the car and further 80,325 Japanese yen for shipment of the car. How much Kenya shillings will he need to send to the agent to obtain the car given that?
1USD = 105.00 yen and 1USD = KSh. 63.00 (3 marks)
Cost of the car in USD
= 5000 + 20/100 x 5000
= 5000 + 1000
= USD 6000
If 1USD = 105 yen
? = 80,325
80325
105
= 765 USD
Total cost in US$ = 6765
Amount needed in KSh.
KSh. 63 x 6765
KSh. 426,195 - Use tables of reciprocals only to find the value of
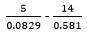 (3 marks)
(3 marks)
5 x 1 - 14 x 1
8.29 x 10-2 5.81 x 10-1
5 x 0.126 x 102 - 14 x
0.1721 x 10
= 60.3 – 24.094
= 36.206 - The figure below AB//CD, AD and BC intersect at T. Given that AT:TD = 1:3 and CB = 12cm. Calculate the length of TB. (3 marks)

a = x = 1
12 -a 3x 3
3a = 12 – a
4a = 12
A = 3cm
therefore: TB = 3cm - Draw the net of the solid shown below. (3 marks )

- The figure below shows a histogram. (3mks)

Fill in the table below the missing frequencies.
Length in x cm
Frequency
7.5 ≤ x ≤ 9.5
12
9.5 ≤ x ≤ 11.5
5 x 1.6 = 16 11.5 ≤ x ≤ 15.5
5 x 0.8 x 4 = 16 15.5 ≤ x ≤ 21.5
5 x 2 x 6 = 60 - Solve for x: (log2x )2 - Log2 x3 = 4 (4 marks)
Let log2x = y
y2 - 3y – 4 = 0
(y – 4) (y + 1 ) = 0
y = 4 or y = -1
log2x = 4 and log2x = 1
x = 16 or x = 1
2 - Mutua bought 8 pairs of trousers and six shirts at Sh. 4160. Had he bought twice as many shirts and half as many trousers, he would have saved Sh. 160. Find the cost of each item. (3 marks)
8t + 6s = 4160
4t + 12s = 40004t + 3s = 2080
t + 3s = 1000 -
3t = 1080
t = 360
s = 2131/3
Trouser = Sh. 360
Shirt = Sh. 213.33 - Two containers have base area of 750cm2 and 120cm2 respectively. Calculate the volume of the larger container in litres given that the volume of the smaller container is 400cm3. (3 marks)
A.S.F = 750/120 = 25/4
L.S.F = √(25/4) = 5/2V.S.F = (5/2)3 = 125/8
V.S.F = 125 = V
8 400cm2
V = 125/8 x 400 = 6250cm3
Volume in litres = 6250
1000
= 6.25L - In the figure below O is the centre of circle PQRS. ∠PTS = 56º and ∠PQS = 28º and TPQ is a straight line.

Find:- ∠TSP (2mark)
∠SPQ = 90º
∠TSP = 90º – 56º = 34º
∠PSQ = 90º – 28º = 62º
∠PRQ = ∠PSQ (Subtd by same chord)
∠PRQ = 62º - ∠PRQ (1 mark)
- ∠TSP (2mark)
- Simplify the following expression.
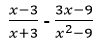 (3 marks)
(3 marks)
(x – 3)2 – (3x – 9)
(x + 3 (x – 3)
x2 – 6x + 9 – 3x + 9
(x + 3) (x – 3)
x2 – 9x + 18
(x + 3) (x – 3)(x – 3) (x – 6)
(x + 3) (x – 3)
x – 6
x + 3
SECTION II (50 marks)
- Three partners Mutua, Muthoka and Mwikali contributed Sh. 600,000, Sh. 400,000 and Sh. 800,000 respectively to start a business of a matatu plying Mbumbuni – Machakos route. The matatu carries 14 passengers with each paying Sh. 250. The matatu makes two round trips each day and ever full. Each day Sh. 6000 is used to cover running costs and wages.
- Calculate their net profit per day. (2 marks)
250 x 14 x 2 x 2 = 14000
Net profit = 14000 – 6000
= KSh. 8000 - The matatu works for 25 days per month and is serviced every month at a cost of KSh.10, 000. Calculate their monthly profit in June. (1 mark)
8000 x 25 = 200,000
= 190,000 - The three partners agreed to save 40% of the profit, 24% to be shared in the ratio of their contribution. Calculate Muthoka’s share in the month of July (4 marks)
Saving: 40/100 x 190,000
= 76000
Remaining profit = 36/100 x 190,000
= 68,400
Muthoka’s share
45,600/3 + 2/9 x 68,400
= 30,400 - The matatu developed mechanical problems and they decided to sell it through an agent who charged a commission of 5% on selling price. Each partner received KSh. 475,000 from the agent after he had taken his commission. Determine the price at which the agent sold the matatu. ( 3 marks)
475,000 x 3 x 10095
= 1,500,000
- Calculate their net profit per day. (2 marks)
- The income tax rates in a certain year are as shown below.
Omar pays Sh. 4000 as P.A.Y.E per month. He has a monthly house allowance of KSh.10800 and is entitled to a personal relief of KSh. 1,100 per month. Determine:Income (k₤ – p.a
Rate (KSh. per ₤)
1 – 4200
2
4201 – 8000
3
8001 – 12600
5
12601 – 16800
6
16801 and above
7
- his gross tax per annum in Kshs (2 Marks)
(4000 x 12) +(1100 x 12)
= Sh. 61,200 - his taxable income in K₤ per annum (2 marks)
1st slab 4200 x2= 8400
2nd slab 3800 x 3 = 11400
3rd slab 4600 x 5 = 23000 42800
4th slab x 6 = (61,200 – 42800)
= K₤ 3066.70
= Taxable income
(12600 + 3066.70
= K₤ 15666.7 - his basic salary in Ksh. per month. (2marks)
15666.7 x 20 - 10800
12
= KSh. 15,311.20 - his net salary per month (2 marks)
26111.20 – 4000
Sh. 22,311.20
- his gross tax per annum in Kshs (2 Marks)
-
-
- Fill the table below for the function.
y = 2x2 + 5x – 12 for -8 ≤ x ≤ 4 (2 marks)
B1 – For half + correct values B1B1 for all valuesx
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
2x2
128
98
72
50
32
18
8
2
0
2
8
18
32
5x
-4
-35
-30
-25
-20
-15
-10
-5
0
5
10
15
20
-12
-12
-12
-12
-12
-12
-12
-12
-12
-12
-12
-12
-12
-12
y
76
51
30
13
0
-9
-14
-15
-12
-5
6
21
40
- Using the table, draw the graph of the function y = 2x2 + 5x – 12. Use the scale 1cm to 1 unit on the x-axis and 1cm for 10 units for the y – axis (4 marks)
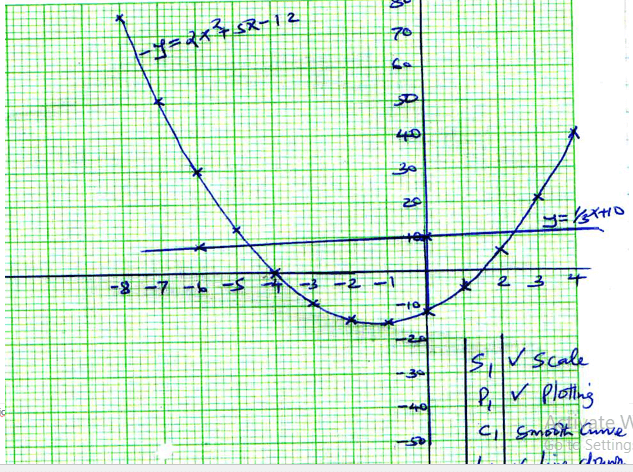
- Fill the table below for the function.
- Use the graph drawn above to solve the following equations.
- 2x2 + 5x – 12 = 0 (2 marks)
2x2 + 5x – 12 = y
2x2 + 5x – 12 = 0
0 = y
x = -4 or 1.5 - 3 – 7x – 3x2 = 0 (2 marks)
= 2x2 + 5x- 12 x -3
0 = -3x2 – 7x + 3 x 2
-3y = -6x2 – 15x + 36
0 = -6x2 – 14x + 6
-3y = -x - 30
y = 1/3 x + 10
x = -4.7 or 2.3
- 2x2 + 5x – 12 = 0 (2 marks)
-
- The diagram below shows the speed-time graph for a bus travelling between two stations. The bus begins from rest and accelerates uniformly for 30 seconds. It then travels at a constant speed for 60 seconds and finally decelerates uniformly for 40 seconds.

Given that the distance between the two stations in 2090m. Calculate- The maximum speed, in km/h the bus attained (3 Marks)
1/2 x 30h+ 1/2x40h+60h = 2090
95h = 2090
h = 22m/s
max speed = (22 x 3600)/1000
= 79.2 km/h - The acceleration (2 Marks)
a = 22/30
= 11/30 - The distance travelled during the last 20 seconds (2 Marks)
1/2 x 20 x 11 = 220/2
= 110m - The time the bus takes to travel the first half of the journey (3 Marks)
Time for half journey
1/2 x 22 (30 + t + t) = 1/2 x 2090
11 (30 + 2t) = 1045
330 + 22t = 1045
22t = 919
t = 32.5
- The maximum speed, in km/h the bus attained (3 Marks)
- In the figure below, K,L,M and N are points on the circumference of the circle centre O. The points K, O, M and P are on a straight line. PN is tangent to the circle at N. ∠KOL = 130º and ∠MKN = 40º.

Stating the reason in each case, find the values of the following angles,- MLN (2 marks)
40º – Angle subtended by the same
arc: MN - OLN (2 marks)
25º – Diameter of a circle subtends
90º at the circumference of a circle. - LNP ( 2 marks)
65º – Alternate segment theorem
(∠LNP is alternate to ∠LKN) - MPN ( 2 marks)
10º – Sum of angles in a triangle
add up to 18º - KNQ (2 marks)
50º – Alternate segment theorem or
sum of angles in a straight line add up to 180º .
- MLN (2 marks)
- The figure below shows a model of a solid in the shape of a frustum of a cone with a hemispherical top.

The diameter of the hemispherical top is 70cm and is equal to the diameter of the top of the frustum. The frustum has a base diameter of 28cm and a slant height of 60cm.- Calculate the area of the hemispherical surface. ( 1mark)
2πr2 = 2 x 22/7 x 35 x 35 = 7700cm2 - Calculate the slant height of the cone from which the frustum was cut. (4marks)

- Calculate the total surface area of the mode. (5 marks)
60+x = 35
x 14120 + 2x = 5x
x = 40cm
Slant height= 60 + 40 =100cm
πRL - πrl
22 x 35 x 100 - 22 x 14 x 40
7 7
11000 – 1760 = 9240cm2
Base area (πr2)
= 22/7 x 14 x 14 = 616cm2
Total surface area
7700 + 616 + 9240 = 17,556cm2
- Calculate the area of the hemispherical surface. ( 1mark)
- The figure below shows triangle OPQ in which OS = 1/3 OP and OR = 1/3 OQ. T is a point on QS such that QT = 3/4 QS

- Given that OP = p and OQ = q, express the following vectors in terms of p and q.
- SR (1 Mark)
OS = 1/3OP QT = 3/4OS OR = 1/3OQ
SR = SO + OR = 1/3P + 1/3Q
= 1/3(Q – P) - QS (2 Marks)
QS = QO + OS= Q + 1/3P
= 1/3P – Q - PT (2 Marks)
PT = PS + ST
= -2/3P + 1/4(-QS)= -2/3p + 1/4 (Q - 1/3P)
=-2/3p + 1/4q - 1/12p
=-9/12p + 1/4q = 1/4q - 3/4p - TR (2 Marks)
TR = TQ + QR= -3/4 QR - 2/3Q
= -3/4(1/3p – q) - 2/3Q
= -1/4p + 3/4q - 2/3q = - 1/4P + 1/12Q
= 1/12Q - 1/4P
PT = 1/4Q - 3/4P
TR = 1/12Q - 1/4P
therefore: PT = 3TR or 1/3PT = RT
- SR (1 Mark)
- Hence or otherwise show that the points P, T and R are collinear. (3 Marks)
Common point T
PT is a multiple of TR
PT = 3TR
Hence PTR are collinear
- Given that OP = p and OQ = q, express the following vectors in terms of p and q.
- The displacement S metres of a body moving along a straight line after t seconds is given by
S = -2t3 + 3/2 t2 + 3t- Find its initial acceleration. (3 marks)
Initial acceleration is at t = 0
V=ds/dt = - 6t^2 + 3t + 3
a = dv/dt = -12t + 3
when t = 0, a =[ 0 + 3 ]
therefore: a = 3m/s2 - Calculate:-
- The time when the body was momentarily at rest. (3 marks)
at rest V = 0
-6t2 + 3t + 3 = 0
(2t + 1) (t-1) = 0
t = -1/2 or t = 1 (t = -1/2 not applicable) - Its displacement by the time it comes to rest momentarily (2 marks)
S = -2t3 + 3/2 t2 + 3t
When t =m 1, s = -2(1)3 + 3/2 (1)2 + 3 (1)
2.5M
- The time when the body was momentarily at rest. (3 marks)
- Calculate the maximum velocity attained (2 marks)
When velocity is maxium, a = 0
-12t + 3 = 0
t = 1/4
Max v = -6 (1/4)2 + 3(1/4) + 3 = 3.375 m/s
- Find its initial acceleration. (3 marks)
Download Mathematics P1 Questions and Answers - Momaliche 4 cycle Post Mock Exams 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

