Instructions to candidates
- Write your name and index number in the spaces provide above
- Sign and write the date of examination in the spaces provided above
- This paper consists TWO section:Section I and Section II.
- Answer all the Questions in Section I and Five questions from Section II.
- All answers and workings must be written on this paper.
For Examiners use only
Section I
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Total |
Section II
|
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
Total |

QUESTIONS
SECTION 1 : 50 MKS
- Use logarithm tables only, giving your answer corrected to three significant figures ; to evaluate (4mks)
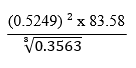
- Make K the subject of the formula. (3mks)
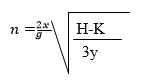
- Solve for θ in radians given. (3mks)
2 Cos 2θ + 1 = 0 for 0 ≤ θ≤ 2 πC - Atieno was asked to round off
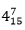 to 3 decimal places but she truncated it instead to 3 decimal places. Calculate.
to 3 decimal places but she truncated it instead to 3 decimal places. Calculate.
Her percentage error resulting from the misunderstanding. (3mks) - Ketepa tea worth Ksh 40 per kg is mixed with Sasini tea worth Ksh 60 per Kg in the ratio 3:1 . In what ratio should this mixture be mixed with Kericho tea worth Ksh 50 per kg to produce a mixture worth Kshs 47 per kg. (3mks)
- Calculate the length of a chord which is 3cm from the centre of the circle with radius 5cm. . (3mks)
- The position vectors of point A and B are a= -2i+j-8k and b= -3i+2j-2k respectively . Find the magnitude of AB. (3mks)
- Without the use of a calculator or mathematical tables, simplify. (3mks)
Sin 330º + Cos 120º
Tan 60º+ Cos 240º - The cash price of a music system is Ksh 30000. It can be bought under hire purchase terms by paying a deposit of ksh 10,000 and twelve monthly instalment of Ksh 3200 per month. Determine the percentage rate of interest per month. (3mks)
- Given that the coefficient of x3 in the expansion
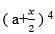 4 is 1
4 is 1- Find the value of a (2mks)
- Hence write down the first four terms of
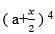 4 (2mks)
4 (2mks)
- The image of a scalene triangle under the transformation given by the matrix
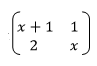 is a straight line. Find the possible value of x (3mks)
is a straight line. Find the possible value of x (3mks) - Use the mid ordinate rule to estimate the area bounded by the curve y+x2 = 4 and the line y = 0 using four strips . (3mks)
- State the centre and radius of the circle given by the following equation.
(x-4) 2 + (y+2)2 - 4 = 0 (2mks) -
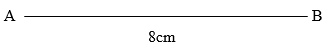
Use the line AB above to construct rectangle ABCD with BC = 5cm . A region R moves inside the rectangle under the following conditions- It is always nearer to AB than AD
- and always at least 3cm from point B
Locate R by shading the region. (3mks)
- The probability that John misses lunch at school is ¾ . If he misses lunch , the probability that he dozes off during the afternoon lessons is 4/7 . Otherwise his probability of dozing off in the afternoon is ½ .
- Illustrate the probabilities using a tree diagram. (1mk)
- Calculate the probability that John does not doze off during the afternoon lessons. (2mks)
- The first 4 terms of a G.P are 4,8,16,32
- Find the common ratio (1mk)
- Calculate the sum of the first 8 terms of the G.P (2mks)
SECTION II
Answer only five questions
-
- Complete the table below for the function y = 2 Cos 3x (2mks)
x
00
100
200
300
400
500
600
700
800
900
1000
1100
1200
Cos 3x
1.000
-
0.5000
-0.5000
-1.0000
-1.8660
0.5000
1.0000
y
2.00
1.00
-100
-2.00
-1.73
1.00
2.00
-
- Using the values in the completed table, draw the graph of y=2 Cos 3x for 0º≤ x ≤ 120º on the grid provided.

- Using the graph, solve the equation. 2 Cos 3x=0 (3mks)
- Using the values in the completed table, draw the graph of y=2 Cos 3x for 0º≤ x ≤ 120º on the grid provided.
- State the amplitude and period of the graph of y= 2 Cos 3x. (2mks)
- Complete the table below for the function y = 2 Cos 3x (2mks)
- Muma is standing 10 Km from a point P which is due North from her. She walks on a straight on a bearing of 0300 . By calculation, find
- How far will she have walked when she is equidistant from her starting point and P. (2mks)
- What is the bearing of P from this equidistant point. (2mk)
- How far will Muma have walked when she is at the shortest distance from the point p. (2mks)
- How far will the point P be from Muma when she walked 20 Km on the same straight path. (4mks)
- The height of a number of orange trees in an orchard were measured to the nearest (cm) and recorded in the table below.
Using an assumed mean of 165.5, calculate131 - 140
141 – 150
151 – 160
161 – 170
171 – 180
181 – 190
191 - 200
13
23
36
50
35
28
15
- The mean height (3mks)
- The standard deviation of the distribution (4mks)
- The quartile deviation (3mks)
- The points A (5,-1) B (1,-2) and C (x ,y) of a triangle are mapped onto A' (1,5) B'(2,1) and C'(4,2) by a matrix
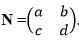 Find
Find- Matrix N of the transformation. (4mks)
- Co-ordinates of C (2mks)
- A" B" C” are the image of A' B'C' under a transformation represented by matrix
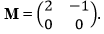
Write down the co-ordinates of A" B" C" (2mks) - A transformation N followed by M can be represented by a single transformation K. Determine K (2mks)
- A ship left port A (11º N, 32º W) and sailed due west to another port B. The journey took 160 hours at an average speed of 28 knots. Given that radius of the earth is 6370km and π = 22⁄7
- Calculate the distance between A and B
- In nautical miles (2mks)
- In km (2mks)
- Calculate the average speed of the ship in km/h correct to 2d.p (2mks)
- Calculate to the nearest whole number the longitude of port B and hence state its position (4mks)
- Calculate the distance between A and B
-
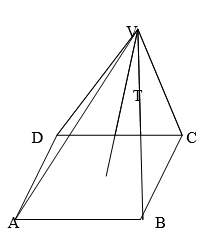
The right pyramid above (not drawn to scale) has AB = 12 cm and BC = 16 cm. O is the centre of the base with OV = 15 cm.
Calculate, giving your answer to four significant figures.- The length of the slant edge (2mks)
- The angle between the lines VA and VC (2mks)
- The angle between the plane ABV and the base ABCD (3mks)
- The pyramid is chopped at point T to form a frustum such T divides OV in the ration 2:1. Find the volume of the frustum. (3mks)
- The figure below shows the sketch of the curve y = x2 - 2x + 4and a straight line PQ which cuts the x-axis and the y-axis at the points (10, 0) (0, 10) respectively.
The line also intersects the curve at P and Q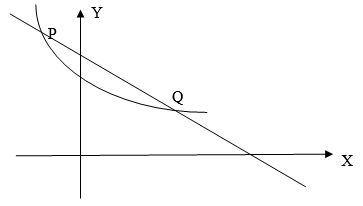
Find.-
- The equation of the straight line in the form y = m x + c (2mks)
- The co-ordinates of P and Q (4mks)
- Use integration to find the area of the shaded part. (4mks)
-
- Owiti makes two types of dresses, A and B. He takes 3 hours to make one pair of type A and 4 hours to make one pair of type B. He works for a maximum of 120 hours to make x pairs of type A and Y pairs of type B. It costs him shs 400 to make a pair of type A and shs. 150 to make a pair of type B. His total cost does not exceed shs. 9000. He must make at least 8 pairs of type A and more than 12 pairs of type B.
- Write down four inequalities representing the above information. (4mks)
- On the grid provided, draw the inequalities and shade the unwanted region. (3mks)

- Owiti makes a profit of shs. 40 on each pair of type A and shs. 70 on pair of type B dresses. Use the graph in part (b) above to above determine the maximum possible profit he makes. (3mks)

MARKING SCHEME
SECTION 1 : 50 MKS
- Use logarithm tables only, giving your answer corrected to three significant figures ; to evaluate (4mks)
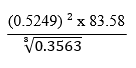
No Log 0.52492
83.58
3√0.3563
101 × 3.247
=32.51.7200
×2
1.4400
1.9221 +
1.3621
1.5518 = 3 + 2.5518
3 3 3
1.8505
1.5115 - Make K the subject of the formula. (3mks)
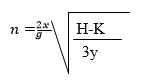
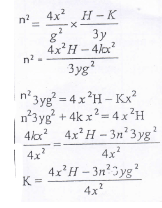
- Solve for θ in radians given. (3mks)
2 Cos 2θ + 1 = 0 for 0 ≤ θ≤ 2 πC
2 cos 2θ + 1 = 0
cos 2 θ = -0.5
2θ = 120º,240º,480º,600º
θ= 60º, 120º, 240º
π , 2π, 4π
3 3 3 - Atieno was asked to round off
 to 3 decimal places but she truncated it instead to 3 decimal places. Calculate.
to 3 decimal places but she truncated it instead to 3 decimal places. Calculate.
Her percentage error resulting from the misunderstanding. (3mks) = 4.4666667
= 4.4666667
actual = 4.4667
truncation = 4.467
error = 4.467 - 4.66 = 0.001
%error = 0.001 × 100
4.4667
= 0.0223863% - Ketepa tea worth Ksh 40 per kg is mixed with Sasini tea worth Ksh 60 per Kg in the ratio 3:1 . In what ratio should this mixture be mixed with Kericho tea worth Ksh 50 per kg to produce a mixture worth Kshs 47 per kg. (3mks)
40 × 3 + 60 × 1 = 120 + 60 = 45/= per kg
4 4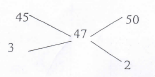
=3:2 - Calculate the length of a chord which is 3cm from the centre of the circle with radius 5cm. . (3mks)
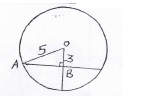
AB = √52 - 32
= 4
length = 4 × 2
= 8 cm - The position vectors of point A and B are a= -2i+j-8k and b= -3i+2j-2k respectively . Find the magnitude of AB. (3mks)
AB = AO + OB
=(2i - j + 8k) + (-3i + 2j - 2k)
= -i + j + 6k
(AB) = √(-1)2 + (1)2 + (6)2
= √38
= 6.164 - Without the use of a calculator or mathematical tables, simplify. (3mks)
Sin 330º + Cos 120º
Tan 60º+ Cos 240º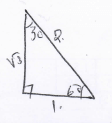
tan 60º = √3
Cos 240º = -½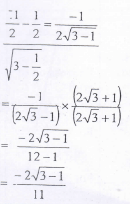
- The cash price of a music system is Ksh 30000. It can be bought under hire purchase terms by paying a deposit of ksh 10,000 and twelve monthly instalment of Ksh 3200 per month. Determine the percentage rate of interest per month. (3mks)
total monthly installments = 3200 × 12
= 38400
principal = 30000 - 10000
= 20000
38400 = 20000 (1 + r/100)12
log 1.92 = 12 log (1 + r/100)
1.059 = 1 + r/100
r = 5.9% - Given that the coefficient of x3 in the expansion
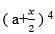 4 is 1
4 is 1- Find the value of a (2mks)
a4 + 2a3x + 3/2a2x2 + ax3/2 + x4/16
a/2 = 1
a = 2 - Hence write down the first four terms of
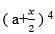 4 (2mks)
4 (2mks)
24 + 24x + 3/2x4x2 + x3
16 + 16x + 6x2 + x3
- Find the value of a (2mks)
- The image of a scalene triangle under the transformation given by the matrix
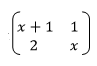 is a straight line. Find the possible value of x (3mks)
is a straight line. Find the possible value of x (3mks)
det = 0
x(x + 1) - 2 = 0
x2 + x - 2 = 0
(x + 1) (x - 2) = 0
x = 1 or +2 - Use the mid ordinate rule to estimate the area bounded by the curve y+x2 = 4 and the line y = 0 using four strips . (3mks)
area = 1(1.75 + 3.75 + 3.75 + 1.75)x -1.5 -0.5 0.5 1.5 y 1.75 3.75 3.75 1.75
= 11sq. units - State the centre and radius of the circle given by the following equation.
(x-4) 2 + (y+2)2 - 4 = 0 (2mks)
(x - 4)2 + (y - 2)2 - 4 = 0
center (4,-2)
radius = √42 + (-2)2 + 4
= √24 units -
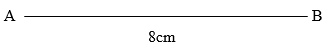
Use the line AB above to construct rectangle ABCD with BC = 5cm . A region R moves inside the rectangle under the following conditions- It is always nearer to AB than AD
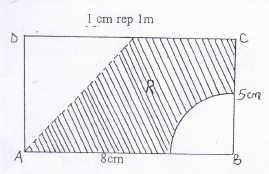
- and always at least 3cm from point B
Locate R by shading the region. (3mks)
- It is always nearer to AB than AD
- The probability that John misses lunch at school is ¾ . If he misses lunch , the probability that he dozes off during the afternoon lessons is 4/7 . Otherwise his probability of dozing off in the afternoon is ½ .
- Illustrate the probabilities using a tree diagram. (1mk)
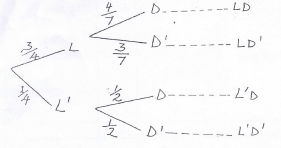
- Calculate the probability that John does not doze off during the afternoon lessons. (2mks)
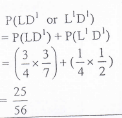
- Illustrate the probabilities using a tree diagram. (1mk)
- The first 4 terms of a G.P are 4,8,16,32
- Find the common ratio (1mk)
r = 8/4 = 2B1
sn = a(rn - 1) = 4(28 - 1)
r - 1 1
4 × 255
1020 - Calculate the sum of the first 8 terms of the G.P (2mks)
- Find the common ratio (1mk)
SECTION II
Answer only five questions
-
- Complete the table below for the function y = 2 Cos 3x (2mks)
x
00
100
200
300
400
500
600
700
800
900
1000
1100
1200
Cos 3x
1.000
-
0.5000
-0.5000
-1.0000
-1.8660
0.5000
1.0000
y
2.00
1.00
-100
-2.00
-1.73
1.00
2.00
-
- Using the values in the completed table, draw the graph of y=2 Cos 3x for 0º≤ x ≤ 120º on the grid provided.
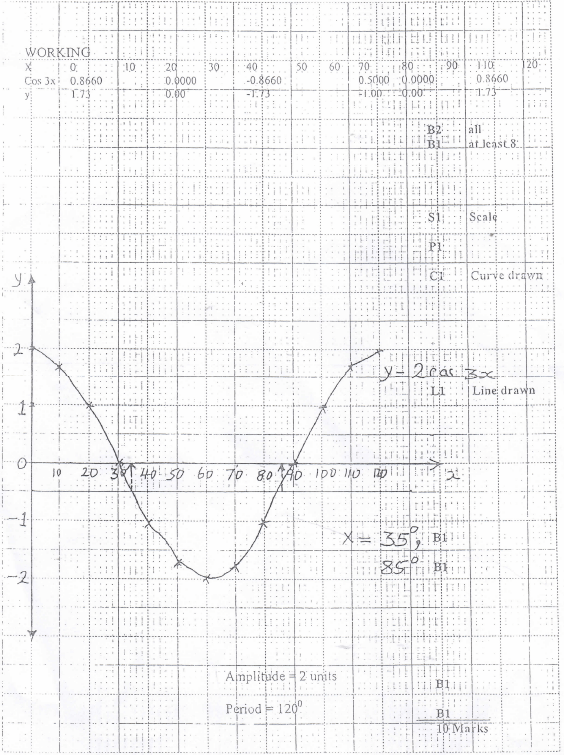
- Using the graph, solve the equation. 2 Cos 3x=0 (3mks)
- Using the values in the completed table, draw the graph of y=2 Cos 3x for 0º≤ x ≤ 120º on the grid provided.
- State the amplitude and period of the graph of y= 2 Cos 3x. (2mks)
- Complete the table below for the function y = 2 Cos 3x (2mks)
- Muma is standing 10 Km from a point P which is due North from her. She walks on a straight on a bearing of 0300 . By calculation, find
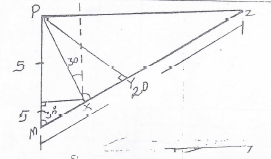
- How far will she have walked when she is equidistant from her starting point and P. (2mks)
cos 30 = s
MX
mx = 5
cos 30
= 5.774 - What is the bearing of P from this equidistant point. (2mk)
360º - 30º
=330º - How far will Muma have walked when she is at the shortest distance from the point p. (2mks)
cos 30 = MY
10
my = 10cos 30º
= 10 × 0.8660
= 8.66m - How far will the point P be from Muma when she walked 20 Km on the same straight path. (4mks)
by cosine rule:
x2 - 102 + 202 - 2 × 200cos 30º
= 500 - 400cos 30º
= 500 - 346.41
=153.59
x = 12.39
- How far will she have walked when she is equidistant from her starting point and P. (2mks)
- The height of a number of orange trees in an orchard were measured to the nearest (cm) and recorded in the table below.
Using an assumed mean of 165.5, calculateheight(cm) frequency c.f 131 - 140
141 – 150
151 – 160
161 – 170
171 – 180
181 – 190
191 - 200
13
23
36
50
35
28
15
13
36
72
122
157
185
200
- The mean height (3mks)
x = A + Σfdx x - A fx 135.5
145.5
155.5
165.5
175.5
185.5
195.5
-30
-20
-10
0
10
20
30
-390
-460
-360
0
350
560
450
Σfx = 150
Σf
165.5 + 150
200
165.5 + 0.75
166.25 - The standard deviation of the distribution (4mks)
s = √Σfd2 - (Σfd)2d2 fd2 900
400
100
0
100
400
900
11700
9200
3600
0
3500
11200
13500
Σ = 52700
Σf Σf
√ 52700 - (0.75)2
200
√263.5 - 0.5625
√262.9375
=16.215
16.22 - The quartile deviation (3mks)
Q3 - Q1
2
Q1= 1/4 × 200 = 50
178.5 - 154.388
2
150.5 + (50 - 36) × 10 = 154.3888
36
170.5 + (150 - 122) 10 = 178.5
35
=12.055
- The mean height (3mks)
- The points A (5,-1) B (1,-2) and C (x ,y) of a triangle are mapped onto A' (1,5) B'(2,1) and C'(4,2) by a matrix
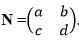 Find
Find- Matrix N of the transformation. (4mks)
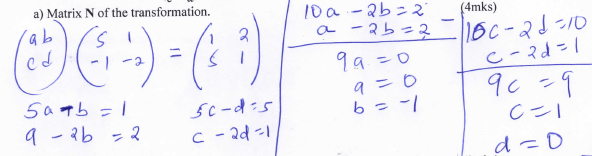
- Co-ordinates of C (2mks)
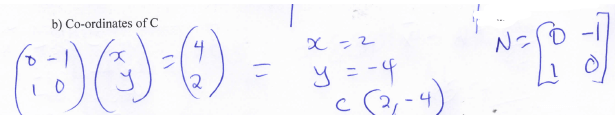
- A" B" C” are the image of A' B'C' under a transformation represented by matrix
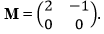
Write down the co-ordinates of A" B" C" (2mks)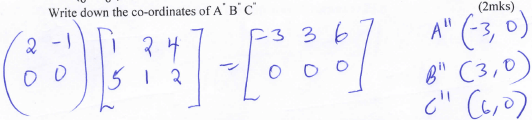
- A transformation N followed by M can be represented by a single transformation K. Determine K (2mks)
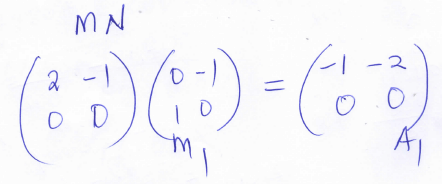
- Matrix N of the transformation. (4mks)
- A ship left port A (11º N, 32º W) and sailed due west to another port B. The journey took 160 hours at an average speed of 28 knots. Given that radius of the earth is 6370km and π = 22⁄7
- Calculate the distance between A and B
- In nautical miles (2mks)
D = s × T
28 × 160 = 4480nm - In km (2mks)
4480 × 1.853 = 8301.44 km
- In nautical miles (2mks)
- Calculate the average speed of the ship in km/h correct to 2d.p (2mks)
S = D
T
= 8301.44
160
= 51.88 km/h - Calculate to the nearest whole number the longitude of port B and hence state its position (4mks)
4480 = O × 60 × cos11
O = 4480
60 × 0.9816
= 76.06
= 76º
longitude diff = x - 32 = 76
x = 108º
(11ºN, 108ºW)
- Calculate the distance between A and B
-

The right pyramid above (not drawn to scale) has AB = 12 cm and BC = 16 cm. O is the centre of the base with OV = 15 cm.
Calculate, giving your answer to four significant figures.- The length of the slant edge (2mks)
AC = √122 + 182
=20 cm
AV = √102 + 152
√325
= 18.03 cm - The angle between the lines VA and VC (2mks)
Tan σ = 10 = 0.6667
15
σ = Tan-1 0.6667
= 33.69º - The angle between the plane ABV and the base ABCD (3mks)
vx = √18.032 - 62
= 17.00
cos B = 18
1700
β = cos-1 18
1700
β = cos-1 0.4706
β = 61.93º - The pyramid is chopped at point T to form a frustum such T divides OV in the ration 2:1. Find the volume of the frustum. (3mks)
1/3AH = 1/3 × 16 × 12 × 15 = 960cm3
1/3AH = 1/3 × 4 × 16/3 × 5 = 35.56 cm3
V of frustrum = 960 - 35.56
= 924.44cm3
- The length of the slant edge (2mks)
- The figure below shows the sketch of the curve y = x2 - 2x + 4and a straight line PQ which cuts the x-axis and the y-axis at the points (10, 0) (0, 10) respectively.
The line also intersects the curve at P and Q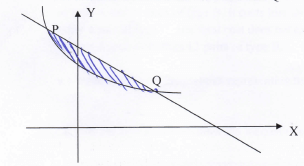
Find.-
- The equation of the straight line in the form y = m x + c (2mks)
a = Dy
Dx
a = 10 - 0
0 - 10
a = -1
-1 = y - 10
1 x - 0
y - 10 = -x
y = -x + 10 - The co-ordinates of P and Q (4mks)
y = x2 - 2x + 4 .........(i)
y = -x + 10
-x + 10 = x2 - 2x -2x + 4
x2 - 2x + x + 6 = 0
x2 - x + 6 = 0
x2 - x - 6 = 0
sum = -1
prd = -6
x2 + 2x - 3x - 6 = 0
x(x + 2) - 3(x + 2) = 0
x1 = 3
x2 = -2
P = (-2, 12)
Q = (3, 7)
- The equation of the straight line in the form y = m x + c (2mks)
- Use integration to find the area of the shaded part. (4mks)

-
- Owiti makes two types of dresses, A and B. He takes 3 hours to make one pair of type A and 4 hours to make one pair of type B. He works for a maximum of 120 hours to make x pairs of type A and Y pairs of type B. It costs him shs 400 to make a pair of type A and shs. 150 to make a pair of type B. His total cost does not exceed shs. 9000. He must make at least 8 pairs of type A and more than 12 pairs of type B.
- Write down four inequalities representing the above information. (4mks)
- On the grid provided, draw the inequalities and shade the unwanted region. (3mks)
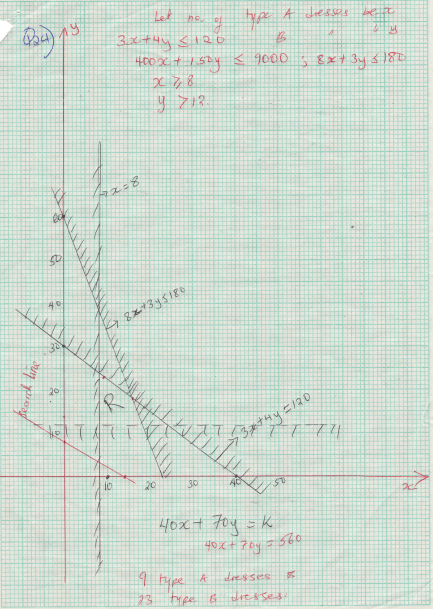
- Owiti makes a profit of shs. 40 on each pair of type A and shs. 70 on pair of type B dresses. Use the graph in part (b) above to above determine the maximum possible profit he makes. (3mks)
Download Mathematics P2 Questions and Answers - Momaliche 4 cycle Post Mock Exams 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

