Mathematics Paper 1 Questions and Answers - MECS Pre Mock Exams 2023

Next Topic »
Mathematics Paper 2 Questions and Answers - MECS Pre Mock Exams 2023

Download PDF for future reference Get on Whatsapp for 50/-

Instructions to Candidates

The paper contains TWO sections: Section I and II
Answer ALL questions in section I and STRICTLY ANY FIVE questions from section II.
All working and answers must be written on the question paper in the spaces provided below each question.
Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
Marks may be awarded for correct working even if the answer is wrong.
Non-programmable silent electronic calculators and KNEC Mathematical tables may be used except where stated otherwise.

For Examiner’s use only
Section I

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	TOTAL

Section II

17	18	19	20	21	22	23	24	TOTAL

QUESTIONS

SECTION I(50marks)

Answer all the questions in this section

The sum of four consecutive odd integers is less than 64. Determine the first four such integers. (3 marks)
Solve the equation (3marks)
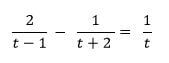
Moses has twenty shillings more than Jane. After he spends a quarter of his money and Jane ⅕ of hers, they find that Jane has 10 shillings more than Moses. How much money did both have? (4 marks)
The sum of interior angles of two regular polygons of side n-1 and n are in the ratio 4:5. Calculate;
1. The size of interior angle of the polygon with side (n-1) (2 marks)
2. The size of exterior angle of the polygon with side (n-1) (1 mark)
The figure below is a rhombus ABCD of sides 4cm. BD is an arc of circle center C. Given that ∠ABC = 138º. Find the area of shaded region correct to 3 significant figures. (Take π=22/7) (3 marks)
Find the greatest common factor of x³ y² and 4xy⁴. Hence factorise completely the expression x³ y²- 4xy⁴ . (3 Marks)
The figure below is a part of the sketch of a triangular prism ABCDEF.

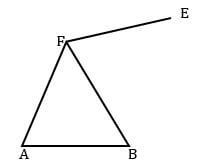
Complete the sketch by drawing the hidden edges using broken lines. (3 marks)
Without using calculator, solve for n in the equation 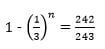(3marks)
Given that 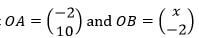and that the magnitude of AB is 13 units, find the possible values of x. (3marks)
Ali travelled a distance of 5km from village A to village B in direction of N600E. He then changed direction and travelled a distance of 4km in the direction of 1350 to village C.
1. Using a scale of 1cm to represent 1.0 km represent the information on an accurate diagram.(2marks)
2. Using scale drawing in (a) above determine
  1. The distance between A and C (1mk)
  2. The bearing of A from C (1mk)
Three numbers p,q and r are such that p³×q²×r=2250. Find p, q and r. (3 marks)
A bus starts off from Kitale at 9.00 a.m and travels towards Kakamega at a speed of 60km/hr. At 9.50 a.m, a matatu leaves Kakamega and travels towards Kitale at a speed of 60Km/h. If the distance between the two towns is 150km, how far from Kitale will the two vehicles meet? ( 3marks)
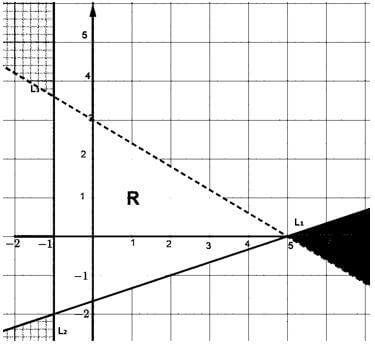
Find the inequalities that satisfy the region R shown in the figure below. (3 marks)
A dealer sells a certain spare part for Kshs 650, making a profit of 30%. The manufacturer reduces the price to the dealer by Kshs 50 and the dealer reduces his selling price by the same amount. Find the dealer’s new percentage profit.(3marks)
A taxi travelling at 20m/s accelerates uniformly and in 4 seconds, its velocity is 30m/s. it maintains this velocity for another 5 seconds before decelerating uniformly to rest after 3 seconds. Calculate the total distance travelled by the taxi during the journey. (3marks)
The length of a rectangle is (x+3) cm. If the width of the rectangle is two thirds its length and the perimeter is 40 cm, find its width. (3 marks)

SECTION II
Answer only five questions in this section

A sales agents earns a basic salary of Kshs. 20,000 per month. In addition, he is entitled for a commission for sales in excess of Kshs. 200,000 as follows:

Sales

Commission

0-200,000

0%

200,001-300,000

1.5%

300,001-400,000

3.0%

400,001-500,000

4.5%

Above 500,000

6.0%
1. On the month of April 2019, her total sales were Kshs. 558,200. Determine his total earnings that month. (4marks)
2. On the month of May 2020, his sales increase in the ratio 6:5, Calculate his total earnings on May 2020 to the nearest shilling. (3marks)
3. On the month of June 2020 his total earnings were Kshs. 39,800. Calculate the difference in his total sales in months of May and June. (3marks)
1. A man standing 20m away from a building notices that the angles of elevation of the top and bottom of a flagpole mounted at the top of the building are 640 and 620 respectively. Calculate to 1d.p. the height of the flagpole. (4marks)
2. The angles of elevation of the top of a tree from P and Q which are 30m apart are 220 and 320 respectively. Given that the two points are on the same side of the tree and on a Straight line, determine the height of the tree. (6marks)
Two security personnel were together at a road junction. Each had a walkie talkie. The maximum distance at which one could communicate with the other was 2.5km. One of the personnel walked due East at 3.2km/h while the other walked due North at 2.4km/h. The personnel who headed east travelled for x km while the one who headed North travelled for y km before they were unable to communicate.
1. Draw a sketch to represent the relative positions of the policemen. (1 mark)
2. 1. From the information above form two simultaneous equations in form of x and y. (2 marks)
  2. Find the value of x and y. (5 marks)
  3. Calculate the time in minutes taken before the security personnel were unable to communicate. (2 marks)
ABCD is a rectangle with A as the point (-3,1).
1. If AB is parallel to the line3y-x=4, find the equation of line AB. (2 marks)
2. Find the equation of line AD. (2marks)
3. If C has coordinates (2,6), find the equations of the line BC and CD in the form 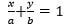(4marks)
4. Find the coordinates of B (2marks)
The figure below shows a rectangular sheet of metal whose length is twice its width.
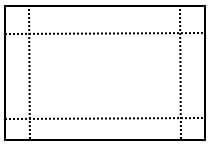
1. An open rectangular tank is made by cutting equal squares of length 60 cm from each of its four corners and folding along the dotted lines shown in the figure above. Given that the capacity of the tank so formed is 1920 litres and the width of the metal sheet used was x cm;
  1. Express the volume of the tank formed in terms of x cm. (3 marks)
  2. Hence or otherwise obtain the length and width of the sheet of metal that was used. (3 marks)
2. If the cost of the metal sheet per m² is Kshs 1000 and labour cost for making the tank is 300 per hour. Find the selling price of the tank in order to make a 30% profit if it took 6 hours to make the tank. (4 marks)
1. The ratio of Juma’s and Akinyi’s earnings was 5:3. Juma’s earnings rose to Ksh 8 400 after an increase of 12%. Calculate the percentage increase in Akinyi’s earnings given that the sum of their earnings was Ksh. 14 100 (6 marks)
2. Juma and Akinyi contributed all the new earnings to buy maize at Ksh 1 175 per bag. The maize was then sold at ksh 1 762.50 per bag. The two shared all the money from the sales of the maize in the ratio of their contributions. Calculate the amount that Akinyi got. (4 marks)
1. Given that 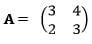find inverse of A (1mark)
2. Two colleges, Utalii and Huduma purchased beans and rice . Utalii bought 90 bags of beans and 120 bags of rice for a total of sh 360 000 . Huduma bought 200 bags of beans and 300 bags of rice for a total of sh 850 000. Use the inverse of A obtained in (a) above to find the price of one bag of each item. (6marks)
3. The price of beans later decreased in the ratio 4: 5 while that of rice increased by 20 %. A businessman bought 20 bags of beans and 30 bags 0f rice. How much did he pay? (3marks)
The figure below shows a model of a solid in the shape of a frustum of a cone with a hemispherical top.

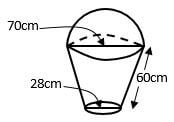
The diameter of the hemispherical top is 70cm and is equal to the diameter of the top of the frustum. The frustum has a base diameter of 28cm and a slant height of 60cm.
1. Calculate the area of the hemispherical surface. ( 1mark)
2. Calculate the slant height of the cone from which the frustum was cut. (4marks)
3. Calculate the total surface area of the model. (5 marks)

MARKING SCHEME

x + x + 2 + x + 4 + x + 6 < 64
4x < 48
x < 12
11, 13, 15, 17
2t + 4 - t + 1 = 1
(t - 1)(t + 2) t
t + 5 = 1
t² + t - 2 t
t² + 5t = t² + t - 2
4t = -2
t = ^-1/₂
Before spending
moses = 20 + x
Jane = x
After spending
moses = 60/4 + 3/4x
Jane = 4/5x

$/5x - (60/4 + 3/4x) = 10
4/5x - 60/4 + 3/4x = 10
x/20 = 25
x = 500
Jane = 500
moses = 520
1. (2(n - 1) - 4) 90 = 4
  (2n - 4)90 5
  2n - 6 = 4
  2n - 4 5
  2(n - 3) = 4
  2(n - 2) 5
  5n - 15 = 4n - 8
  n = 7
  (2(7 - 1) - 4)90 = 120º
  7 - 1
2. 180 - 120 = 60º
Area of rhombus = (1/2 x 4²sin42º) x 2
= 10.71 cm²Area of sector = 42/360 x 22/7 x 4² = 5.867cm²
shaded area = 10.71 - 5.867
= 4.56 cm²
GCD = xy²
= xy²(x² - 4y²)
= xy² (x² - (2y)²)
= xy²(x - 2y)(x - 2y)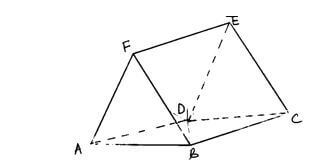
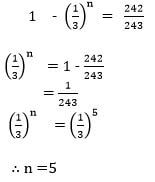
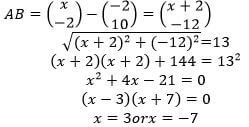
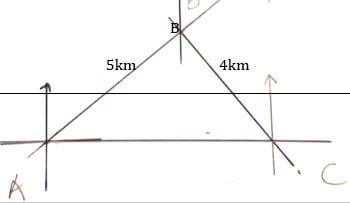
2. 1. 7 km
  2. 226º
2 2250

3 1125

3 375

5 125

5 25

5 5

1

P³ x q² x r = 5³ x 3² x 2
p = 5 q = 3 and r = 2
At 9.50 am, the bus has travelled
50/60 x 60 = 50 km
The distance between the two vehicles at 9:50 am
(150 - 50)
= 100 km
Rel. speed = 120 km/h
Time taken to meet = 100/120 hrs
Distance covered by the bus
= 50 / 60 x 60 = 50 km
Distance from kitale to the meeting point = 50 + 50 = 100 km
L1 ⇒ 3y ≥ x - 5
L2 ⇒ x ≥ -1
L3 ⇒ 5y < -3x + 15
old buying price = 650 x 100 = 500
130
new buying price = 500 - 50 = 450
new selling price = 650 - 50 = 400
%profit = 600 - 450 x 100
450
= 33.33%
Distance = area under the curve
= (1/2 x 4 (20 + 30) + 5 x 30 + (1/2 x 3 x 30)m
= 100 + 150 + 45
= 295 m
L = (x + 3)
W = 2/3 (x + 3) = 2/3x + 2
20 = (x + 3) + (2/3x + 2)
15 = x + 2/3x
x = 15 x 3 = 9 cm
5
width = 2/3(9) + 2 = 8 cm
1. commission
  1st bracket = 0
  2nd bracket = 1.5/100 x 100000 = 1500
  3rd bracket = 3/100 x 100000 = 3000
  4th bracket = 4.5/100 x 100000 = 4500
  5th bracket = 6/100 x 58200 = 3492
  Total commission = 1500 + 3000 + 4500 + 3492 = 12492
  Total earnings = 12492 + 20000 = 32492
2. may sales = 558200 x 6
  5
  = 669840
  New commission (5th bracket) = 169840 x 6/100
  = 10190.40
  Total commission
  = 1500 + 3000 + 4500 + 10190.40 = 19190.40
  Total earnings = 19190.40 + 20000 = 39190.40
  = 39190
3. Commission on the 5th bracket
  = 39800 - 20000 - (1500 + 3000 + 4500) = 10800
  sales on 5th bracket = 10800 x 100
  6
  = 180000
  Total sales for June = 500000 + 180000
  = 680000
  Difference = 680000 - 669840 = 10160
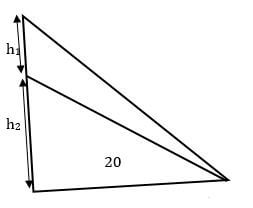
1. Tan 64 = h1 + h2
  20
  h1 + h2 = 20 tan 64
  h1 + h2 = 41.006
  
  Tan 62 = h2/20
  h2 = 20 tan 62
  h2 = 37.61
  h1 = 41.006 - 37.61 = 3.396
  height of plagpost = 3.4
2. tan 32 = h/x
  h = x tan 32
  tan 22 = h
  x + 30
  h = (x + 30) tan 22
  h = x tan 32 = (x + 30) tan 22
  0.6249x = (x + 30)0.4040
  0.2209x = 12.12
  x = 54.866
  h = 54.866 tan 32
  h = 34.28
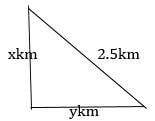
2. 1. 6.25 = x² + y²
    y/2.4 = x/3.2
    x = ^3.2/_2.4y
  2. 6.25 = x² + (^2.4/_3.2 x)²
    6.25 = 576/10.24x² + x²
    x² = 6.25/1.5625
    x² = 4
    x = 2
    
    y² + 2² = 6.25
    y² = 6.25 - 4
    y = 1.5
  3. Time = 2/3.2
    = 0.625 hrs
    = 37.5 minutes
1. 3y - x = 4
  y = 1/3x + 4/3
  m1 = 1/3
  m2 = 1/3
  y - 1 = 1
  x + 3 3
  y = 1/3x + 2
2. y - 1 = -3
  x + 3
  y = -3x - 8
3. Equation of BC
  y - 6 = -3
  x - 2
  y = -3x + 12
  x/4 + y/12 = 1
  Equation of CD
  y - 6 = 1
  x - 2 3
  3y = x + 16
  -x + 3y = 1
  16 16
4. coordinates of B
  (y = -3x + 12)3
  3y = x + 6
  3y = x + 6
  3y = -9x + 36
  0 = 10x - 30
  x = 3
  y = -3(3) + 12
  y = 3
  B(3,3)
1. 1. length = 2x - 120
    width = x - 120
    volume = (2x - 120)(x - 120)60
    = (2x² - 240x - 120x + 14400)60
    = 120x² - 14400x - 7200 + 864000
    120x² - 21600x + 864000
  2. Volume = 1920 000 cm₃
    (2x – 120) (x – 120) 60 = 1,920, 000
    (2x – 120) (x – 120) = 32 000
    2x² – 240x – 120x +14400 = 32 000
    2x² – 240x – 120x = 17600
    x² – 180x – 8800 = 0
    
    Either x = 220 or -40
    x is not equal to -40
    x = 220 cm
    Length = 440 cm
2. Area of sheet = 440 x 220
  = 96 800 cm²
  = 96 800 = 9.68 m²
  10000
  cost = 9.68 x 1000
  = sh 9680
  labour = 300 x 6 = sh 1800
  total cost = 9680 + 1800
  =Sh 11480
  S.P = 130/100 x sh.11480
  = sh 14924
1. Juma's earning before increase:
  112% → 8400
  100% → 8400 x 100/112 = 7500
  Akinyi's earning before increase; 3/5 x 7500
  Increase in Akinyi's earnings
  = 14100 - 8400 = 5700
  5700 - 4500 = 1200
  % increase in akinyi's earnings
  = 1200/4500 x 100
  = 26²/₃ = 26.67
2. No. of bags bought
  = 14100/1175
  = 12 bags
  Priofit = (1762.50 - 1175) x 12
  = 7050
  ratio 5700: 8400 = 19: 28
  Profit Akinyi : 7050 x 19/47 = 2850
  total earning for Akinyi
  5700 + 2850 = 8550
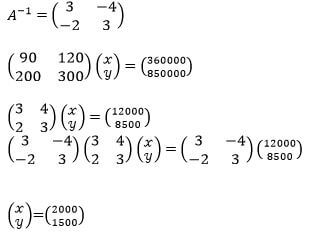
cost of 1 bag of beans sh.2000
cost of a bag of rice sh.1500
c). cost of 1 bag of beans = 2000 x 4/5
= 1600
cost of 1 bag of rice = 1500 x 120/100
= 1800
1600 x 20 + 1800 x 30
= sh. 86000
1. 2πr² = 2 x 22/7 x 35 x 35 = 7700cm²
2. 60 + x = 35
  x 14
  120 + 2x = 5x
  x = 40cm
  slant height = 60 + 40
  = 100 cm
3. πRL - πrl
  22/7 x 35 x 100 - 22/7 x 14 x 40
  11000 - 1760 = 9240cm²Base area (πr²)
  = 22/7 x 14 x 14 = 616cm²
  Total surface area
  7700 + 616 + 9240 = 17556cm²