INSTRUCTIONS TO CANDIDATES:
- The paper contains two sections. Section I and Section II.
- Answer ALL the questions in section I and any five questions in section II.
- Answers and working must be written on the question paper
- Show all steps in your calculations below each question.
- Marks may be given for correct working even if the answer is wrong.
- Non programmable silent electronic calculators and KNEC mathematical table may be used, except where stated otherwise.
FOR EXAMINERS USE ONLY
SECTION I
|
Question |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
TOTAL |
|
Marks |
SECTION II
|
Question |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
TOTAL |
|
Marks |

QUESTIONS
Section I (50 Marks)
Answer ALL questions in this section in the spaces provided
- Solve for x
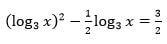 [4marks]
[4marks] - In the figure below PT is a tangent to the circle from an external point P. PT=24 cm and OP= 25 cm.
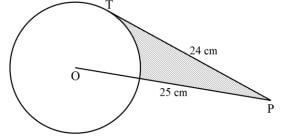
Calculate the area of the shaded region correct to 2 decimal places [4marks] - Find the value of w in the expression
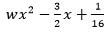 is a perfect square , given that w is a constant [2marks]
is a perfect square , given that w is a constant [2marks] - Simplify
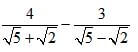 (3 marks)
(3 marks) - The cost C of hiring a conference facility for one day consists of two parts, one which is fixed and the other varies as the number of participants n attending the conference. If Kshs 45000 is charged for hiring the facility for 100 participants and Kshs 40000 for 60 participants, Find the number of participants if 63000 is used to hire the facility [3marks]
- Juma a form 2 student was told to pick two number x and y from a set of digits 0, 1, 2, 3, 4, 5 and 6. Find the probability that |x-y| is atleast 3. [3marks]
- Given that the matrix
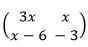 maps a triangle A(0,0), B(2,1) and c(3,5) on to a straight line. Find the possible values of x. [3marks]
maps a triangle A(0,0), B(2,1) and c(3,5) on to a straight line. Find the possible values of x. [3marks] - The points with co-ordinates A(13,3) and B(-3,-9) are the end of diameter of a circle centre O. Determine ;
- The coordinates of O [1mark]
- The equation of the circle expressing it in the form
x2+y2+ax +by +c=0 [3marks]
- Two containers have base areas of 750cm2 and 120cm2 respectively. Calculate the volume of the larger container in litres given that the volume of the smaller container is 400cm3.(3 marks)
- The cash price of a laptop is 4800. Wambui bought it on hire purchase by making a deposit of kshs. 10000 followed by 24 monthly instalments of kshs 2000 each. Calculate the monthly rate at which compund interest was charged [3marks]
- A merchant blends 350kg of KAKUZI tea costing shs. 84 per kg with 140 kg of KETEPA tea costing sh.105 per kg. calculate the price at which he must sell 1kg of the mixture to attain 20 % profit. [3marks]
- The graph below is part of the straight line graph obtained from the initial equation V=aPn
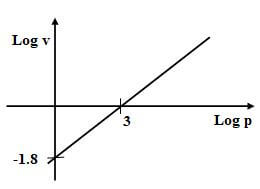
Write down the equation of a straight line in the form of y=mx+c hence use the graph to find the of a and n [3marks] - State the amplitude, period and phase angle of
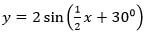
- Amplitude (1 mark)
- Period (1 mark)
- Phase angle (1 mark)
- Given the position vectors (OA) =4i +8j-2k and (OB) =3k-i-2j. Point C divides vector AB in the ratio of 3:-1. Find the magnitude of (OC) . Give your answer to 2dp [3marks]
- The table below shows income tax rates in a certain year
In a certain month of the year Mr. Mogaka had a total deduction of ksh5,000, he got a personal tax relief of kshs.1056 and paid kshs.3944 for NHIF, WCPS and sacco loan repayment. CalculateMonthly income in Kshs
Tax rate in each kshs
1 ≤ x < 9681
9681 ≤ x < 18801
18801 ≤ x < 27921
27921 ≤ x < 37040
Over 37040
10%
15%
20%
25%
30%
- P.A.Y.E. (1 mark)
- Monthly income/salary (3 marks)
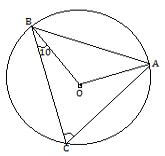
- In the figure given below, O is the centre of circle. If ∠BCA=80º and ∠CBO=10º.
Determine the size of ∠CAB. (3 marks) - In the figure below OB = b;OC = 3OB and OA = a
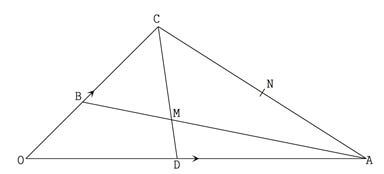
- Given that OD = 1/3OA and AN = 1/2AC , CD and AB meet at M. Determine in terms a and b
- AB (1 mark)
- CD (1 mark)
- Given that CM = kCD and AM = hAB. Determine the values of the scalars k and h. (5 marks)
- Show that O, M and N are collinear. (3 marks)
- Given that OD = 1/3OA and AN = 1/2AC , CD and AB meet at M. Determine in terms a and b
- The table below shows the marks scored by form four students in a mathematics test in Amani secondary school.
Using an assumed mean of 57Marks
Mid-point X
Frequency (f)
d = x - A fd d2 fd2 40-44
3
45-49
30
50-54
29
55-59
33
60-64
13
65-69
1
70-74
1
Σ f = Σ fd = Σ fd2 = - Complete the table (4 marks)
- Determine
- the mean mark (2 marks)
- The standard deviation (2 marks)
- Find the mark scored by the 50th student. (3 marks
- An arithmetic progression AP has the first term a and the common difference d.
- Write down the third, ninth and twenty fifth terms of the AP in terms of a and d. (2marks)
- The AP above is increasing and the third, ninth and twenty fifth terms form the first three consecutive terms of a geometric progression (G.P). The sum of the seventh and twice the sixth term of AP is 78. Calculate
- The first term and common difference of the A.P (5marks)
- The sum of the first 5 terms of the G.P (3marks)
-
-
- Taking the radius of the earth, R=6370km and π=22/7, calculate the shortest distance between two cities P(60ºN, 29ºW) and Q(60ºN, 31ºE) along the parallel of latitude. (3marks)
- If it is 1200hrs at P, what is the local time at Q (3marks)
- An aeroplane flew due south from a point A(600N, 450E) to a point B, the distance covered by the aeroplane was 8000km, determine the position of B. (4marks)
-
-
- Complete the table below to 2 decimal places. (2mks)
X
00
300
600
900
1200
1500
1800
2100
2400
2700
3000
3300
3600
– Cos x
– 1
– 0.5
0.5
0.87
0.87
-0.5
– 0.87
Sin ( x – 300)
0.0
0.5
0.87
0.5
– 0.5
– 0.87
– 0.5
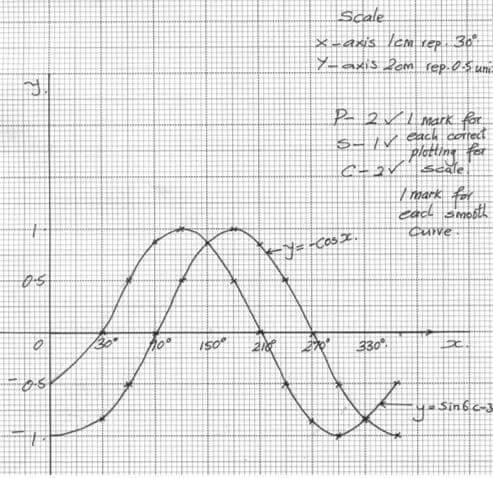
- Draw the graphs of y=sin (x – 30°) and y= – Cos x on the same axes, for 0º< x < 360º. (5mks)

- Use your graph to solve the equations
- sin (x – 30°) + Cos x = 0. (2marks)
- -Cos x=0.5 (1 marks)
- Complete the table below to 2 decimal places. (2mks)
- Kamau, Njoroge and Kariuki are practicing archery. The probability for Kamau hitting the target is 2/5 , that of Njoroge hitting the target is 1/4 and that of Kariuki hitting the target is 3/7.
Find the probability that in one attempt;- Only one hits the target (2marks)
- All three hit the target (2marks)
- None of them hits the target (2marks)
- Two hit the target (2marks)
- At least one hits the target (2marks)
- Figure below is a pyramid on a rectangular base. PQ=16cm, QR = 12cm and VP = 13cm.
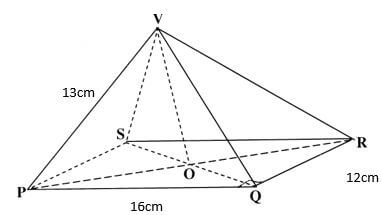
Find- The length of QS. (2marks)
- The height of the pyramid to 1 decimal place. (2marks)
- The angle between VQ and the base. (2marks)
- The angle between plane VQR and the base. (2marks)
- The angle between planes VQR and VPS (2marks)
- ABCD is a quadrilateral with vertices as follows: A (3, 1), B (2, 4) C (4, 3) and D (5, 1)
-
- On the grid provided draw the quadrilateral ABCD and the image A'B'C'D' under a transformation With matrix
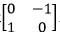 . Find the co-ordinates of A'B'C'D' (3marks)
. Find the co-ordinates of A'B'C'D' (3marks)
- Describe the transformation that maps ABCD onto A'B'C'D' fully (1mark)
- On the grid provided draw the quadrilateral ABCD and the image A'B'C'D' under a transformation With matrix
- A transformation represented by the matrix
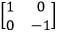 maps A'B'C'D' onto A''B''C''D'' find the co-ordinates of A''B''C''D''. Plot A''B''C''D'' on the same grid. (3marks)
maps A'B'C'D' onto A''B''C''D'' find the co-ordinates of A''B''C''D''. Plot A''B''C''D'' on the same grid. (3marks) - Determine a single transformation that maps A''B''C''D'' onto ABCD. Describe this transformation fully. (3marks)
-

MARKING SCHEME
- Let log3 x = y
y2 - 1/2y = 3/2
2y2 - y - 3 = 0
(2y - 3)(y + 1) = 0
y = 3/2 or y - 1
Log3x = 3/2 or log3x = -1
x = 33/2 or x = 3-1
x = 5.196 (or 3√3) or x = 1/3 - OT = √252 - 242 = 7 cm
< TOP = sin-1(24/25) = 73.74º
Area of shaded region
=1/2bh - θ/360 πr2
= 1/2 x 7 x 24 - 73.74/360 x 22/7 x 72
= 84 - 31.54
=52.46cm2 - b2 = 4ac
(-3/2)2 = 4 x w x 1/16
9/4 = w/4
w = 9 - 4(√5 - √2) - 3(√5 + √2)
(√5 + √2)(√5 - √2)
4√5 - 4√2 - 3√5 - 3√2
5 - 2
√5 - 7√2
3 - c = k + cn
45000 = k + 100x
40000 = k + 60x
5000 = 40x
x = 125
k = 32500
c = 32500 + 125n
63000 = 32500 + 125n
125n = 30500
n = 244 -
|x - y|x / y
0
1
2
3
4
5
6
0
0
1
2
3
4
5
6
1
1
0
1
2
3
4
5
2
2
1
0
1
2
3
4
3
3
2
1
0
1
2
3
4
4
3
2
1
0
1
2
5
5
4
3
2
1
0
1
6
6
5
4
3
2
1
0
P | x - y| ≥ 3 = 20/49 - -9x - x2 + 6x = 0
-x2 - 3x = 0
x2 + 3x = 0
x(x + 3) = 0
x = 0 or x = -3 -
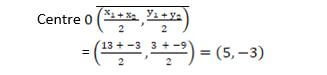
- Equation of circle
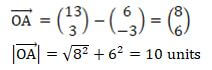 Equation
Equation
(x - 5)2 + (y - 3)2 = 102
x2 - 10x + 25 + y2 + 6y + 9 = 100
x2 + y2 - 10x + 6y + 25 + 9 - 100 = 0
x2 + y2 - 10x + 6y - 66 = 0
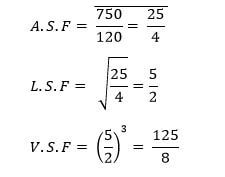
volume of larger = 125/8 x 400/1000
= 6.25 litres- p = 38000
A = 24 x 2000 = 48000
48000 = 38000 (1 + r/100)24
1.263 = (1 + r/100)24
1 + r/100 = 1.009781
r/100 = 0.009781
r = 0.9781% - cost price per kg = 350 x 84 + 140 x 105
350 + 140
= sh 90
selling price per kg = 120 x 90/100
=shs.108 - log v = n lop p + log a
log a = -1.8
a = 0.01558
n = -1.8 - 0 = 0.6
0 - 3 - amplitude = 2
period = 360/1/2 = 720
phase angle = 30º 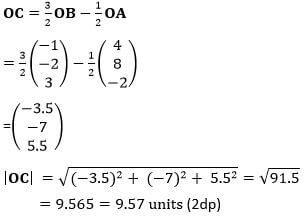
-
- PAYE = 5000 _(3944)
= ksh 1056 - gross tax = 1056 + 1056 = ksh 2112
SLABS
9680 x 10/100 = 968
= 1144
x x 15/100 = 1144
x = 1144/0.15 = 7626.67
monthly income = 9680 + 7626.67 = ksh.17306.7
- PAYE = 5000 _(3944)
- <OAC = <OCA = 70 and OAB = 10
<CAB = 70 + 10
=80º -
-
- AB = -a + b
- CB = 1/3a - 3b
- CM = k(1/3a - 3b)
AM = h (-a + b)
AM = -a + 3b + k (1/3a - 3b)
AM = (-1 + 1/3k) a + (3 - 3k)b
therefore - ha + hb = (-1 + 1/13k)a + (3 - 3k)b
comparing coefficients
-1 + 1/3k = h
3 - 3k = h
hence -1 + 1/3k = 3 - 3k
k = 3/4 and h = 3/4 - OM = -a + 3b + 3/4(1/3a - 3b) = 1/4a + 3/4b
MN = 3/4a - 3/4b - 1/2a + 3/2b = 1/4a + 3/4b
therefore OM = MN hence OM is parallel MN and M is a common point hence O, M and N are collinear.
-
-
mean = -400/110 + 57class f Mid-point (x) x - A = d fd d2 fd2 40-44 3 42 -15 -45 225 675 45-49 30 47 -10 -300 100 3000 50-54 29 52 -5 -145 25 725 55-59 33 57 0 0 0 0 60-64 13 62 5 65 25 325 65-69 1 67 10 10 100 100 70-74 1 72 15 15 225 225 110 -400 5050
= 53.364-
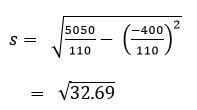
= 5.718 - 50th student
= 49.5 + 17/29 x 5
= 49.5 + 2.9310
=52
-
-
- T3 = a + 2d
T9 = a + 8d
T25 = a + 24d
a + 24d = a + 8d
a + 8d a + 2d
a2 + 16ad + 64d2 = a2 + 24ad + 48d2
16ad + 64d2 = 26ad + 48d2
16d2 - 10ad
16d - 10a = 0 ......... (i)
a + 6d + 2(a + 5d) = 78
a + 6d + 2a + 10d = 78
3a + 16d = 78 .......................(ii)
3a + 16d = 78
16d - 1=a = 0
13a = 78
a = 6, d = 3.75
iii) . a = 6 + 7.5 = 13.5
r = 36/13.5 = 22/3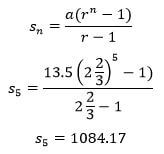
- T3 = a + 2d
-
-
- distance = θ/3602πR cos σ
θ = 29 + 31 = 60º
= 60/360 x 2 x 22/7 x 6370 cos 60
= 33362/3 km or 3336.67 km - time differernce = 4 x 60 = 240 minutes = 4 hrs
local time = 1200h + 4 hrs
= 1600hr or 4:00pm
- distance = θ/3602πR cos σ
- distance = θ 2πR
360
θ/360 x 2 x 22/7 x 6370 = 8000
1001/9θ = 8000
θ = 71.93
71.92 - 60 = 11.93º
B(11.93ºS, 45ºE)
-
-
X
0°
30°
60°
90°
120°
150°
180°
210°
240°
270°
300°
330°
360°
-cos x
-1
-- 0.87
-0.5
0
0.5
0.87
1
0.87
0.5
0
-0.5
-0.87
-1
Sin ( x - 30°)
-0.5
0
0.5
0.87
1
0.87
0.5
0
-0.5
-0.87
-1
-0.87
-0.5
-
- x = 150º, 330º
- x = 120º, 240º
-
-
- P (only one hits
= (2/5 x 3/4 x 4/7) + (1/4 x 3/5 x 4/7) + (3/7 x 3/4 x 3/5)
= 6/35 + 3/35 + 27/140 = 9/20 - P(all hits = 2/5 x 1/4 x 3/7 = 3/70
- P (none hits) = 3/5 x 3/4 x 4/7 = 9/35
- P(two hits) = (2/5 x 1/4 x 4/7) + (1/4 x 3/7 x 3/5) + (2/5 x 3/7 x 3/4)
= 8/140 + 9/140 + 18/140 = 1/4 - P(atleast one hit target) = 1 - P (nonehits the target)
= 1 - 9/35 = 26/35
- P (only one hits
-
- Length of line QS = √(162 + 122) = √400
= 20cm - Height of the pyramid = √(132 - 102) = √69
= 8.3 cm (1 d.p)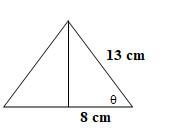
- cos θ = 10/13 = 0.7692
θ = 39.72º - h = √(132 - 62) = 11.53 cm
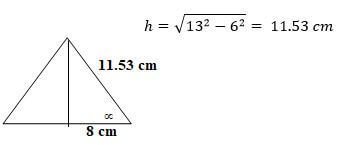
cos σ = 8/11.53 = 0.6938
= 47.06º
θ = 2 x sin-1 (8/11.53)
2 x 43.93
= 87.87º
- Length of line QS = √(162 + 122) = √400
Download Mathematics Paper 2 Questions and Answers - MECS Pre Mock Exams 2023.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students
