Mathematics Paper 2 Questions and Answers - Form 3 End Term 2 Exams 2022

QUESTIONS
SECTION A : 50MKS.

1. Use mathematical tables to evaluate: (4mks)
   3√0.8423 x 72.5
            930.5
2. After how many y years would kshs. 15000 amount to ksh 24015.50 at a rate of 16% p.a. (3mks)
3. Three years ago, Juma was three time as old as Ali. In two years time, the sum of their ages will be 62. Determine their present ages. (3mks)
4. Evaluate:
   ¹/₃ of (2 ¾ - 5 ½ ) x 3⁶/₇ ÷ ⁹/₄ (3mks)
5. Find the height of an isosceles triangle if the equal sides are each 26cm and the base is 48cm long. (2mks)
6. A straight line L1 has a gradient of – ½ and passes through the point P( -1, -3). Another straight line L2 passes through the points Q( 1,-3) and R (4,5), find:
   1. The equation of L1. (2mks)
   2. The equation of L2. (2mks)
7. Solve the following quadratic equation by completing the square. (3mks)
   2x² – 5x + 3 =0
8. Make A the subject of the formula. (3mks)
   T= 2m√L - A
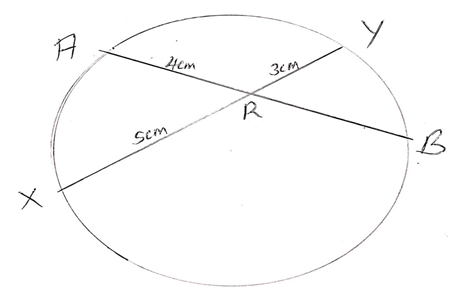
          n     3K
9. In the figure below, chords AB and XY interest in a circl at R. Given that AR = 4cm, XR = 5cm and RY=3cm. find AB. (2mks)
   
10. Given the matrix 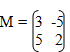 Find the inverse of M and hence or otherwise, solve the   simultaneous equations. (3mks)
    3x – 5y = -9
    5x – 2y = 16
11. Solve the equation   2    -  1     = 1 (3mks)
                                   x-1    x +2     x
12. Solve for x in the equation: (3mks)
    Log (x-1) = log 12 – log (x-2)
13.      
    1. Using binomial expression, expand and simplify ( 1 – 2x)³ up to the term x³. (1mk)
    2. Use the simplified expansion in (a) above to calculate to 4 decimal places the approximate value of (0.98)³ (3mks)
14. A trader bought two brands of sugar labeled Grade A and Grade B. Grade A sugar costs sh 60 per kg and grade B sugar costs sh 50 per kg. he mixed them in a ratio such that after selling the mixture at sh 81 per kg, he made a profit of 50%. Determine the ratio in which he mixed grade A sugar to grade B. (3mks)
15. A quantity P is partly constant and partly varies as the square of Q when Q=2, P= 40 and when Q=3 P=65. Determine the value of P when Q=4. (3mks)
16. A cold water tap can fill a bath in 6 minutes while a hot water tap can fill it in 12 minutes. The drainage pipe can empty the bath in 8 minutes. All the three are opened fully for 3 minutes and then the hot water tap is closed. How many more minutes will it take to fill the bath? (4mks)

SECTION B (50 MKS)
Answer any five questions in this section.

17. Personal tax relief p.a is sh 12672 p.a
    

    Income (K£per annum)	Rate (Sh per pound)
    1-5808	2
    5809-11280	3
    11281-16752	4
    16753-22224	5
    Excess over 22224	6

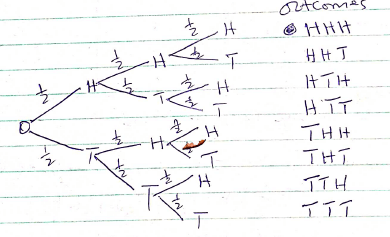
    Mr. Omondi earns a basic salary of sh 15000 per month. In addition, he gets a medical allowance of sh 2400 and a house allowance of sh 12000. Use the tax brackets above to calculate the tax he pays in a year. (10mks)
18. A student at Anestar school tossed a coin three times and recorded the results on every successive toss.
    1. By use of a tree diagram, show all the possible outcomes. (3mks)
    2. Find the probability of getting:
       1. One head (1mk)
       2. Two heads and a tail, in the order. (1mk)
       3. Two heads and a tail, in any order. (1mk)
       4. Three heads. (1mk)
       5. At least one head. (1mk)
       6. No head. (2mks)
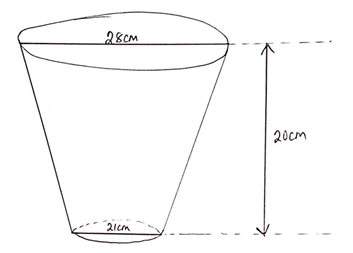
19. The diagram below shows a frustrum made by cutting off a small cone on a plane parallel to the base of the original cone. The frustum represents a bucket with the open – end diameter of 28cm and the bottom diameter of 21cm. The bucket is 20cm deep as shown. Calculate to one decimal place, the capacity of the bucket in litres. (10mks)
    
20. Town B is 180km on a bearing of 050º from town A. another town C is on a bearing of 110º from town A and on a bearing of 150º from town B. A fourth town D is 240km on a bearing of 320º from town A. using a scale drawing 1cm to represent 30km, calculate to the nearest kilometer:
    1. The distance AC (2mks)
    2. The distance CD (2mks)
    3. The distance BC. (2mks)
21. In the figure below OPQ is a triangle in which OS= ¹/₃ OP and OR = ¹/₃OQ. T is a point on QS such that QT = ¾ QS.
    
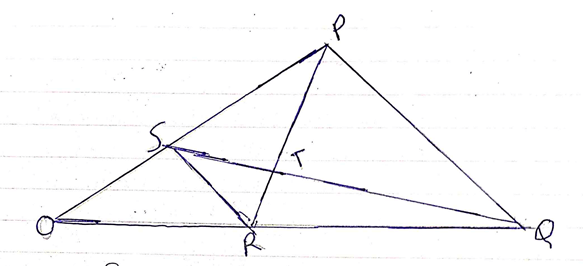
    1. Given that OP = p and OQ=q, express the following vectors in terms of p and q.
       1. SR (2mks)
       2. QS (2mks)
       3. PT (2mks)
       4. TR (2mks)
    2. Hence or otherwise show that the points P,T and R are collinear. (2mks)
22. The first term of an arithmetic progression is 2, the sum of the first 8 terms of the AP is 240.
    1.             
       1. Find the common difference of the AP. (2mks)
       2. Given that the sum of the first n terms of the AP is 1560, find n. (2mks)
    2. The 3rd, 5th and 8th term of another AP form the first three terms of a G.P if the common difference of the AP is 3. Find
       1. The first term of G.P (4mks)
       2. The sum of the first 9 terms of the GP to 4 s.f (2mks)
23. James is a sale executive earning a salary of ksh. 20,000 and commission of 8% for the sales in excess of kshs. 100,000. If in January 2010 she earned a total of ksh. 48,000 in salaries and commissions.
    1. Determine the amount of sales he made in the month. (4mks)
    2. If the total sales in the month of February and March increased by 18% and they dropped by 25% respectively. Calculate:
       1. James’s commission in the month of February. (3mks)
       2. His total earning in the month of March. (3mks)
24. At the beginning of the year 2000, Gachago bought two houses, one in Thika and another one in Nakuru each at sh. 1,240,000. The value of the house in Thika appreciated at a rate of 12% p.a.
    1. Calculate the value of the house in Thika after 9 years to the nearest shillings. (2mks)
    2. After n years, the value of the house in Thika was 2,741,245 while the value of the house in Nakuru was 2917231.
       1. Find n (4mks)
       2. Find the annual rate of appreciation of the house in Nakuru. (4mks)

MARKING SCHEME

1. 
   

   No	Std	Log
   0.8423 72.5 930.5 0.4033	8.423 x 10-1 7.25 x 101 9.305 x 102  4.033 x 10-1	1.925 + 1.8603  1.7858 - 2.9687 2.8171 2.8171 = 3 + 1.8171     3                    3  -1.6057

2. r = ¹⁶/₄ = 4%
   n = ?
   p = 15,000
   A = 24,015 - 50
   A =P(1 + ^r/₁₀₀)ⁿ
   -24015.50 = 15000(1 + ⁴/₁₀₀)ⁿ
      15000       15000
   1.60103 = (1 - 04)ⁿ
   log(1.60103) = nlog1
   n = log1.60103
            log1.021
   n = 12.00 = ¹²/₄ = 3years
3.                  Juma        Ali
   3 yrs ago     3x            x
   Now         3x + 3      x + 3
   2yrs time  3x + 5      x + 5
   x + 5 + 3x + 5 = 62
   4x + 10 = 62
   4x + 10 = 62 
   4x = 62 - 10
   4x = 52
    4      4
   x = 13
   Ali = 13 + 3 = 16yrs
   Juma = 39 + 3 = 42yrs
4. ¹¹/₄ - ¹¹/2 = 11-22 = -¹¹/₄
   ¹/₃x -¹¹/₄ = -¹¹/₁₂
   ²²/7 x ⁴/₉ = ¹²/₇
   -¹¹/₁₂ x ¹²/₇ = -¹¹/₇
5. h = √26² - 24² = 10cm
6.            
   1. y--3 = -½
      x--1 
      2y = -x - 7
      y = ^-x/₂ - ⁷/₂
   2. m² = 5--3 = 8 
      4 - 1
      ⁸/₃ = y - 5
      x - 4
      8x - 32 = 3y - 15
      y = ⁸/_3x - ¹⁷/₃
7. x² -⁵/_2x + ³/₂ = 0
   x² - ⁵/_2x + (⁵/₄)² = -³/₂ + ²⁵/₁₆
   (x -⁵/₄)² = -24 + ²⁵/₁₆ = ¹/₁₆
   x = ⁵/₄ ± ¼
   = ⁴/₄ or ⁶/₄
   x = 1 or ³/₂
8. 3nT² = 4m² . L - A x 3k
                n²         3k
   -A =3n²kT² - L
           4m²
   A = L - 3n²KT²
                 4m²
9. Let RB = X cm
   4 x x = 5 x 3
   4x = 15
   x = 3.75cm
   AB = AR + RB
   AB = 4 + 3.75
   = 7.75cm
10.    
    
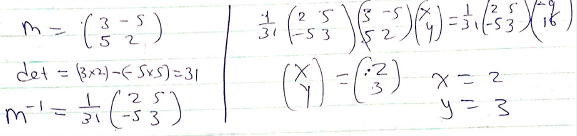
11. 2(x + 2) -1(x - 1) = 1/x
           x² + x - 2
    x² (2x + 4 - x + 1)
    = x² + x - 2
    x² + 5x = x² + x - 2
    4x = -2
    x = -½
12. log(x - 1) = log12 - log(x - 2)
    logx - 1 = log(¹²/_x-2)
    (x - 2)(x 1- 1) = ¹²/_x-2x x -2
    x2 - 3x + 2 = 12
    x2 - 3x - 10 = 0
    (x - 5)(x + 2) = 0
    x = 5
13.         
    1. (1 - 2x)⁵ = 1 - 5(2x) + 10(2x)² - 10(2x)³
       = 1 - 10x + 40x² - 80x³
    2. x = 0.01
       1 - 2(0.01)⁵ = 1 - 10(0.01) + 40(0.01)² - 80(0.01)³
       = 1 - 0.1 + 0.004 - 0.00008
       = 0.9039
14. Let cost price = 100%
    Sellingprice = cp + profit
    = 150%
    150% = 81
    1% = 81/150
    ⁸¹/₁₅₀ x 100 = sh54 per kg
    =60 - 54 = sh6
    =54 - 50 = sh4
    A:B = 1:n
    4n = ⁶/₄
    n = ³/₂
    = 1:³/₂
    2:3
15. P = L + KQ² where K and L are constants
    40 = L + K.22 and 65 = L + K.32
    L + 4K = 40
    L + 9K = 64
    ^5K/₅ = ²⁵/₅
    K = 5
    L + (4 x 5) = 40
    L = 20
    P = 20 + 5Q²
    When Q = 4
    P = 20 + 5 x 4²
    = 100
16. In one minute 
    6/6 + 1/12 - 1/8 = 1/8
    im 3min 1/8 x 3 = 3/8
    remaining 5/8
    1/6 - 1/8 = 1/24
    5/8 ÷ 1/24
    = 15minutes

SECTION II

17. Taxable income per month = sh(15000 + 2400 + 12000)
    = 29400
    p.a = 29400 = ¹²/₂₀
    = K£17640
    Tax due 
    5808 x 2 = 11616
    5472 x 3 = 16416
    5472 x 4 = 21888
    888 x 5 = 4440
    = sh 54360
    less personal relief sh 12672
    = sh41688
18.    
    1.      
       
    2.      
       1. P(one head) = P(HTT) + P(THT) + P(TTH)
          1/8 + 1/8 + 1/8 = 3/8
       2. P(two heads & a tsil in that order) = P(HHT)
          =½ x ½ x ½ = 1/8
       3. P(two heads and a tail in any order)
          = P(HTT) + P(HTH) + P(THH)
          = 1/8 + 1/8 + 1/8 = 3/8
       4. P(three heads) = P(HHH)
          =½ x ½ x ½ = 1/8
       5. P(no head) = P(TTT)
          = ½ x ½ x ½ = 1/8
19. Let height of small cone = h
    then height of large cone = h + 20
    h + 20 = ¹⁴/_10.5 = ⁴/₃
    3h + 60 = 4h
    h = 60cm
    height of small cone = 60cm
    height of large cone = 80cm
    Volume = Vol of large cone - Vol of small cone
    = ¹/₃π(14 x 14 x 80 - 10.5 x 10.5 x 60)
    =¹/₃ x 22/7 x 7 x 7 x 20(2 x 2 x 4 - 1.5 x 1.5 x 5)
    = 22 x 140 x 9.25 litres
           3 x 1000
    = 9.5 litres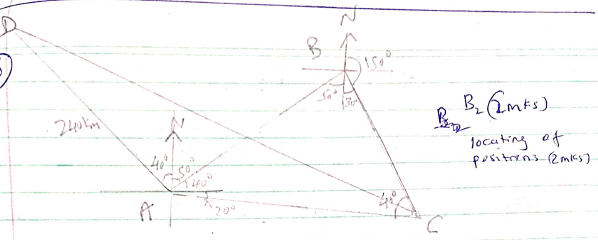
20. 
          
    1. AC = 276KM
    2. CD = 499KM
    3. BC = 243KM
21.      
    1.           
       1. SR = SO + OR
          = -¹/₃P + ¹/₃q
          = ¹/₃(q - p)
       2. QS = QO + OS
          = q + ¹/₃p
          =¹/₃p - q
       3. PT = PS + ST
          -²/₃p - ¼QS
          -²/₃p - ¼(¹/₃p - q)
          -²/₃p - ¹/₁₂p +¼q
          =¼(q - 3p)
       4. TR = TS + SR 
          ¼QS + SR
          ¼(1/3p - q) + ¹/₃(q - p)
          ¹/₁₂p - ¼q + ¹/₃q - p
          = ¹/₁₂(q - 3p)
    2. ¼(q - 3p) = ¹/₁₂(q - 3p)
       hence PT = 3TR = PT//TR
22. s₈ = ⁿ/₂(2a + (n-1)d)
    1.      
       1. 240 = ⁸/₂(2 x 2) + (8 - 1)d
          240 = 4(4 + 7d)
          240 = 16 + 28d
          d = 8
       2. 2 x 1560 =  ⁿ/₂ (2 x 2) + (n - 1)8
          3120 = n(4 + 8n - 8)
          2n² - n - 780 = 0
          n = 40terms
    2.     
       1. a+2d, a+4d, a+7d,.......
          a+4d = a+7d
          a+2d    a +4d
          a² + 8ad + 16d² = a² + 9ad + 14d²
          16d²- 14d² = 9ad - 8ad
          2d²= ad
           d      d 
          a = 6
          first term GP = 12
       2. C.R = ¹⁸/₁₂
          Sn = a(rⁿ - 1)
                       r - 1
          s₉ = 12(1.5⁹ - 1) = 898.6
                       1.5 - 1
23.       
    1. BS = 20000 
       c = ⁸/₁₀₀x
       Jan2010 = 48000
       48000 - 20000
       commission = sh28000
       28000 = ⁸/₁₀₀x
       ¹⁰⁰/₈ x 28000 = 350,000
       350000 + 100000
       = =sh450000
    2.      
       1. 450000 x ¹¹⁸/₁₀₀
          = 531000
          C = ⁸/₁₀₀ x (531000 - 100000)
          ⁸/₁₀ x 431000
          c = sh34480
       2. 531000 x ⁷⁵/₁₀₀ = 398250
          = 398250 - 100000
          = ⁸/₁₀ x 298250
          c = 23860 + 20000
          =sh43860
24.      
    1. A = P(1 + ^r/₁₀₀)ⁿ
       1240000(1 + ¹²/₁₀₀)⁹
       1240000 x 2.773
       = sh 3438.618
    2.              
       1. 2741.245 = 1240000(1 + ¹²/₁₀₀)ⁿ
          2.211 = 1.12ⁿ
          log2.211 = log1.12ⁿ
          log2.211 = nlog1.12
          n = 0.3445
                0.0492
          n = 7yrs
       2. 2917231 = 1240000(1 + ^r/₁₀₀)⁷
          2.3526 = (1 + ^r/₁₀₀)⁷
          7√2.3526 = 1 + ^r/₁₀₀
          1.13 - 1 = ^r/₁₀₀
          0.13 = ^r/₁₀₀
          r = 13%p.a