INSTRUCTIONS TO THE CANDIDATES
- Write your name and index number in the spaces provided above
- This paper contains two sections; Section A and Section B
- All workings and answers must be written on the question paper in the spaces provided below each question.
- Marks may be given for correct working even if the answer is wrong.
- Show all the steps in your calculations, giving your answers at each stage in the spaces below each question.
- This paper consists of 15 printed pages.
- Candidates should check carefully to ascertain that all the pages are printed as indicated and no questions are missing.
Section A. (50mks)
Answer all the questions in this section in the spaces provided.
- Find the value of x that satisfies the equation. (3mks)
log (2x-11)- log2= log3 - log x - The base and the height of a right angled triangle were measured as 6.4cm and 3.5cm respectively. Determine to 1 decimal place the percentage error in calculating the area of the triangle. (3mks)
- The figure below shows a quadrilateral ABCD in which AB = 8cm, DC =12cm <BAD= 45º <CBD= 90º and <BCD =30º
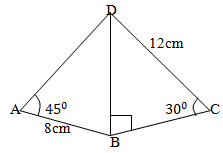
- The length of BD. (1mk)
- The size of angle ADB . (2mks)
- Simply the expression√48/√5+√3 leaving the answer in the form a√b+c where a, b and c are integers. (3mks)
-
- Expand (1+x)7 up to the 4th term (1mk)
- Use the expansion in part (a) above to find the approximate value of (0.94)7 to 3 decimal places. (2mks)
- A variable P varies directly as t3 and inversely as the square root of S. When t=2 and S = 9 P= 16. Determine the equation connecting P, t and S hence find P when S = 36 and t = 3. (3mks)
- Given that
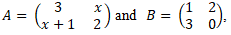 Find the values of x for which AB is a singular matrix. (4mks)
Find the values of x for which AB is a singular matrix. (4mks) - Use completely the square method to solve
3x2+8x-6=0 Correct to 3 significant figures. (3mks) - In the figure below the tangent ST meets chord Vu. Produced at T. chord SW passes through the centre O of the circle and intersect chord Vu at x. Line ST = 12cm and uT= 8cm
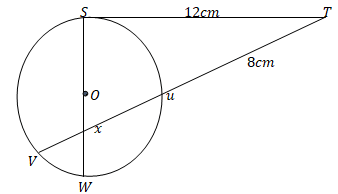
- Calculate the length of chord Vu. (1mk)
- If wx = 3cm and Vx:xu = 2:3 . find Sx
- Make n the subject of the formula.
r/P = M/√n-1 (2mks) - The equation of a circle is given by x2+4x+y2-2y-4=0. Determine the centre and radius of the circle. (3mks)
- The 5th term of an AP is 82 and the 12th term is 103.
Find- The first term and the common difference. (2mks)
- The sum of the first 21 terms. (2mks)
- Use matrices to solve the simultaneous equation. (3mks)
2x+3y=39
5x+2y=81 - Solve the following pair of simultaneous inequalities and illustrate the value on a number line. (3mks)
3x-1 >-4
2x+1 ≤7 - A triangle has sides 10cm, 7cm and 9cm. find
- The area. (2mks)
- The size of angle <BAC. (2mks)
- A plot of land is valued at sh 1,250,000 due to increase in demand its appreciates at the rate of 6% every six months. What will be its value after 3 ½ years. (3mks)
Section B (50mks)
Answer any five questions from this section on the spaces provided. - In a mixed school there are 420 boys and 350 girls. The probability that a girl passes her exams in the school is 4/7 while that of a boy passing is 5/8. The probability of a girl being made a prefect is 2/11 while that of a boy is 1/8.
- Find the probability that a student picked at random.
- Is a boy and passes the exam and is not a perfect. (3mks)
- Is a girl, a prefect and passes the exam. (3mks)
- Is not as prefect and passes the exam. (4mks)
- Find the probability that a student picked at random.
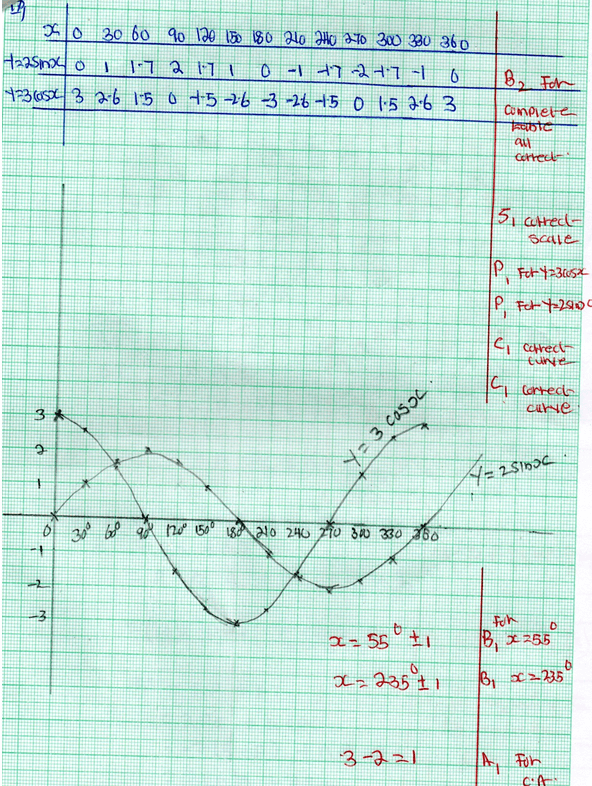
- The table below shows some values of the curves.
y=2 sinx and y=3 cosx- Complete the table for the values of y=2 sinx and y=3 cosx correct to 1 decimal place. (2mks)
xº 0º 30º 60º 90º 120º 150º 180º 210º 240º 270º 300º 330º 360º y=2 sinx 0 1 2 1 0 -1 -1.7 0 y=3 cos3 3 1.5 0 -2.6 -1.5 3 - On the grid below draw the graph of y=3 cosx and y=2 sinx for 0º ≤x ≤360º (5mks)

- Use the graph to find the values of x when 3 cos3-2 sinx=0 (2mks)
- Find the difference in amplitude of y=3 cosx and y=2 cosx (1mk)
- Complete the table for the values of y=2 sinx and y=3 cosx correct to 1 decimal place. (2mks)
- In the figure below , OP = P ,OQ = ⏟q PQ∶ QR =1:1 and OQ: QS = 3:1
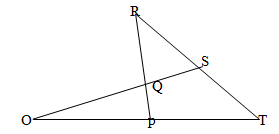
- Determine, in terms of P and q
- PQ (1mk)
- RS (2mks)
- If RS:ST = 1:K and OP:PT = 1:n
Determine.- ST in terms of P, q and K. (2mks)
- The values of K and n. (5mks)
- Determine, in terms of P and q
- Using a ruler and a compass only construct.
- Triangle PQR such that PQ = 6cm , <PQR = 60º and <RPQ = 45º (4mks)
- Locate the point A in the triangle when is equidistant from all the three sides of triangle PQR. (3mks)
- Find the distance of A from the sides of the triangles. (1mk)
- Drop a perpendicular height to PQ and Measure its height. (2mks)
- The figure below represents a cuboids EFGHJKLM in which EF= 40cm FG=9cm and GM= 30cm. N is the midpoint of LM.
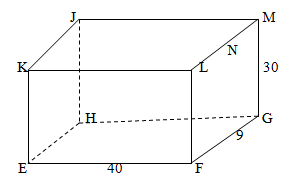
Calculate correct to 3 significant figures- The length of GL. (2mks)
- The length of FJ. (3mks)
- The angle between EM and the plane EFGH. (3mks)
- The angle between the planes EFGH and ENH. (2mks)
- The table below shows income tax rates for a certain year.
A monthly tax relief of Khs 1172 was allowed. Opunyi’s taxable income in the last band was Ksh 3,200 in month.Monthly income in Kshs Tax rate in each shillings 1 – 9400 10% 9401 – 18000 10% 18001 – 26600 20% 26601 – 35600 25% 35601 –and above 30% - Calculate
- His taxable income per month. (2mks)
- The amount of tax he paid in a month. (5mks)
- Opunyi’s salary included a medical allowance of Shs 8000. He contributed 6% of his basic salary to a sacco. Calculate his net pay. (3mks)
- Calculate
- The masses of 100 patients in a hospital were distributed as shown in the table below.
Mass (Kg) 0-9 10-19 20-29 30-39 40-49 50-59 60-69 70-79 80-89 90-99 Frequency 3 7 8 9 12 18 25 10 6 2 - State the modal class. (1mk)
- Calculate
- The mean mass of the patients. (3mks)
- The standard deviation of the distribution. (3mks)
- Find the interquartile range for the data. (3mks)
- OABC is a parallelogram with vertices O (0, 0) A (2, 0) B (3, 2) and C (1, 2).
O1 A1 B1 C1 is the image of OABC under transformation matrix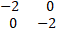
- Find the co-ordinates of O1 A1 B1 C1. (2mks)
- On the grid provided draw OABC and O1 A1 B1 C1 (2mks)
- Find O11 A11 B11 C11 the image of O1 A1 B1 C1 under the transformation matrix
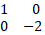 (2mks)
(2mks)- On the same grid draw O11 A11 B11 C11 . (1mk)
- Find the single matrix that map O11 A11 B11 C11 onto OABC. (3mks)

MARKING SCHEME
- log(2x-11)- log2= log3- logx
2x-11/2 = 3/x
x(2x-11) = 6
2x2 – 11x – 6 = 0
2x2 – 12x + x – 6 = 0
2x(x-6) + 1(x – 6) = 0
2x + 1 = 0 x- 6= 0
2x = -1 x =6
X= - ½
M1 for 2x-11/2 = 3/3
M1 for attempting to solve quadritic equation
A1 for both values of x - Actual area
= ½̸ ×6432 ×3.5 =11.2
Limits 6.45 3.55
6.35 3.45
Max area ½ × 6.45 ×3.55 =11.45
Min area ½ × 6.35 ×3.45= 10.93
A.E. A - max- min 11.45-10.95=0.25
2 2
% Error = 0.25/1.2 ×100
= =2.2%
M1 for limits
M1 for ½ ×6.35 ×3.45
A1 for % error 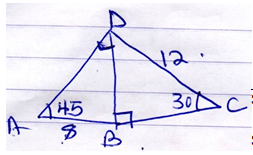
BD = 12
sin30 sin90
BD = 12 × sin30 = 6
sin90
8 = 6
SinADB sin45
SinADB= 8 × sin45
6
= 0.942
ADB = sin-10.942
= 70.39
M1 for expression to find BD
M1 for SinADB= 8 × sin45
6
A1 for % correct Angle- √48 × √5-√3
√5+√3 √5 -√3
√240-√144 = 4√15-12
5-2 3
= 4/3 √15 - 4
M1 for multipying by conjugate
M1 for 5-2
A1 for % C.A -
- (1+ x)7
17xº + x1 – x2 + x3
1 4 6 4
= 1 + 4x + 6x2 + 4x2 - (0.94)7 = (1 + -0.06)7 x = -0.06
1 + 4 (-0.06) + 6( -0.062) + 4 (-0.063)
1 + 0.24 + 0.0036 =1.244
B1 for corrrect expansion
M1 for x= -0.06
A1 for correct value
- (1+ x)7
- P = Kt3
√5
16 = K23
√9
16 × 3= 8 K 16 × -3=K
8 8 8
K=6 K= -6
P = 6t3
√5
P = 6 ×33 = 6 × 27 = 27
√36 6
P = -6 ×33 = -6 × 27 = -27
√36 6
M1 for P = 6 × 33
√3
A1 correct value of P. 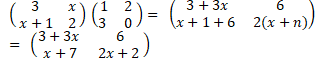
(3+3x)(2x+2) = 6( x+7)
6x+6+6x2+ 6x = 6x+42
6x2+ 12x – 6x + 6 – 42 = 0
6x2 – 6x – 36 = 0
x2 – x – 6 = 0
x2– 3x + 2x – 6 = 0
x( x- 3) + 2( x-3 ) = 0
x+ 2 = 0 x – 3 = 0
x = -2 x = 3
M1 for ( 3+3x)( 2x+2) =6 ( x+7)
M1 for Attempting to solve quadratic equation
A1 for x = -2
A1 for x = 3- 3x2+8x-6=0
x2 + 8/8 x – 6/3=0
x2 + 8/3 x+K=2+K
K=(8/3 ÷2)2= (8/3 ×½ = (4/3)2= 16/9
x2+ 8/3 x + 16/9= 2+ ( 16 )/(9 )
( x+ 4/3)2 =37/9
x+4/3= √37/9 x= -1.944-1.333
x=1.944-1.333 x= -3.277
x=0.611
M1 for x2+ 8/3 x + 16/9= 2+ ( 16 )/(9 )
M1 for x+4/3= √37/9
A1 for both values of x -
- TS2 =8(8+x)
144 = 64 + 8x
80 = 8
10 = x
Vu = 10cm - vx = 4cm (2/5 ×102)
Xu= 10cm – 4 = 6
4×6=3 × x x = 4 x 62 =8cm
3
Sx = 8cm
M1 for 144=64+8x
A1 for C.A
M1 for vx or xu
A1 for 8cm
- TS2 =8(8+x)
- r/p = m/√n-1
r2/p2 = (m2)/(n-1 )
r2 (n-1 )= m2p2
r2n - r2 =m2p2
r2 n =m2p2 +r2
r2 r2
n=m2p2 +r2
r2
M1 for squaring
A1 for C.A - x2+4x+K+y2-2y+K=4
K= (4/2)2=4 K= (-2/2)2=1
x2+4x+4 +y2-2y+1=4+4+1
(x+2)2 + (y-1)2= a
(x-a)2 +(y-b )2= r2
a= -2 b=+1 r=3
M1 for competing the square
A1 for centre
A1 for radius -
- 5th = a+4d=82
12th= a+11d=103
-7=-21
d=3
a+4d=82
a+12=82
a=82-12
= 70 - = n/2( 2a+(n-1)d
= 2½ (2×70+20 ×3)
= 2½ ((140+60)
= 2100
M1 for -7d= -21 (or equivalent)
A1 for term 1
M1 for substitution
A1 for C.A
- 5th = a+4d=82
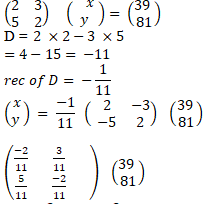
x=-2/11×39+ 3/11×81=15
y= 5/11×39 + -2/11×81=3
M1 for determinant
A1 for correct values of x and y- 3x-1 > -4 2x+1≤7
3x >-4+1 2x≤6
3x > -3 x ≤3
x> -1
- 1 <x ≤3
M1 for 3x > -3
A1 for x ≤3 and x >-1
B1 for number line with correct arrow - Area =P=10+7+9
= 26
S= 13
A = √(13(13-10)( 13-7)(13-9))
=30.5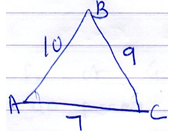
½ ×10 ×7 ×sinBAC=30.5
= sinBAC= 30.5/35
= 0.8714
BAC=60.6
M1 for for substitution of a, b c and S in the formula
A1 Correct Area
M1 for sinθ= 30.5/35
A1 for correct angle - A= P( 1+ r/100 )n
= 1250000 (1+ 6/100)7
=1250000 × 1.067
=1879537.82
M1 for substitution
M1 for (1+ 6/100)7
A1 for Amount -
- B and passes and not prefect
6/11 × 5/8 × 7/8 = 105/352 - G and prefect and pass
5/11 × 2/11 × 4/7= 40/847 - B or G
B NP passes or G NP passes
= 6/11 × 5/8 × 7/8 + 5/11 × 9/11 × 4/7
= 105/352 + 180/847
= 0.5108
M1 for 7/(8 )
M1 for 6/11 × 5/8 × 7/8
A1 for C.A
M1 for 5/11 × 2/11 × 4/7
A1 for C.A
M1 for 6/11 × 5/8 × 7/8 + 5/11 × 9/11 × 4/7
A1 for 105/352
A1 for 180/847
A1 for 0.5108
- B and passes and not prefect
-
-
-
- PQ=PO+OQ
= - P+q - RS = RQ+Q S
= -PQ+ 1/3 OQ
= P- q+ 1/3 q
P - 2/3 q
- PQ=PO+OQ
-
- ST/RS = K/T
ST=KRS
K=(P- 2/3q)
=KP - 2/3 qK - Expressing RT in two ways
RT = RS + ST
= P- 2/3 q+KP- 2/3Kq
=(1+K)P +(-2/3- 2/3 K)q
RT=RP+PT
= 2PQ + nOP
= -2(q- p) + nP
= (2+ n)p – 2q
(1 +K) P + (-2/3- 2/3K)q =(2+n )p-2q
-2/3 - 2/3 K= -2 1 + K = 2+ n
K=2 1+ 2 = 2+ n
1 = n
B1 for PQ
M1 for P- q + 1/3q
A1 for P- 2/3q
M1 for K(P-2/3q)
A1 for correct vector
M1 for P- 2/3 q+KP- 2/3 Kq
M1 for (1 +K) P + (-2/3- 2/3K)q
M1 for equating the two expression
A1 for K
A1 for n
- ST/RS = K/T
-
-
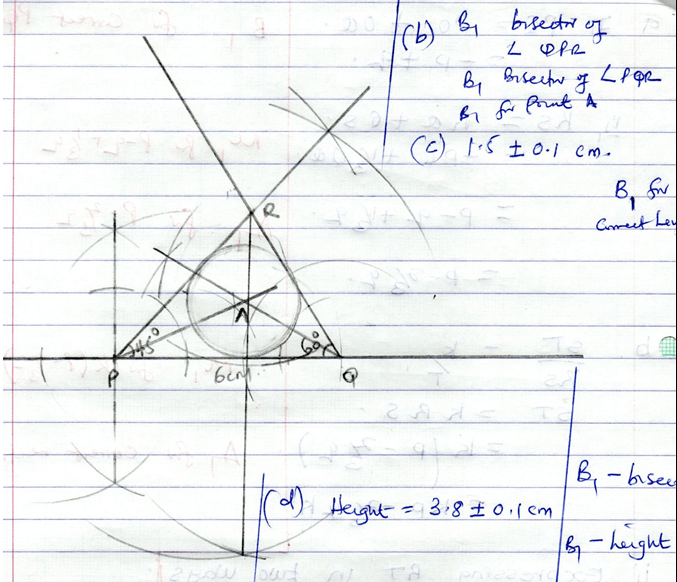
-
- GL2= 92 + 302
GL=31.3 - FJ2 =FH2+ HJ2
FH2 = 40+ 92
FH =HI
FJ2= 412 +302
FJ2= 50.8 - EM and EFGH
EM projection = EG
<GEM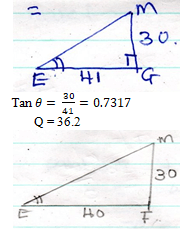
Tan θ = 30/41=0.75
Q = 36.87
M1 for 92 )+ 302
A1 for correct lenght
M1 for FH2=40+ 92
M1 for FJ2= 412 +302
A1 for 50.8
M1 for Tan θ= 30/41
M1 for projution
A1 for Q
M1 for Tan θ
A1 for angle
- GL2= 92 + 302
- Taxable income
= 35600 + 3200
= 38800- 1st 9400 ×10/100=940
Next 8600× 15 /100×8600=1290
Next 8600× 20/100×8600=1720
Next 9000 × 25/100×9000=2250
Next 3200 × 30/100 ×3200=960
(Total tax = & 71 60
less relief 1172 )
Shs 5988 - Basic salary = taxable income – allowances
= 38800 – 8000
Sacco = 6/100 ×30800 = 1848
Net salary = T.1 – (PAYE + Sacco
= 38800 – (5988 + 1848)
= 38800 – 7836
= Ksh 30964
M1 for addition
A1 for 38800
M1 for first slab
M1 for 2nd and 3rd slabs
M1 for last 2 slabs
A1 for gross tax
A1 for Net tax
M1 for 1848
M1 for substration
A1 for C.A
- 1st 9400 ×10/100=940
-
Mass X F Fx dx-x d2 Fd2 x2 Fx2 0-9 4.5 3 13.5 20.25 60.73 10-19 14.5 7 101.5 210.25 1471.75 20-29 24.5. 8 196 600.25 4802 30-39 34.5 9 310.5 1190.25 10712.25 40-49 44.5 12 534 1980.25 23769 50-59 54.5 18 981 2970.25 53464.5 60-69 64.5 25 1612.5 4160.25 104006.25 70-79 74.5 10 745 5550.25 55502.5 80-89 84.5 6 507 7140.25 42841.5 90-99 94.5 2 189 8930.25 17860.5 100 5190 - Modal class
= 60 – 69 -
- (Mean =ƸFx/ƸF = 5190/100 = 51.9
- standard deviation
√ƸFx2/ƸF- (ƸFx/ƸF)2
= 314485/100- 51.92
= 3144.86 – 2696.61
=√448.24
=21.17± 0.1
B1 for Modal class
M1 for ƸFx
M1 for ƸF
A1 for Mean
M1 for 314485/100- 51.92
M1 for Square root
A1 for C.A
- Modal class
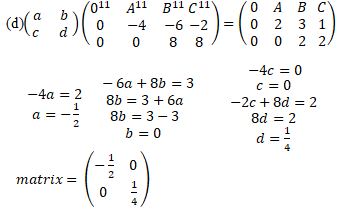
M1 for finding cordinates
A1 for cordinates
B1 for OABC drawn
B1 for O1 A1 B1 C1 drawn
M1 for Attempting to find cordinates
of O11 A11 B11 C11
A1 coordinates of O11 A11 B11 C11
B1 for O11 A11 B11 C11 drawn
M1 for Attempting to find matrix
A1 for a= -½
A1 for matrix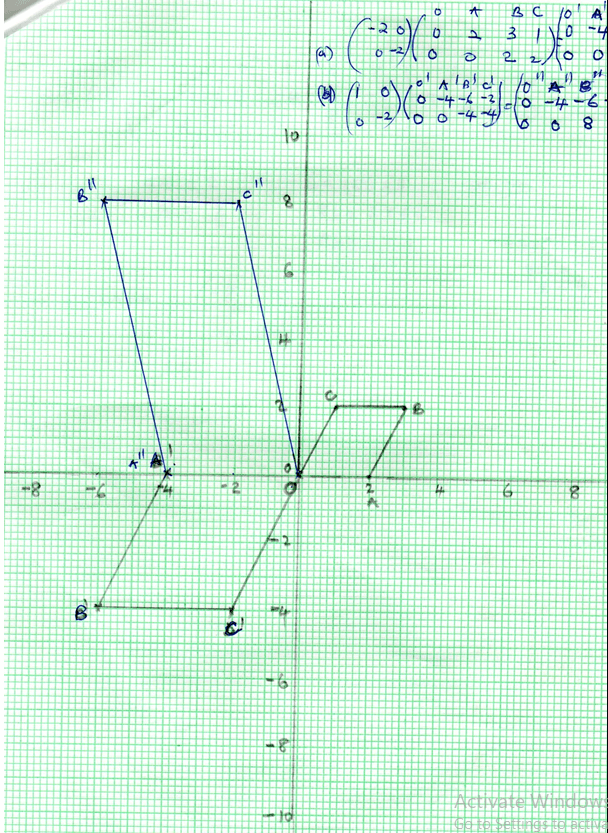
Download Mathematics Paper 2 Questions and Answers - Kangundo Subcounty Pre Mock Exams 2021/2022.
Tap Here to Download for 50/-
Get on WhatsApp for 50/-
Why download?
- ✔ To read offline at any time.
- ✔ To Print at your convenience
- ✔ Share Easily with Friends / Students

